Casimir forces: Still surprising after 60 years
DOI: 10.1063/1.2711635
It might come as a surprise that both the gecko’s ability to walk across ceilings in apparent defiance of gravity and the evaporation of black holes through Hawking radiation can be understood as arising from zero-point fluctuations of quantum fields. The connections can be made thanks to work done at Philips Laboratories in the late 1940s by Hendrik Casimir and collaborators, work described in a series of three papers. 1–3
Almost two decades earlier, Fritz London had used the new quantum theory to derive the attractive force between atoms or molecules without an electric dipole moment; his result represents one of the theory’s early major successes. Before London’s calculation, the van der Waals attraction between polar molecules was understood, but the origin of the experimentally known nonzero van der Waals correction to the gas law for nonpolar gases such as helium was a mystery. London explained the origin of the attractive force between nonpolar molecules or atoms as due to zero-point fluctuations in the positions of their charged constituents.
The basic idea was delightfully presented in Physics Today by Daniel Kleppner (October 1990, page 9
Power failure
The interatomic potential determined by London varies inversely as the sixth power of the separation between the atoms. However, in their experimental work with colloids at Philips Labs in the Netherlands, Theo Overbeek and Evert Verwey observed a different behavior at large distances. The attractive potential between the colloidal particles, assumed to result from the attractions between the individual atoms that the particles comprise, appeared to fall off faster than 1/R 6. Noting that London’s calculation assumed an instantaneous electromagnetic interaction, Overbeek suggested that if the finite velocity of light were taken into account, the van der Waals potential might be modified at large separations. Overbeek approached Casimir (shown in figure 1) and Dik Polder, who together attacked the problem. 1 The two first considered a simpler system, a single atom in an electromagnetic cavity with perfectly conducting walls, and they calculated the atom’s interaction with the nearest cavity wall as a function of separation distance. Using a full zero-temperature quantum electrodynamic treatment of the field in the cavity, they showed that for large separation the atom would be attracted to the wall by a force now called the Casimir–Polder force. Moreover, the energy of attraction has the surprisingly simple form

Figure 1. Hendrik B. G. Casimir (1909–2000), around 1950, when he did his pioneering work on the consequences of electromagnetic zero-point energy.
(Courtesy of American Institute of Physics, Emilio Segrè Visual Archives.)

where c is the velocity of light and α is the static electric polarizability. Casimir and Polder next calculated the energy of attraction between two atoms and found that for two identical atoms,
Casimir and Polder’s calculation is not simple; Evgeny Lifshitz, in a paper that presents an extension of Casimir’s calculation to real materials, and about which more will be said, commented on the calculation’s unwieldiness. 4 But the formulas are simple, and that simplicity inspired Casimir to seek a fundamental explanation. He mentioned his results to Niels Bohr and, he reported, 5 “Bohr mumbled something about zero-point energy.” That remark was enough to lead Casimir to formulate a new approach that allowed him to reproduce the results—previously obtained with much labor—in about two printed pages. 2 In the new approach, Casimir simply assigned a zero-point energy ħω/2 to every mode of the cavity and calculated the net shift in zero-point energy by using the well-known formula for the perturbation of cavity-mode frequencies:
where α is the static electric polarizability of a particle placed at location (x 0, y 0, z 0) in the cavity, E 0(x, y, z) is the unperturbed field, and the integral is over the cavity volume. The energy is formally determined by a sum over all cavity modes, which diverges, but the energy of attraction can be obtained by taking the energy difference for two particle–wall separations. Casimir’s technique reduced a full quantum electrodynamics problem to a simpler classical electromagnetism problem.
Note that “time” does not appear explicitly in the calculations I have discussed, so it would seem that the term “retarded van der Waals” to describe the force modification in the long-distance region is a holdover from Overbeek’s original suggestion. In Casimir’s calculations, as the distance from the wall or the distance between two atoms increases, the contributions from high frequency modes tend to average to zero and only the long-wavelength modes contribute to a coherent sum. However, the calculations can be done with other methods, such as using Green’s functions, and the effect of time delay can be elucidated.
In the final paper of the series, 3 Casimir performs what he calls the “obvious extension” to the force between the cavity walls themselves due to the cavity’s zero-point field and obtains the famous result for the attractive force between two perfectly conducting plates:
where d is the plate separation and A is the plate area. The electron charge does not explicitly appear in Casimir’s formula; the electron’s role as charge carrier is to provide the physical basis for the perfectly conducting boundary condition.
Real materials
Casimir’s conducting-plates paper is among the most important in the history of physics, because it shows that the boundary conditions of a system can affect the zero-point energy of the system and, hence, the system’s properties. The concept has wide application in physics, as attested by the thousands of citations to the paper.
Casimir’s work was first extended by Lifshitz in what stands as a masterpiece of mathematical physics. Lifshitz’s work was done in support of the experimental studies of Boris Derjaguin and Irina Abrikosova, who were investigating the short-range attractive forces between dielectric materials. 6 Lifshitz generalized Casimir’s perfect-conductor calculation by treating the electrodynamic mode boundary problem for real materials. Such an extension was required for two reasons: First, individual atomic or molecular polarizabilities are modified when the atoms or molecules are assembled into a bulk material. Second, as was first suggested by Benjamin Axilrod and Edward Teller, 7 the van der Waals forces are not additive: The presence of a third atom in the vicinity of an interacting pair modifies the two-particle interaction. The most straightforward way to address a real material is to solve the electromagnetic boundary condition.
Note, however, that if the polarizability is determined from the index of refraction by using the textbook Clausius–Mosotti relation, then as the index of refraction approaches infinity, a direct summation of the van der Waals forces between molecule pairs in adjacent plates gives a total force that comes within 20% of the perfectly conducting Casimir result (reference , page 250). The near equality suggests that it is reasonable to approximate the force between colloidal particles by using Hamaker coefficients—that is, pairwise sums of the van der Waals force between molecules—for a specified geometry. In any case, the full mode calculation for the attraction of two dielectric spheres has not been performed to date. The determination of attractive force by pairwise additions breaks down badly when the properties of a high-density material are significantly different from those between the individual atoms or molecules that the material comprises. Such is the case, for example, in fused silica and many other dielectric materials. In those situations, one can treat the system as an electromagnetic-cavity boundary problem, provided that the material’s complex electric permittivity ε(ω) = ε′(ω) + i ε″(ω) is known.
Source of the force
Casimir’s result, equation
Pauli’s initial reaction is not surprising. In his Lectures on Physics, 9 he states, “For radiation the zero-point [energy of the electric field] is not important” (page 75). He had considered the effects of an electromagnetic zero-point energy and came to the conclusion that its gravitational effect would be so enormous that the radius of the universe “would not even reach the moon” (page 115). Pauli’s calculation, which was never published, cuts off the zero-point fluctuation field for wavelengths shorter than the classical electron radius r e, defined by setting the electron’s rest energy equal to the energy of its electrostatic field. The total energy density is given by the sum of the zero-point energy of each mode, ħkc/2, and the mode density is 2 × 4π 2 k 2 dk/(2π)3, where the prefactor 2 accounts for the two polarization states of each mode. Thus the energy density is
Taking k max = 2π/r e and r e = 2.82 × 10−13 cm, one finds ρ E to be about 1014 g/cm3. That is some 1043 times larger than the presently accepted value of the dark-energy component of the universe, 10−29 g/cm3.
Defining the cutoff in terms of the classical radius of the electron is artificial. A more natural cutoff would correspond to the Planck length,
Some light can be shed on the cosmological constant problem by considering Lifshitz’s extension of Casimir’s calculation. In the Lifshitz calculation, fields have no zero-point energy; they are completely classical but coupled to the material. If one Fourier transforms the material’s position fluctuations to obtain a spectral density, at each frequency ω = ck there is a zero-point energy ħω/2 that persists, even at absolute zero. Those material fluctuations, at finite temperature, are responsible for Johnson noise, for example, which is well-known in electronics, and follow from the quantum fluctuation–dissipation theorem. If the real and imaginary parts of the electric permittivity ε(ω) are given for the material that makes up the two flat plates, the allowed modes between the plates can be determined; the imaginary part of ε represents dissipation and thus serves as the source term for the electromagnetic fields between the plates.
The point is that the Casimir force and related forces can be understood without reference to fluctuations of the vacuum itself. For example, Casimir and Polder could have performed their calculation while considering a real material for the cavity walls, one with dissipation. The field excitations would follow the material fluctuations, with ħω/2 being the apparent zero-point energy of each cavity mode, but there would be no field quantization. The alternate point of view just presented raises an issue similar to the historical question as to whether the photoelectric effect or Planck’s treatment of blackbody radiation provides direct proof for the existence of photons: In both of those cases, one cannot decide between quantization of the field and quantization of the field–matter interaction. That is not to say that photons do not exist, but that experimental proof for the quantization of the electromagnetic field must be sought elsewhere.
Remarkably, Sergei Rytov, who is referenced by Lifshitz, and Herbert Callen and Theodore Welton independently and roughly simultaneously developed formalisms along the lines sketched above. Callen and Welton provide the more general treatment. 10 In their view, the vacuum represents a dissipative medium; the quantization occurs in the material, and the vacuum contributes to the imaginary part of the electrical permittivity. Further, it was pointed out by Timothy Boyer that the electromagnetic modes responsible for the Casimir force are not free-space modes but evanescent surface modes of the material. So the existence of the Casimir force really doesn’t say anything about the vacuum of space itself; rather, it speaks to the interactions of materials with their own nearby electromagnetic modes.
The question remains: Does the vacuum of free space contain zero-point energy manifested as a cosmological constant or other kind of dark energy? The modern observations of an accelerating cosmos imply the existence of a dark energy that imbues space. However, given the rather ridiculous zero-point energy associated with the electromagnetic and other fields, one should probably conclude that those fields do not contribute to the dark energy. Rather, the observed energy is an artifact of the way fields interact with matter: The interaction allows the fields to be treated as having a zero-point energy. Of course, that argument is not entirely satisfactory. But it is fair to say that the study of Casimir and related zero-point energy effects doesn’t tell much about the properties of the vacuum of free space, though it can constrain those properties. For example, simply setting k max of the zero-point fluctuations to be small enough to agree with the observed cosmological dark energy would be inconsistent with the experimentally verified Casimir and related forces.
Recent advances
Within a few years of Casimir’s prediction of the attractive force between parallel plates, Marcus Sparnaay performed the first experimental test. His result had roughly 100% uncertainty but conclusively demonstrated a short-range attraction. Until fairly recently, that experiment was the most often quoted experimental proof of the Casimir force. In the years after Sparnaay’s experiment, a number of experiments explored various systems—with metals, dielectrics, ionic fluids in the space between the plates, and so forth. In 1973 Edward Sabisky and Charles Anderson tested the Lifshitz theory by measuring how the vapor pressure of a thin superfluid liquid helium film adsorbed on a freshly cleaved alkaline-earth fluoride crystal varied as a function of film thickness. Their measurements agreed with the theory to within a few percent.
When I began my own experimental work in 1994, as a supervisor of what ended up being a series of undergraduate senior research projects at the University of Washington in Seattle, the most accurate of the experiments between bulk objects had determined the exponent in the Casimir force law to about 20% and obtained a similar precision for the multiplicative coefficient. Our hope was to improve the experimental accuracy, extend the measurements to longer distances, and measure the effects of nonzero temperatures, expected to dominate at distances larger than 4 μm. However, the experimental sensitivity was about an order of magnitude away from being able to detect the finite-temperature correction. I eventually obtained results that could be used to determine the parameters in the force law over a range of distances from 0.6 μm to about 6 μm.
That experiment ended up being a watershed for renewed interest in the subject, both for theory and experiment. It was clear from my work that the finite-conductivity correction obtained by simply treating the metals according to a plasma model is completely incorrect. Astrid Lambrecht and Serge Reynaud performed the first accurate calculation, and after I corrected a 10% calibration error in my experiment, the agreement between their theory and my result was satisfactory. 11
In 2000 Mathias Boström and Bo Sernelius showed that the form of the electric permittivity has a critical effect when one calculates the finite-conductivity correction in combination with the nonzero-temperature correction. 12 In the usual approach, the finite-temperature correction is treated by replacing the zero-point excitation ħω/2 with ħω coth(ħω/2k B T), where k B is Boltzmann’s constant. The latter function has simple poles on the imaginary axis at ħω/2k B T = in π, so the integral over frequency in the Lifshitz formalism is replaced by a sum of the residues of the spectral function at those poles. The dominant contribution comes from the pole at n = 0. Boström and Sernelius assumed the material to have an electric permittivity given by the so-called Drude model and found that the contribution of the n = 0 transverse electric mode vanishes. So, compared with previous calculations in which the transverse electric and transverse magnetic modes had roughly equal contributions, their result shows a large correction to the force at distances of order 1 μm and demonstrates that the force is reduced by a factor of two for large separation.
However, the theoretical story is far from simple. Boström and Sernelius’s result apparently disagrees with a number of experiments and most significantly with my own. Their correction is about as large as the plasma-model corrections that I ruled out. A study of the spectrum of the finite-temperature correction suggests that low frequencies make the dominant contribution; the frequencies are low enough that it might not be possible to describe the response of the metal in terms of a simple Drude-model electrical permittivity.
The principal theoretical issue is that, in the 109 to 1012 Hz range, the electron’s mean free path in a metal can exceed the electromagnetic skin depth. That would lead to nonlocal correlations and imply that the permittivity cannot be described by a simple analytic function. The problem of nonlocal correlations in metals was first addressed in detail in the 1940s by Fritz London’s slightly less famous brother Heinz, but it has yet to be treated in detail in a satisfactory manner.
It is fair to say that finite-conductivity effects and the thermal correction to the Casimir force are experimental questions. My colleagues and I hope to construct a new torsion-balance experiment that will allow accurate measurements at long distances and address those issues. Roberto Onofrio’s group at Dartmouth College is experimentally exploring the thermal correction to the Casimir force; the experiment is shown in figure 2. On the other hand, the finite-temperature correction to the Casimir–Polder force has been measured by Eric Cornell’s group at JILA. Figures 3 and 4 display that experiment, and figure 5 gives the results, which are in good agreement with theory. Unfortunately, the nature of the calculations for the Casimir and Casimir–Polder forces are quite different.

Figure 5. The vibration frequency of a Bose–Einstein condensate in the JILA experiment varied with distance from the fused silicon substrate and with temperature. The vertical axis is the fractional shift in frequency as compared with its asymptotic value. The lab temperature is 310 K. The colored curves give the group’s theoretical calculations, which agree well with the experimental data.
(Courtesy of John Obrecht and Eric Cornell, JILA.)
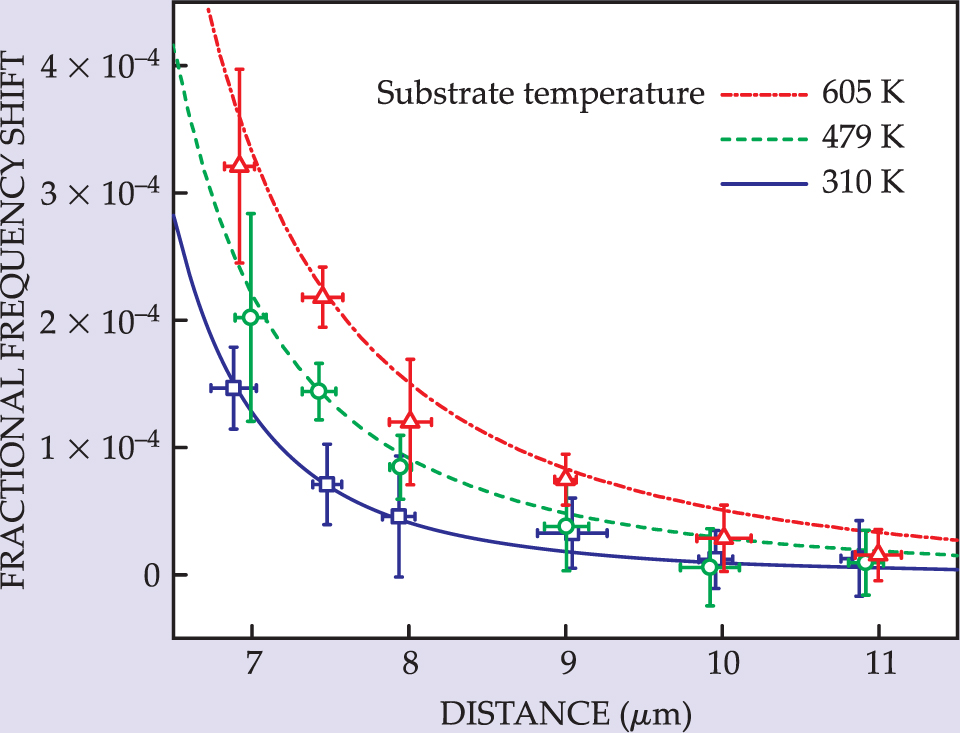

Figure 4. The fused silica substrate, Pyrex holder, and Pyrex chamber are visible in this photograph of the JILA group’s experimental trapping volume.
(Courtesy of John Obrecht and Eric Cornell, JILA.)


Figure 3. The Casimir–Polder force between a Bose–Einstein condensate (BEC) of atoms and a fused silica surface has been measured by Eric Cornell and colleagues at JILA. The gradient of the Casimir–Polder force, which is manifested as an additional harmonic term to the trap potential, affects the vibration frequency of the BEC in the direction perpendicular to the surface. This schematic shows that the BEC is well localized near the fused silica surface. A laser heats the silica and allows for an investigation of the force’s temperature dependence.
(Courtesy of John Obrecht and Eric Cornell, JILA.)
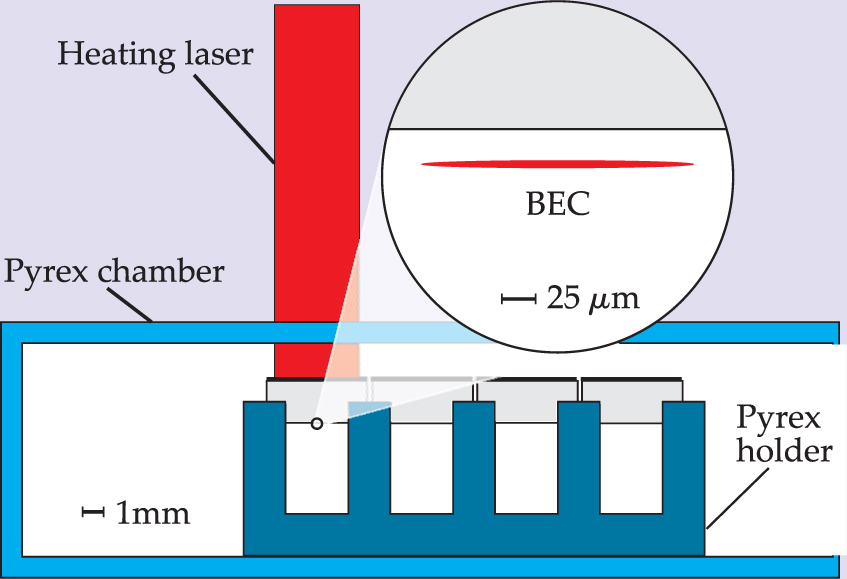

Figure 2. A plane–cylinder geometry is employed in a new Casimir-force experiment under development by Roberto Onofrio and colleagues at Dartmouth College. The plane, a gold-plated silicon wafer 1 cm wide and 200 μm thick, is clamped along one edge between two plates of aluminum and is configured as a mechanical resonator. The vertical white object is an optical fiber used for interferometric distance measurement. In the foreground is the cylinder holder, mounted on a piezoelectric transducer for fine distance control; mechanical actuators provide coarse distance and tilt control. The cylinder, a gold-coated optical-quality cylindrical lens, is 2 cm long and 1 cm wide, with a radius of curvature of 2 cm. A change in the mechanical resonance frequency of the clamped plane will provide a measure of the gradient of the Casimir force. The Dartmouth group hopes to obtain sufficient sensitivity to measure with high accuracy the thermal correction to the Casimir force.
(Courtesy of Michael Brown-Hayes and Roberto Onofrio, Dartmouth College.)

The present state of theory and experiment has been reviewed in a special edition of the New Journal of Physics. 13 In particular, Onofrio reviews the status of the most accurate experiments, with an eye toward understanding the feasibility of looking for new long-range forces that might extend some microns from a material surface. Those forces are associated with corrections to Newton’s law, and their existence is suggested by string theory.
The desire to test for such forces strongly motivates a fuller theoretical understanding of corrections to the Casimir force: The effects of oxide coating, absorbed water, absorbed hydrogen, roughness—essentially an endless list—all need to be addressed. It may not be possible to calculate the force to better than 10% for plate separations less than 1 μm, mostly because the material properties cannot be known to sufficient accuracy. It likely is possible to perform highly accurate calculations for large plate separations, for which the Casimir force becomes small and the material properties less important. Still, the lower distance-range limit of tests for new forces would be restricted. Some techniques have been proposed to get around these problems, most notably placing a conducting shield between the two plates. That would allow the position of one plate to be varied without affecting the electromagnetic modes between the shield and the other plate. Of course, the shield’s introduction presents an interesting experimental alignment problem, and it is unlikely that such a shield could be implemented for distance ranges significantly less than 1 μm; the shield needs to be thick enough to be effective.
Applications
One of the first applications of the Casimir force was Casimir’s own attempt to derive the fine structure constant α. His idea 8 was to model the electron as a conducting sphere of radius r e. The associated zero-point energy comes primarily from frequencies near c/r e, so the energy can be estimated as
where C is a dimensionless constant that, if positive, implies an inward force. That inward force balances the outward Coulomb force when the magnitudes of the corresponding energies are equal: e 2/2r e = Cħc/2r e. Thus, e 2/ħc = α = C and is independent of the radius. A detailed calculation of C by Boyer, however, shows that Casimir’s intuitive approach was off the mark: The constant is negative, equal to about −0.09; that is, the stress on a conducting sphere tends to make it expand. Boyer’s result remains of interest because it highlights the geometry dependence of the Casimir force, a subject that has received considerable attention.
When one considers the acceleration of conducting plates in a cavity, new physics comes into play that is related to the evaporation of black holes. The so-called dynamical Casimir effect posits that photons can be generated when the plates are accelerated toward each other. The effect is closely related to the Unruh–Davies effect, 8 which an accelerated detector appears as immersed in a thermal blackbody radiation bath with temperature
where a is the acceleration. The Unruh–Davies effect can be roughly understood by considering a virtual photon that propagates away from an accelerated object. When the photon returns some time later, its energy is no longer equal, in the accelerated frame, to its value when it left the object; detailed calculation shows that its energy increases. It is tempting to invoke the equivalence principle and assign the temperature defined by equation
On the other hand, when equation
A more practical application of the Casimir and related forces is to the wetting of surfaces by liquids. (For an introduction to wetting, see the Quick Study on
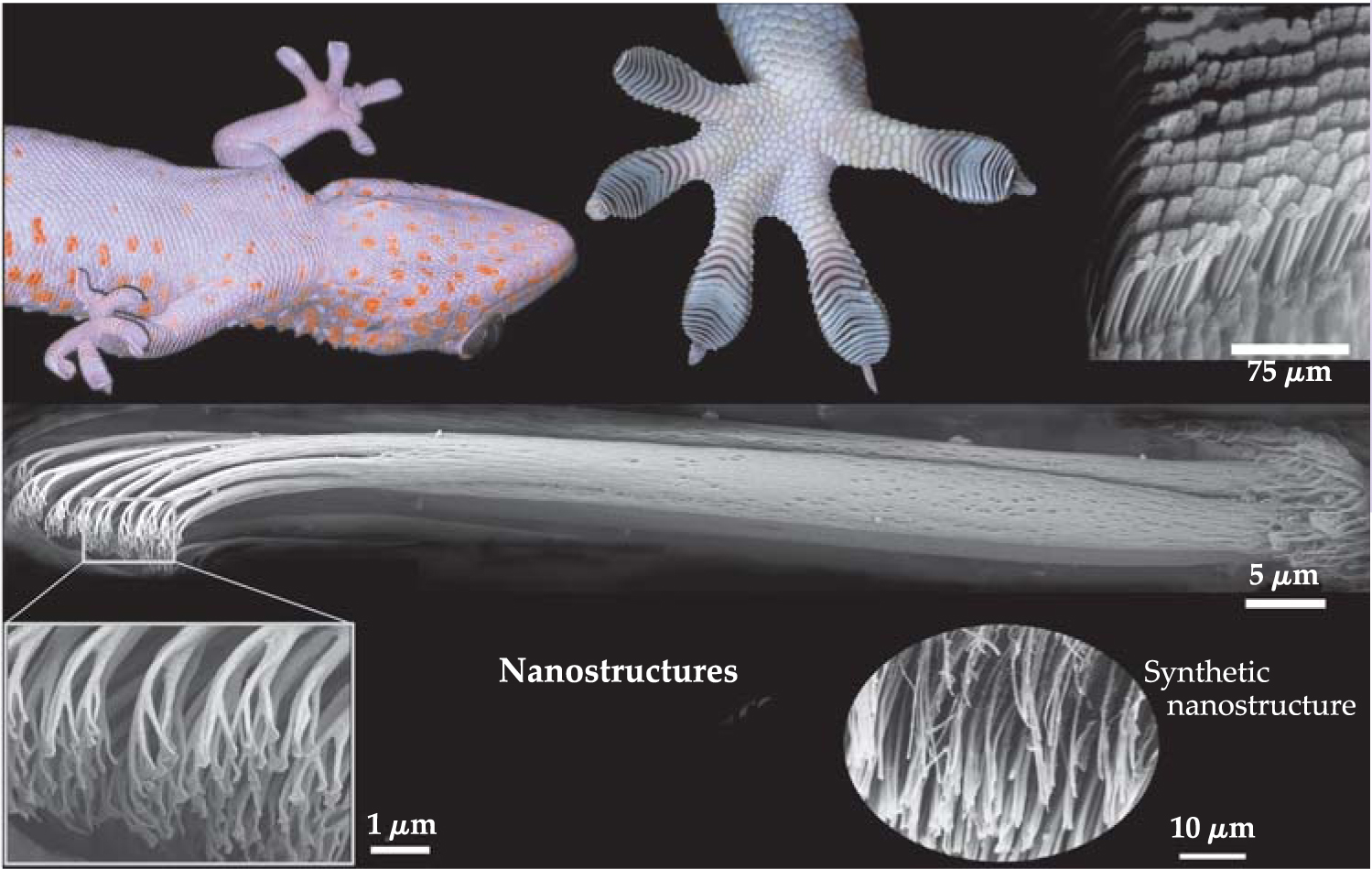
Another of nature’s spectacles—the amazing ability of the gecko to walk, or even run, across ceilings without the means of a sticky substance or mechanical device such as a claw—can be explained in terms of van der Waals forces. Kellar Autumn and coworkers at Lewis and Clark College have conclusively proven that the sticking powers of the gecko’s toes are due to the molecular attractive forces between closely spaced surfaces. 17 As shown in figure 6, the structure of the gecko foot is quite complicated. At the nanoscale, individual setae terminate in a small pad. The attractive force between the pad of a freshly plucked setal array (the gecko doesn’t seem to mind too much) and various surfaces has been directly measured to be in good agreement with expected molecular attractive forces. In fact, the special structure of the gecko’s foot makes it self-cleaning and has inspired the development of a new type of adhesive tape.

Figure 6. A gecko foot is depicted at various length scales. Visible at the smallest scale are the setal pads responsible for the van der Waals sticking that allows a gecko to walk on ceilings. The oval in the lower right shows a synthetic nanostructure inspired by the setal pads.
(Courtesy of Kellar Autumn, Lewis and Clark College.)
Changing times
Casimir, in his quest to understand the simplicity of the result he obtained with Polder, came to the startling conclusion that the zero-point energy of the electromagnetic field leads to the attraction between nonpolar molecules or atoms. Consequently, he extended his idea to derive the attractive force between two flat plates. The notion that the zero-point energy of the electromagnetic field could lead to observable consequences had been rejected by Pauli.
Times were changing, however. Julian Schwinger, Victor Weisskopf, and J. Robert Oppenheimer recognized that the Lamb shift could be understood as the interaction of a hydrogen atom with the zero-point fluctuations of the electromagnetic field. That recognition provided the basis for Hans Bethe’s 1947 calculation of the Lamb shift (see the article by Freeman Dyson, Physics Today, October 2005, page 48
References
1. H. B. G. Casimir, D. Polder, Phys. Rev. 73, 360 (1948).
2. H. B. G. Casimir, J. Chim. Phys 46, 407 (1949).
3. H. B. G. Casimir, Proc. K. Ned. Akad. Wet. 51, 793 (1948).
4. E. M. Lifshitz, J. Exp. Theor. Phys. 2, 73 (1956).
5. S. H. B. G. Casimir, Comments Mod. Phys. 5–6, 175 (2000).
6. See B. V. Derjaguin, Sci. Am., July 1960, p. 47. https://doi.org/10.1038/scientificamerican0760-47
7. B. M. Axilrod, E. Teller, J. Chem. Phys. 11, 299 (1943).
8. P. W. Milonni, The Quantum Vacuum: An Introduction to Quantum Electrodynamics, Academic Press, San Diego, CA (1994).
9. W. Pauli, Pauli Lectures on Physics, Vol. 4: Statistical Mechanics, C. P. Enz, ed., MIT Press, Cambridge, MA (1973).
10. H. B. Callen, T. A. Welton, Phys. Rev. 83, 34 (1951).
11. A. Lambrecht, S. Reynaud, Phys. Rev. Lett. 84, 5672 (2000);
S. K. Lamoreaux, Phys. Rev. Lett. 84, 5673 (2000).12. M. Boström, B. E. Sernelius, Phys. Rev. Lett. 84, 4757 (2000).
13. Special issue,“Focus on Casimir Forces,” New J. Phys. 8 (October 2006).
14. M. Elbaum, M. Schick, Phys. Rev. Lett. 66, 1713 (1991).
15. M. Elbaum, S. G. Lipson, J. G. Dash, J. Cryst. Growth 129, 491 (1993).
16. J. G. Dash, J. S. Wettlaufer, Can. J. Phys. 81, 201 (2003).
17. K. Autumn et al., Proc. Natl. Acad. Sci. USA 99, 12252 (2002);
K. Autumn, Am. Sci. 94, 124 (2006).
More about the Authors
Steve Lamoreaux (steve.lamoreaux@yale.edu
Steve K. Lamoreaux. steve.lamoreaux@yale.edu, Yale University, New Haven, Connecticut, US..




