A tangled tale of topological fluids

We physicists love simple problems. So much so that our immediate reaction to complex puzzles is to keep staring at them until some simple picture suggests itself. Sometimes we invent mathematical versions of those pictures: For example, a mean-field theory of atomic magnetism replaces a lattice of millions of atomic spins with just one spin interacting with a field that accounts for the mean effect of all the others. The best simple ideas also carry with them another notion—universality. Phase transitions in magnets share the same essential structures with the apparently remote behavior of fluids at their critical points. Universality arises when the essential physics emerges at large length scales. It also guides theorists who “renormalize” the complex fine detail of a system into an emergent structure that has just a few parameters. A classic example is the mean-field theory of entangled polymer dynamics, one of the products of the beautiful and still-youthful field of soft-matter physics. The story begins half a century ago but continues to present researchers with intriguing problems.

Macromolecules, giant strings of thousands of small molecular units, often display universal behavior. Many of the physical properties of polymers arise purely from the connectivity of their molecular chains rather than from the chemistry of their monomer units. As a result, for example, the spatial correlations of concentration in fluids of linear polymers have a long-range Coulomb-like decay. The phenomenon of rubber elasticity, to take another example, is analogous to ideal-gas pressure. In a gas the tendency toward greater translational entropy is responsible for the outward springiness of a pumped-up bicycle tire. In rubber it’s the lure of more random, crumpled configurations of the polymer chains that leads to the equally springy retraction of a stretched elastic band. Rubber’s elasticity is not governed by its detailed chemistry; rather, it is controlled by the density of the cross-links that anchor the ends of the thermally writhing polymer chains.

In the field of polymer rheology (the physics of flow and deformation of materials), more is at stake than figuring out a set of fascinating universal phenomena. Those who produce the billions of tons of plastic materials manufactured globally each year depend on getting right both the molecular constitution and the processing of polymers in their fluid phases. Even commonplace products, such as polyethylene sheeting, are manufactured in processes full of the delicate interplay of elastic stresses, beautiful fluid dynamics, and phase changes. Figure 1 shows one such process, the blowing of a polymer film. It is empirically essential to create the right blend of molecules—small and large, linear and branched—to stabilize the flow, thin the film uniformly, and endow the finished product with the right mechanical properties.

For two generations new materials have been developed essentially by trial and error: By varying the conditions of the chemical polymerization, polymer producers arrive at a range of good and bad materials. How much better it would be if the rules that connected molecular structure to flow properties were known. Then, in the words of BASF’s Erik Wassner, one could “reverse the design arrow” in the plastics industry and design new materials at the molecular level, much as is beginning to happen with pharmaceuticals. Such a capability is all the more desirable as new catalysts are developed that will allow much greater control of polymerization at the industrial scale. With its mix of fascinating physics and applications, polymer dynamics is one of those deeply satisfying fields of physics that bring university and industry teams together in a natural way.

Three physics themes

The quest for the fundamental rules of densely entangled polymer dynamics is assisted greatly by the emergence of universality. As noted above, for example, rubber’s elasticity is governed by cross-link density, not detailed chemistry. Now if the cross-links are taken away, one might imagine that all elasticity would vanish and yield a fluid, albeit a rather viscous one. But when the chains are strongly overlapped, as in a polymer melt, something wonderful happens instead; you may have experienced it if you’ve pulled hot pizza cheese or, more industrially relevant, worked with a melted plastic flowing during its process route. A stretching or shearing strain on the polymeric fluid produces an elastic stress just as it does when cross-links tie the molecular chains to each other. The difference is that the stress slowly dies away (the pizza cheese strings slowly start to stretch), following a decay curve that seems to reflect the structure of the macromolecules. At long times the material is indeed a fluid characterized by its viscosity η. But at shorter times the elastic response dominates, almost as if some cross-links were still there in fleeting form. That is the phenomenon of viscoelasticity.

The longer the chains, or the higher their molecular weight M, the slower the decay; astonishingly, molecular correlation times can extend to many seconds. Experimenting with different chemistries revealed a universal aspect to that relation, known as the 3.4 law: η ∝ M ^3,4 . More beautiful chemistry unearthed further surprises. It is possible to couple polymer chains in a controlled way to produce macromolecules with complex topology, such as star polymers with three, four, or even many tens of polymeric arms. Melts of such star polymers may be compared with those of linear chains to see how stress relaxes at fixed strain; for the comparison to be fair, the mean length of the linear chains should be comparable to the diameter of the stars. The difference is so startling that for years it was assumed that the star polymers cross-linked in some way, for the viscosity of the star polymers can be many orders of magnitude larger than that of the linear chains. Changing the topology of a polymer melt of high molecular weight by adding a branch at the spectroscopically undetectable level of one carbon atom in 100 000 was enough to increase relaxation times by 10 000 or more.

More intriguing phenomena emerged in the nonlinear response to large strains or large strain rates. A long tradition of nonlinear rheology had been motivated by engineering, since all polymer-melt processing—manufacture of thin films or fibers, for example—requires very large strain in the course of the polymer’s deformation history. As the shear-strain rate on a polymer melt increases, so initially does the stress—the proportionality constant is just the viscosity. But soon the linear relationship breaks down. At high shear rates, the stress is lower than the extrapolation of simple viscous behavior would indicate. However, the dominant geometry of deformation in process flows is not shear but extension; one or more dimensions of the material grow while others shrink. Perhaps the corresponding extensional stresses also “soften” at higher rates? The answer to the question serves as another universal differentiator of molecular topology. Of the two common industrial forms of polyethylene, for example, one (high density, or HDPE) contains predominantly linear molecules, and the other (low density, or LDPE) highly branched forms. Linear HDPE behaves similarly in shear and extension. But LDPE develops opposite responses in the two geometries, softening in shear yet hardening in extension.

Universality, topology, emergence—a strong collection of physics themes together with significant experimental results demand some conceptual framework. The only candidates as of about 1970 were modifications of theories for dilute chains by Prince Rouse and Bruno Zimm, but none of those came even qualitatively close to the phenomenology of the melt state. The missing ingredient was some characteristic length scale corresponding to a level of temporary elasticity. The breakthrough came via a recognition of emergent mean-field simplicity and an idea whose components came from two great theoreticians, Sam Edwards in the UK and Pierre-Gilles de Gennes of France.

Wriggling in a tube

In 1967 Edwards was tackling a problem in the elasticity of cross-linked polymer networks. The measured modulus was rather higher than predicted by the simple theory. He realized that the naive calculations were wrongly assuming the chains themselves could pass right through each other. Instead, Edwards postulated that the presence of neighboring chains would effectively create a tube constraining any given chain. The model required just one parameter, the tube diameter a. Interestingly, the value needed for a was large enough to require a truly polymeric section of chain to traverse it, and that meant the local molecular detail would have a weak effect on the nature of the tube—a route into universality.

Inspired by Edwards’s idea, in 1971 de Gennes took a step from equilibrium to dynamics. Suppose a chain that is not cross-linked were free to diffuse in a polymer network. Would its random motion not also be limited by the tube-like constraints? If so, only the chain ends would be able to choose random directions for thermal displacements; all other pieces of chain would have to diffuse into sections of tube just vacated by others. De Gennes coined the term “reptation” for the snake-like dynamics of an entangled chain. Crucially, he also derived the emergence of a critical disengagement time τ_d for a chain to diffuse out of its constraining tube, as illustrated in figure 2(a), into a neighboring tube. Simple scaling analysis gave τ_d ∝ M ³.

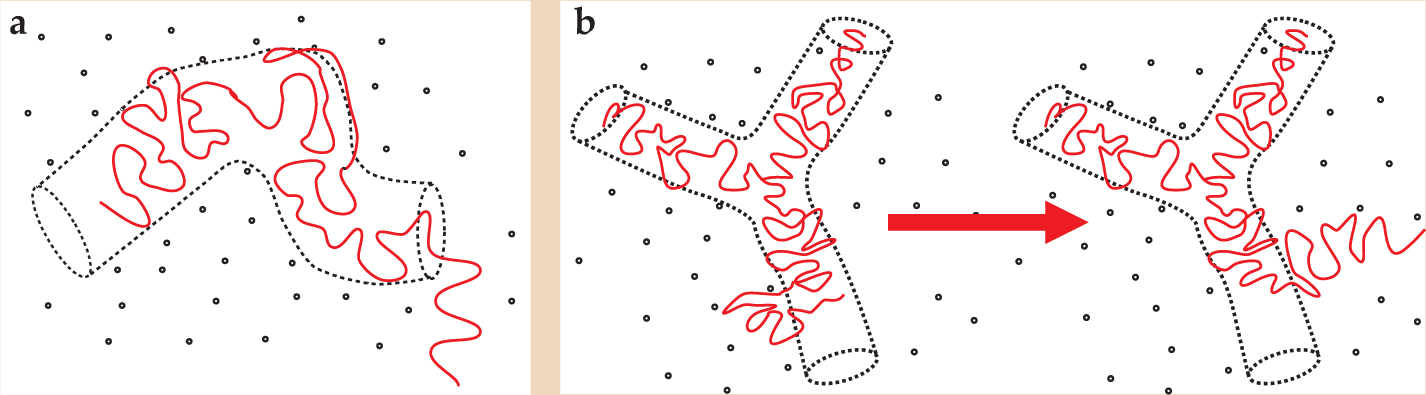
De Gennes’s result is, of course, suggestively close to the 3.4-law experimental scaling of polymer-melt viscosity with molecular weight. What was more remarkable, the consequences of a tube theory for a chain free at one end but linked to the network at the other were clear. The chain cannot reconfigure by reptation but only by deep retractions of the free arm along the entire length of its tube—a process exponentially slow in the molecular weight of the arm. But in 1972 the connection with melts of linear polymers in the first case and star polymers in the second (figure 2(b)) was made neither by de Gennes nor anyone else. After all, how could a tube of constraints survive for the lifetime of the chain they contain, when those constraints themselves would typically disappear on the same time scale? The argument that the turning on and off of constraining tubes would actually be a secondary effect rather than a primary one was due to Masao Doi, a visiting scholar from the University of Tokyo to Edwards’s Cambridge University group in the late 1970s. Doi and Edwards crafted the idea of reptation into a first theory of viscoelasticity. Interestingly, it was not the agreement, qualitative at best, of the linear response that attracted the attention of the rheological community but the fact that the theory gave correct predictions—sometimes with no free parameters—for a nonlinear response.

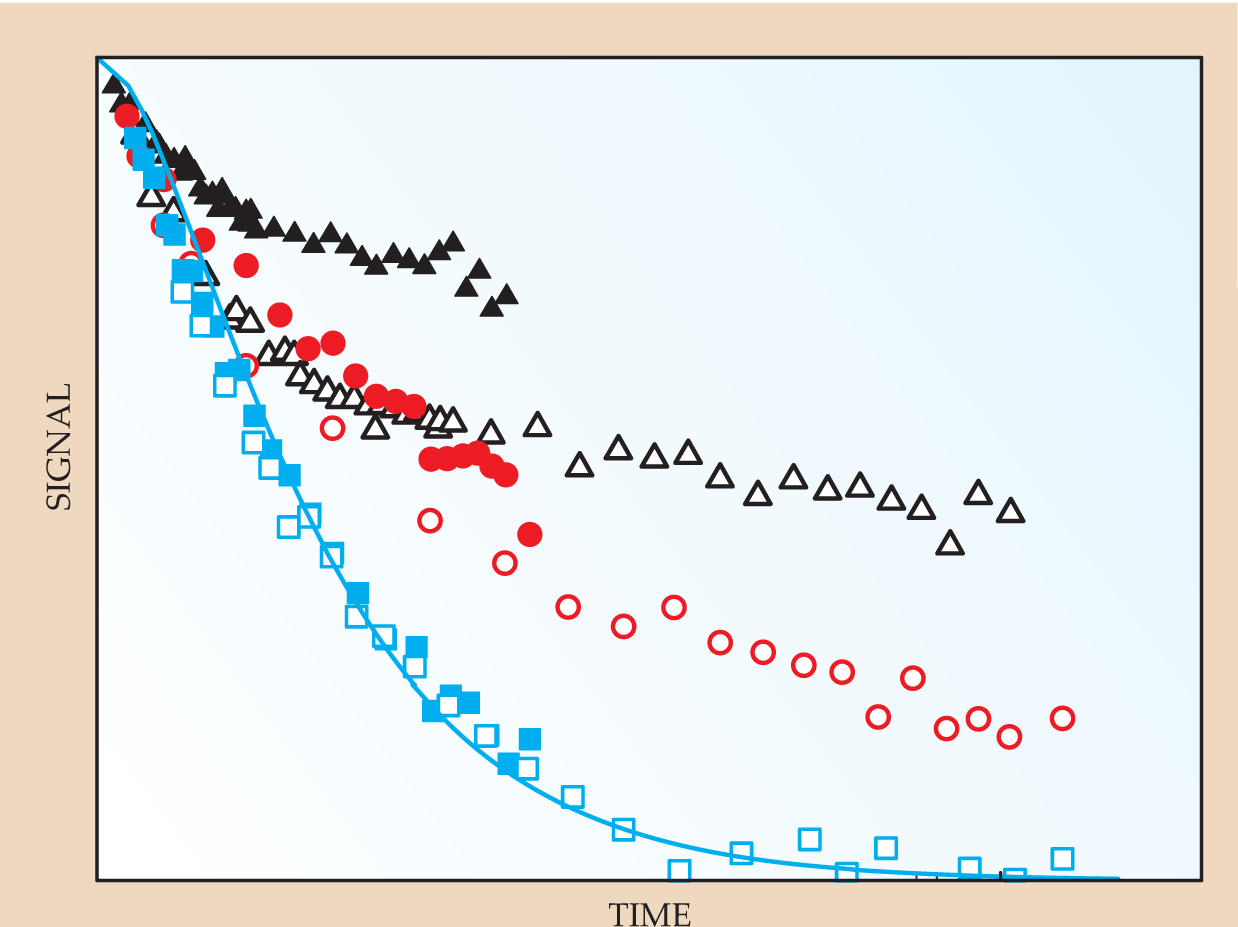
Suddenly the field of molecular polymer rheology was opened up, and the next 20 years saw a creative flowering of experimental techniques newly applied to entangled polymer systems, developments of the theory, and a serendipitous harnessing of the increasing power of simulation. The community was quick to realize that a microscopic theory of rheology had much more to say about a fluid than simply how stress and strain were related: Aspects of the polymer conformation and dynamics themselves were also testable. Arguably, the first technique to “see” the tube constraints was the neutron spin-echo scattering technique, applied first to a deuterium-labeled melt by Julia Higgins of Imperial College London and further developed by Dieter Richter and colleagues at Research Center Jülich. The spatial and temporal range of NSE is ideal for the study of entangled polymers. For such polymers as polyethylene, which is made from fast-moving and light monomers, the technique allows one to see early-time behavior dominated by local pieces of essentially free chain, then slower motion as the chains begin to feel the tube constraints (see figure 3).

Other experiments, which combined rheology with optical methods on partially labeled chains, began to identify which parts of entangled chains were responsible for stress relaxation at different time scales. If, after a sample chain is deformed, a chemically labeled section is optically followed, then the contribution of the labeled section can be compared with the overall relaxation. In that way the groups of Gerald Fuller at Stanford University and Lucien Monnerie at the École Supérieure de Physique et de Chimie Industrielles were able to detect much faster stress relaxation near the ends of chains than toward their centers. Those end bits are just the segments that require smaller diffusion distances to explore new tube constraints.

Star power

The largest differences between spatially resolved relaxations were seen by the École Supérieure group in carefully labeled star polymers. Trapped in a nexus of many converging tubes, the star-polymer branch point cannot diffuse but, as de Gennes saw for dangling arms in a network, must explore new configurations by deep, thermally activated retractions and reextensions into the surrounding melt, as shown in figure 2(b). Working with synthetic chemist Lewis Fetters at Exxon Research and Engineering Co and Eugene Helfand at Bell Telephone Laboratories, the late Dale Pearson (also at Exxon Research) brought both theory and experiment to bear on a remarkable conclusion: Since star-polymer arms relax stress independently of the diffusion of the I whole molecule, the viscosity of a star melt is independent of the number of arms but exponentially dependent on the arm’s molecular weight. All looked at first to be in perfect agreement with experiment, but it turned out that in the star melts lurked a puzzle that would help unlock a vital unresolved piece of the physics. To fit Fetters’s data on star relaxation, Pearson and Helfand had had to adjust the value of an order-unity constant v in the formula for the relaxation time τ_arm of an entire entangled arm of molecular weight M _arm. The exponential relation τ_arm ∝ exp(vM _arm/M _e) includes a measurable “entanglement molecular weight” M _e. The theory had no room for v as a free parameter, predicting its value to be 3/2. But the star data only worked with v = 1/2. The factor of three might seem a small price to pay, but v is multiplied by a large number and exponentiated. The theory actually overpredicted the viscosity of star polymers by a factor of many millions—a problem amusingly unnoticed for a few years.

The star polymers were shining a spotlight onto an old problem: What is the real nature of constraint release? In other words, how should one handle a tube of temporary topological constraints that winks into and out of existence at the same rate as a chain escaping from the tube itself? Clearly, the star-polymer data demanded a self-consistent theory. In the case of well-entangled star melts, the exponentially large range of time scales—from fast retractions near the chain ends to very slow, deep reconfigurations of entire arms—leads to a great simplification: Any relaxing segment interacts only with some far faster ones, which cannot entangle it, and some far slower ones, which always do. The effective constraining tube can arise only from the population of slow constraints, so it must be larger in diameter than the tube for linear polymers of the same chemistry. Robin Ball (University of Warwick) and I considered that dynamic tube dilation idea and constructed a mathematical formulation that with later refinements with Scott Milner of Exxon Research (now at the Pennsylvania State University) was widely used to model data from polystyrenes, polybutadienes, and more. Almost as a byproduct of thinking about stars, we came to understand why linear polymers are governed by an apparent 3.4 law rather than an “exactly 3” law: The same types of fluctuations that are the only means of entanglement escape for star polymers are certainly present in linear chains as well.

What of constraint release in linear polymers? In that case another beautifully simple picture emerges. The tube mimics many of the properties of a polymer, including its dynamics. If an entanglement is rearranged locally, then the tube just suffers a local “hop” in its configuration. Because the tube itself is not constrained, its hop is exactly analogous to a diffusive hop of a monomer in an unentangled polymer—for which the Rouse model had for decades been the known solution. The current picture of entangled linear chains therefore combines two idealized forms of polymer dynamics: the reptating and fluctuating chain in a fixed tube and Rouse-like unentangled dynamics for the tube itself. The existence of the tube was confirmed in 1990 with a protean effort and application of then-vast computational resources by Gary Grest (Sandia National Laboratories) and Kurt Kremer (Max Planck Institute for Polymer Research). Their many-chain simulations produced tube-like regions of constraint around every test chain; those survived while the chains diffused along the tube lengths.

Constraint release came to the rescue once more as the theory addressed continuous flows. The original Doi–Edwards pure reptation formulation predicted that for a steady shear flow, the stress would go through a maximum as a function of shear-strain rate, simply because chains tend to align with the flow. A fluid possessing a branch of its stress response curve with negative slope must give rise to instabilities in shear flow. Such unstable flow has been measured in certain surfactant fluids, in which entangled chains of self-assembled worm-like micelles undergo continual breaking and reformation as well as reptation. Michael Cates, then at Cambridge University, showed in 1987 that such coupled dynamics narrows the distribution of stress relaxation times and, later, that one consequence is a regime of unstable flow that breaks up into shear bands where fluid regions of different viscosity coexist. More recently Peter Olmsted and Suzanne Fielding at the University of Leeds showed that a rich nonlinear dynamical system arises from such banding instabilities, some of which had already appeared in beautiful flow-visualization nuclear magnetic resonance experiments by Paul Callaghan’s group at Victoria University of Wellington.

Physicists are currently debating whether banding instabilities arise in the case of linear polymers, partly because the actual response of those polymers at high shear-strain rates can show a near plateau rather than a maximum. Recent experiments by Shi-Qing Wang (University of Akron) and Thomas Hu (Unilever) have demonstrated a rich family of inhomogeneous flow behavior in entangled solutions, including the apparent formation of slip planes and transient shear bands. Those experiments and their theoretical interpretation are being hotly debated.

Whatever the extent to which entangled linear melts may thin in high shear, it is certainly not to the violent degree predicted by the tube model with reptation alone. The elegant solution came from Giuseppe Marrucci and colleagues at the University of Naples, who realized that another mechanism contributes to control release once flow rates overcome reptation. Neighboring chains are convected past each other by the flow and by diffusion, and the constraint-release rate becomes geared to the flow rate itself. At the structural level, such “convective constraint release” constantly injects new kinks into the chains in the sheared melt. So the polymers are never combed entirely flat by the flow and the stress remains monotonic with shear-strain rate.

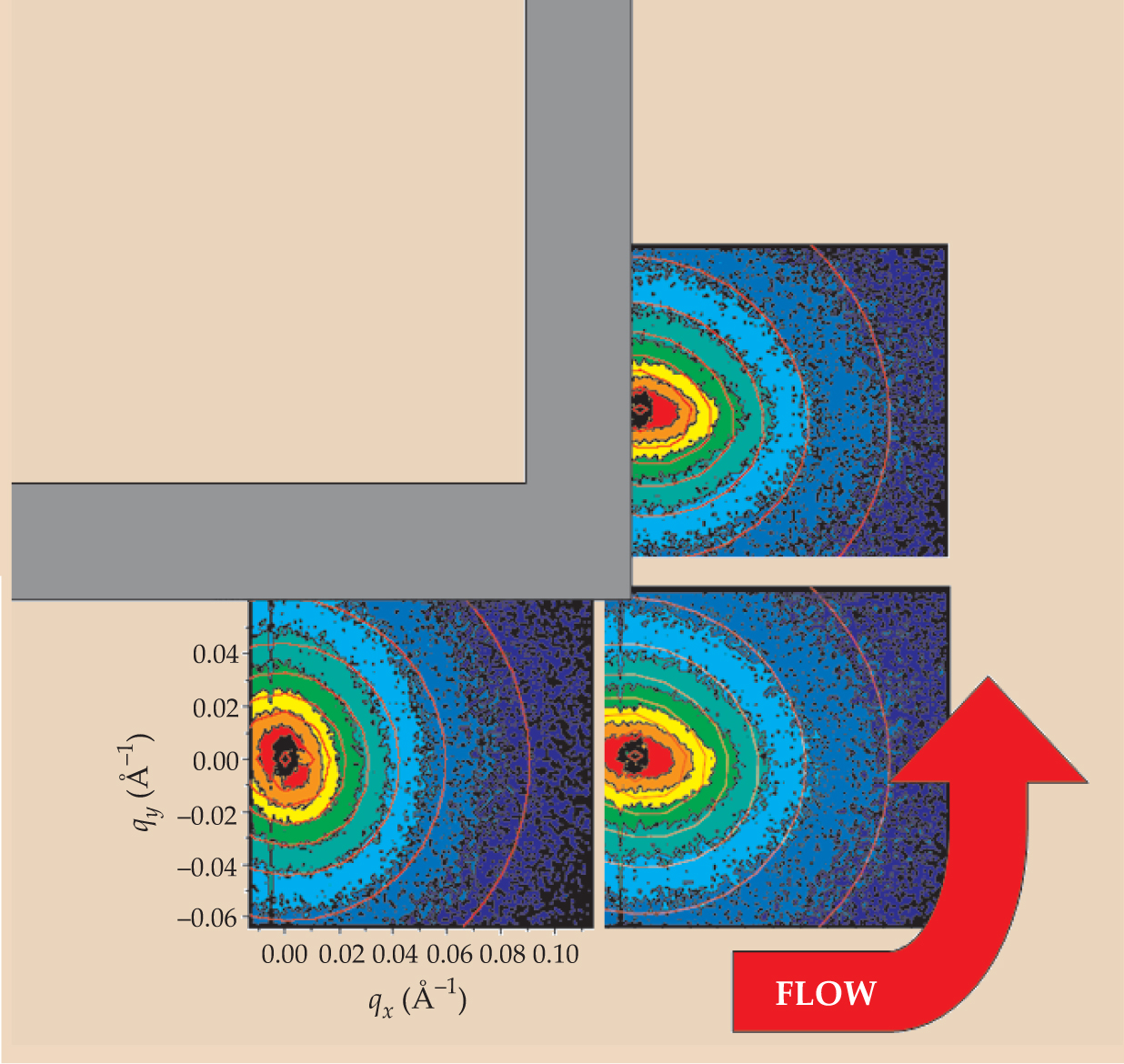
A broad UK-based collaboration recently developed the technique of neutron flow-mapping, in which the chain configurations in a flowing melt are scanned by neutron diffraction. That development represents a key step to connecting microscopic dynamics of linear polymer melts all the way through to their process flows. Figure 4 shows measured chain diffraction patterns for a melt flowing around a sharp corner, compared with the predictions of a state-of-the-art tube theory. Ultimately such work could allow manufacturers to place polymer chains in their optimal orientations for product properties.

More general forms

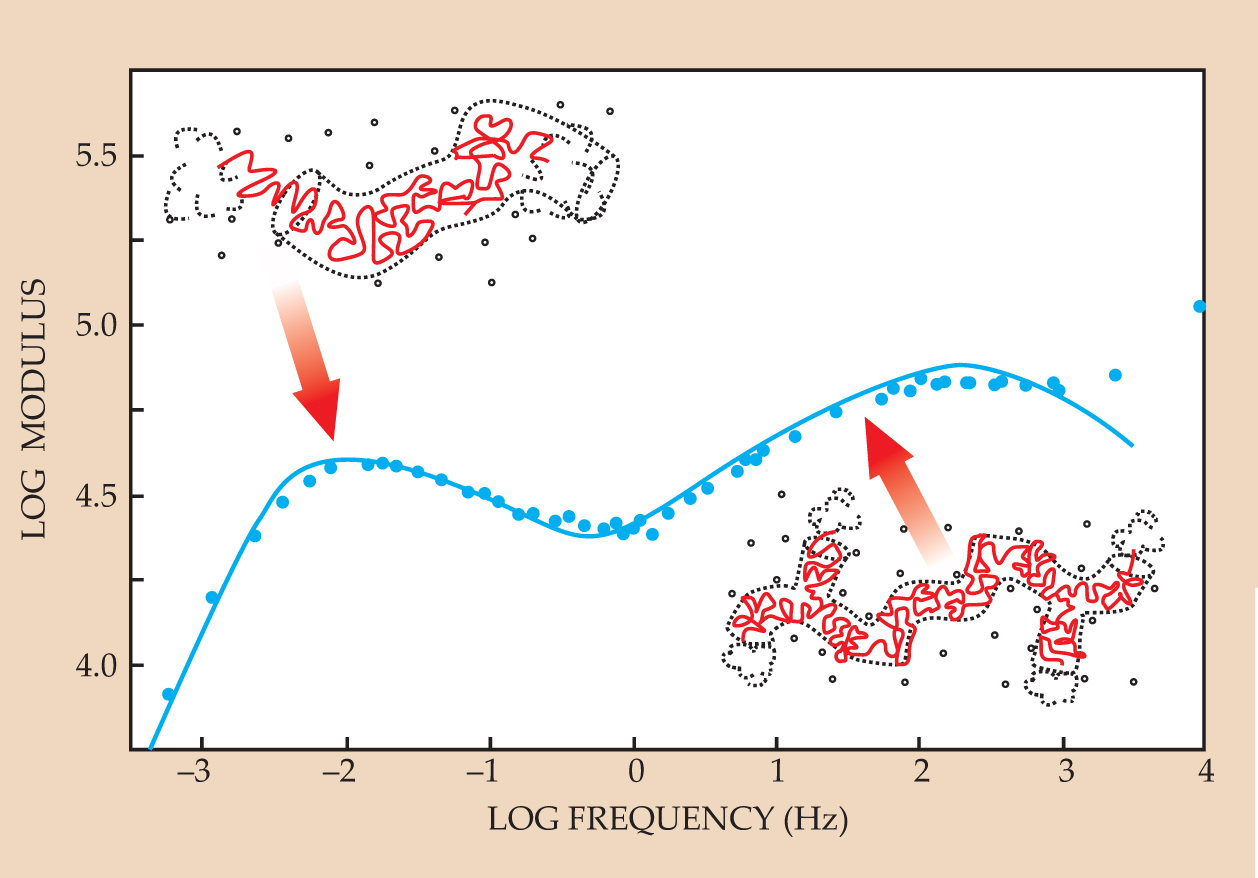
Dilating stars forced physicists to address more carefully the temporary nature of constraining tubes, but the story of branched polymers doesn’t end there. In the 1980s, more imaginative architectures already were being created. Jacques Roovers, then at the University of Waterloo, had made a series of polystyrene “H-polymers,” for example, in which each molecule contained two branch points separated by a cross-bar section. I was fascinated by the complex rheological spectra that Roovers had measured from those wonderful materials and became convinced that the tube model had in itself the capability to predict the relaxation dynamics for any architecture. If so, then the H-polymer looked like the next step. The theoretical recipe was becoming clearer: Take your molecule, dress it up in a self-consistent tube, and allow fluctuations that retract the arms to reconfigure the tube. Doing so for the H-polymer gave a star-arm-like relaxation for the arms and then, at much longer time scales, a diluted reptation dynamics for the cross bar. Experiments with synthetic H-melts of more highly entangled polyisoprene by a team of which I was a part confirmed that picture and opened the door to still more complex architectures. Figure 5 shows some of our data.

Ronald Larson (University of Michigan) had had a long-standing interest in the highly branched industrial material LDPE. As a chemical engineer with a strong interest in molecular physics, he was puzzled that the strange nonlinear response of LDPE was not captured even qualitatively by any phenomenological model. He and I suspected that if the tube physics for more highly branched molecules such as the H-polymer were pushed to the nonlinear regime, it might provide a clue. The hunch proved correct. Our analysis of the more general “pom-pom” molecule, in which the two branch points carry arbitrary numbers of arms, showed that the key ingredient was the existence of two relaxation times of any entangled segment of a branched polymer. The slower time controls the molecule’s linear response and is set by the diffusive entanglement escape—that is, arm relaxation and reptation. The faster relaxation time appears only in nonlinear flows and is set by the retraction of chain stretch analogous to a rubber band snapping. A mathematical toolkit built out of pom-pom modes turns out to be able to encompass quantitatively the rheology of any industrial LDPE.

Nonetheless, a problem remained with calculating the dynamics of complex branch-on-branch architectures. When a dangling arm relaxes back to its branch point, deeper sections of the molecule can be mobilized. But by how much are they mobilized, and with what effective drag? Recently those questions were addressed by Daniel Read and Chin-may Das at the University of Leeds, who realized that the relaxation of highly branched polymers is controlled by two “relaxation fronts” that move from the extremities to the core. One traces the disentanglement wave itself, but it is preceded by a “mobility front” that signals the effective branching point for all the active retraction modes that are currently releasing entanglements. Their enhanced theory re-created the experimental relaxation spectra of an entire series of test polyethylenes. If that essentially complete theory of the linear response of arbitrary architectures can be extended to the nonlinear response—no mean feat—then the exciting prospect of in silico design of polymer materials comes a lot nearer.

While some soft-matter physicists have been pushing on the outer frontier of complexity and application, others have exemplified the renewed interest at the inner frontier of fundamentals. Where and how do chain-chain topological interactions arise? What microscopic features of the polymers themselves set the parameters of the tube model? Ralf Everaers (University of Mainz), Kremer, and others have explored those questions numerically by an ingenious application of an early thought experiment. Doi and Edwards had imagined that winding through the melt was an irreducible “primitive path” that defined the tube geometry for a test chain; it was obtained by a process of “reeling up” the chain length in all the molecules of an entangled volume. That is, all chains shorten until they become tense and cannot reduce further in length because they are entangled with other chains. Statistics of the path length can be explored, as can the critical chain–chain interactions that determine them, since entanglements can be associated with kinks in the primitive paths. The scaling of primitive-path length—or, equivalently, entanglement density—with polymer concentration does not follow the same scaling rule as melts seem to show. The reason may lie in many-body topological interactions that more subtle primitive-path analyses will uncover.

Ringing changes

New ideas on the origin of the tube are being stimulated by the one polymer architecture that still eludes a quantitative model of any kind: the ring. A moment’s reflection indicates that ring molecules must behave in an idiosyncratic way, since all other entangled dynamics, whether reptation of linear polymers or fluctuation of branched ones, are driven by the free ends. Ring polymers just don’t have them. Early statistical mechanics calculations by Cates (now at the University of Edinburgh) and Joshua Deutsch (University of California, Santa Cruz) suggested that even the static configurations of rings would be more compact than random chains in the melt. Later work by Sergei Obukhov (University of Florida), Michael Rubinstein (Eastman Kodak Co), and Thomas Duke (Princeton University) proposed that ring polymers would self-organize into multiply branched objects that changed configuration by amoeba-like extension and retraction of doubly looped limbs, as shown in figure 6.

The experiments were even stranger. Some claimed that ring melts were more viscous than their linear counterparts of equal molecular weight, others claimed the opposite. Dimitris Vlassopoulos and his group at IESL-FORTH in Crete seem to have found the culprit in low levels of linear contaminants. For some reason even tiny amounts of linear material threading a ring melt can greatly extend relaxation times beyond those of either pure component. When rings are made as pure as possible, the relaxation spectrum indeed follows that predicted by the self-similar dynamics of Obukhov, Rubinstein, and Duke. That’s actually somewhat surprising because the predictions were made for a ring in a fixed network, not in a melt, and they took no account of constraint release. Since constraint release is so important in all other architectures, it is hard to see how it could somehow switch off in rings.

The problematic case of ring melts has been at the back of my mind since I had a very pleasant encounter with two solar physicists a few years ago. They were busily doing calculations in a model I recognized as an extension of Rouse polymer dynamics—but their calculations were for bundles of magnetic flux in the Sun. It is still unclear to what extent the effective polymer physics of the solar magnetic fields contributes to the plasma viscosity, but the absence of magnetic monopoles means that if relevant at all, the polymer architecture is that of rings.

The field of entangled polymer dynamics now stands at a crucial and exciting point. On the one hand, the fundamental emergent processes in the standard case of flexible, noninteracting chains seem to have been established. The challenge is to fulfill the promise to “reverse the design arrow” in industrial materials science. Is it really possible to develop a methodology of quantitative molecular engineering in which the particular demands of a materials application are used to create new materials? If so, that would apply across the chemical spectrum from polyolefins to acrylics, or even to a new generation of polymeric materials that use non-oil-based sustainable chemistry. One of the “design features” industrial scientists must understand, if only to avoid it in practice, is the family of purely viscoelastic fluid instabilities that depend sensitively on the melt rheology The shear-banding subset is perhaps the most striking of those instabilities, but others generate oscillations, helical swirling, or chaotic flow inimical to successful processing—even if they are beautiful in their own right.

On the other hand, an understanding of the topological interactions constitutes a foundation for theories of more complex entangled macromolecules. The rheology of charged polymers, or polyelectrolytes, is still extremely mysterious and would be enough to fill a second article by itself. A different class of viscoelasticity emerges from polymers with strong local interactions that allow them to stick together for macroscopic time scales. Both charge and association contribute to tangled macromolecules in biology. A bacterium actually recruits special enzymes called topoisomerases to disentangle its own DNA, a fascinating example in the new field of active rheology. Other biological examples of entangled polymers can be found in the cytoskeletal components of actin, filamin, and microtubules. Those three materials are highly stiff macromolecules, whose flexibility appears only at length scales longer than the entanglement spacing. All subjects of current research, the novel macromolecules briefly introduced point to the familiar phenomenon in physics of every answer opening up a host of questions.