Transporting water to the tops of trees

Trees can rightly be called masters of microfluidics. In the stem of a large tree, the number of interconnected water transport conduits can exceed hundreds of millions, and their total length can be greater than several hundred kilometers. Furthermore, on a sunny day, a tree can transport hundreds of gallons of water from the soil to its leaves, and apparently do it effortlessly, without making a sound and without using any moving parts. On a global scale, the movement of water through plants makes a major contribution to the hydrologic cycle by providing the principal pathway through which water moves from the soil to the atmosphere.

The physics that underlies water transport through plants is not exotic; rather, the application of that physics in the microfluidic wood matrix results in transport regimes operating far outside our day-to-day experience. In this Quick Study, we seek to dispel some of the confusion surrounding how water is transported to the tops of trees and to highlight both the physical challenges and the structural solutions employed by those silent engineers.

Does physics limit tree height?

Plants require water in quantities that far exceed the demands of any animal. The reason for that thirst derives from the fact that the atmospheric concentration of carbon dioxide, the principal substrate for photosynthesis, is only about 0.038%. The scarcity of CO₂ means that mechanisms to concentrate it have limited efficacy, which forces plants to rely on diffusion to transport it from the atmosphere to the cells engaged in photosynthesis. The water cost of that reliance is high: For every CO₂ molecule that diffuses into a leaf, many water molecules diffuse out along what is often a much greater concentration gradient. Under the sunny and warm conditions that favor photosynthesis, the exchange ratio may be as unfavorable as 1 to 500. As a consequence, as much as 99% of the water that enters the roots travels upward through the stem to the leaves, where it evaporates and diffuses out through small pores in leaf surfaces.

What is the mechanism responsible for the large-scale movement of water? A plant whose roots have been cut off is able, at least for a while, to supply water to its leaves. That observation eliminates the possibility that some sort of pump operates in the roots and instead places the engine for water transport at the top of the plant. If asked to design such an engine, you might consider something like a vacuum pump, which drives mass flow by decreasing the pressure in the gas phase. However, the maximum height that one can lift water against gravity using that approach is 10.33 m. Trees that exceed 100 m in height, such as the coastal redwoods of California or the mountain ash of Australia, provide living proof that a fundamentally different mechanism is at play.

Plants supply water to their leaves using nothing more mysterious than capillary forces, albeit ingeniously deployed. Such forces are easy to observe in the lab. A glass tube supplied with water at its base lifts water against gravity as a result of the attraction of water molecules to the hydrophilic (wettable) glass surface, coupled with the large surface tension of the water (see the Quick Study by Laurent Courbin and Howard A. Stone, Physics Today, February 2007, page 84 ). The key element to note is that the pressure in the water is decreased due to the surface tension on the curved air–water interface; the pressure in the gas phase remains unchanged.

The relevant capillary dimensions are not those of the relatively large conduits that you would see if you cut down a tree and looked inside; their diameters are on the order of 50 to 100 µm. Rather, the appropriate dimensions are determined by the air–water interfaces in the cell walls of the leaves, where the matrix of cellulose microfibrils is highly wettable and the spacing between them results in effective pore diameters of something like 5 to 10 nm. A wettable capillary with a diameter of 2.91 µm pulls on water just strongly enough to balance the 0.1 MPa atmospheric pressure, so the pressure in the water is zero. For smaller diameters, the capillary force is capable of lifting water higher than 10.33 m. For example, the maximum height of a water column with a capillary diameter of 10 nm is nearly 3 km. Thus, one might ask not how trees can be so tall but instead why they are not taller.

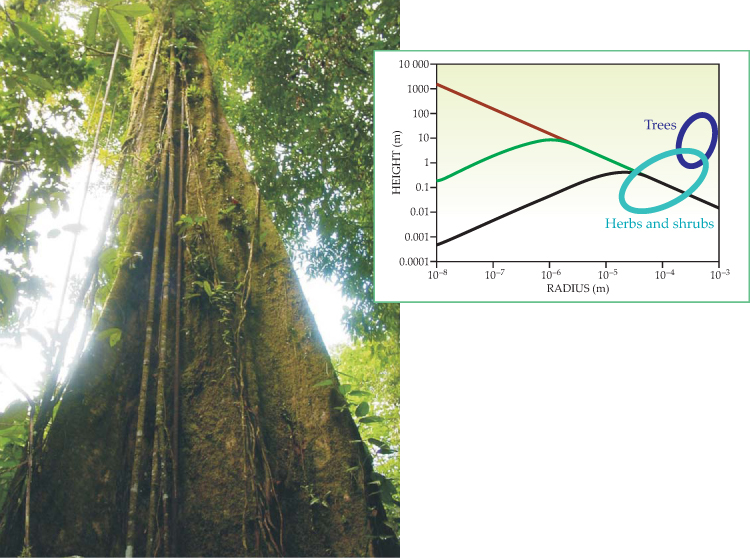
The answer, elaborated in the figure, involves the friction associated with the movement of water in the tree’s channels. Plants solve the problem of generating sufficient capillary forces while reducing viscous losses by connecting the small capillaries in the leaves to larger ones that provide a much wider transport channel that runs from the veins in the leaf down through the stem and into the roots. The transport channel allows for a continuous liquid path that extends into the soil. However, increasing the diameter of the conduits creates a new problem—that of transporting water under tension.

Life in a metastable state

The forces required to move water to the tops of trees are large. Gravity imposes a pressure gradient of 0.01 MPa/m. In addition, trees must work both to overcome friction and to pull water from the soil. The magnitude of the capillary forces that pull upward on the water column depends on how dry the soil is, how quickly water evaporates from leaves, how tall the tree is, and the number and dimensions of the microcapillaries through which the water must flow. When the magnitude of the pressure due to the capillary force exceeds atmospheric pressure, the net force on a bit of water in the capillary is outward; in other words, the pressure within the plant’s water column is less than zero.

Typical values at midday are about –1.5 to –2.5 MPa, although pressures as low as –12 MPa have been measured in arid regions. Negative pressures can occur in liquids if the intermolecular forces are sufficiently strong to keep the liquid molecules from pulling apart. In the case of water, extremely strong hydrogen bonds hold the molecules together.

But can negative pressure really work? What prevents the water column from transitioning to the vapor phase? As long as the pressure in the surrounding gas phase remains greater than that of the saturated vapor pressure, the water will not boil. The introduction of bubbles into the water column, however, represents a real danger to plants, although not because bubbles spontaneously nucleate—the strength of the hydrogen bonds renders that possibility very unlikely. Instead, a tree’s Achilles’ heel lies in the need to have water flow between conduits as it travels from the soil to the leaves. It is through the relatively porous regions of interconduit water movement that air can be pulled.

Whether an air bubble so introduced grows or shrinks depends on its size. If the bubble is sufficiently large, its inward-pulling surface tension will not be able to counteract the outward-pulling tensions exerted by the air–water menisci in the leaves; the bubble will expand. Because the transport conduits in trees are large compared with the pores where the tensile forces are generated, it is in the conduits where bubbles exceeding the critical radius for expansion can form. Furthermore, any increase in a bubble’s size reduces the force due to surface tension. So once a bubble starts to expand, it will continue to do so until it fills the entire conduit. Such a phase change would represent a serious, potentially permanent loss to the tree: The inability to transmit tensions through the gas phase means that a gas-filled or embolized conduit is useless for water transport. Because the presence of a bubble that exceeds the critical radius for expansion leads irreversibly to a change from the liquid to the vapor phase, water in the conduits is said to exist in a metastable state.

Trees use a variety of mechanisms to avoid the formation and spread of bubbles. The diversity of wood structures among the many species of trees reflects, in large part, different strategies for dealing with the dangers of transporting water under tension. In essence, trees may simply be solar-driven evaporative pumps that wick water up from the soil using capillary forces. But their ability to operate in a metastable state makes them unique among both natural and human-engineered transport systems.