Topological physics with light
DOI: 10.1063/PT.3.2394
Physicists classify and understand systems in terms of many properties; color, mass, and length are familiar examples. The theme of this Quick Study is a more subtle property—a system’s topology, or how its parts connect. As an example, a circular linked necklace can be deformed into an oval or a rectangle without changing the topology, since the links remain connected in the same way. But the necklace can only be made into the topologically distinct straight line if it is cut or its clasp is opened. In the 1980s physicists realized that some physical properties are entirely dictated by a system’s topology.
Skipping along the edge
The exemplar of a topological phenomenon is the quantum Hall effect (see Physics Today, December 1985, page 17
The quantum mechanical treatment of a free particle in the magnetic field, as first worked out by Lev Landau, yields a set of solutions that may be viewed as orbits that enclose a quantized amount of magnetic flux. Particles that are far away from the edges—in the bulk of the 2D material—can complete their orbits without running into the edges. Since such particles essentially stay in place, they do not contribute to conduction; rather, they make the material insulating.
But boundary conditions matter. When particles are near an edge, they can’t complete their orbits. Thus the particles skip along the edge, as shown in figure 1. The system, which is insulating in the bulk, becomes conducting because of its edge. Such a system is called a topological insulator.

Figure 1. Topological insulators. In the presence of a magnetic field B, charged particles in a topological insulator execute closed orbits inside the bulk but skip along the edge.

Remarkably, the conductance only depends on the presence of the edge, not on its particular shape; that puts the topology in topological insulator. Moreover, if one obstructs the edge with a disorder, the current routes around the obstacle. The conductance is robust, a remarkable and useful feature that enables quantum Hall systems to provide the standard realization of electrical resistance. On a more technical level, the robustness arises because the edges support a single direction of circulation, as one might expect for a particle in a magnetic field. Thus electron scattering by disorder is suppressed because the electron can’t reverse course, nor can it enter the insulating bulk.
Phase, not field, is the essence
Six years ago in a pioneering theoretical study, Duncan Haldane and Srinivas Raghu showed that such topological effects could be seen with photons. Their approach, however, relied on magneto-optical effects, which are extremely weak at optical frequencies. Thus the investigation of topological effects for photons was limited to the microwave domain. Since then, we, our collaborators, and others have developed alternative ways to realize topological physics with light.
At first blush, though, the very idea seems absurd: Photons are neutral and don’t respond to magnetic fields as a charged particle would. But we physicists have learned that the underlying physics behind topological effects is actually governed by the phase the electron wavefunction picks up when an electron goes around a loop. And such phases can be engineered for any particle, even neutral particles like photons. Moreover, no magnetic field is necessary.
Figure 2a represents the phase e−iϕ picked up by an orbiting electron as a “wiggle” for every 2π accumulated by the phase-factor ϕ. The two orbits in the figure each correspond to an integer number of wiggles, a necessary condition for a well-defined electron wavefunction. The accumulated phase corresponds to the action generated by translations of the total momentum (mechanical plus electromagnetic) along the path:

Here ℏ is Planck’s constant divided by 2π, p is the mechanical momentum of the particle, e is the magnitude of electron charge, and A is the vector potential whose curl is the magnetic field.
The term involving A in the above equation is proportional to the magnetic flux threading the orbit. Most importantly, if that contribution is positive for the clockwise path, it is negative for counterclockwise traversal. The two circulations lead to different numbers of wiggles, as shown in figure 2a, even for paths that enclose the same area. That’s the effect we want to replicate with light.

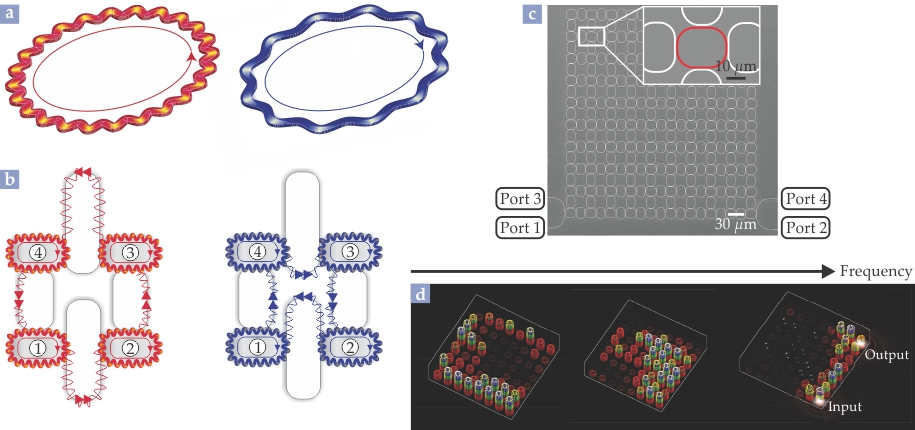
Figure 2. Topological physics with resonators. (a) A charged particle in a magnetic field satisfies a different quantization condition—the integer number of 2π phase wiggles in its wavefunction—when circulating counterclockwise (red) versus clockwise (blue). That difference is proportional to the magnetic flux threading the loop. (b) One can engineer a different number of wiggles for clockwise and counterclockwise circulation through an array of optical resonators. The illustration here shows a plaquette of four optical resonators coupled by waveguides. For the counterclockwise (red) path, light traveling from resonator 3 to resonator 4 travels a greater distance than light traveling along the clockwise (blue) path from 4 to 3. That length imbalance means that the phase picked up by photons is different for counterclockwise versus clockwise propagation. (c) Shown here is an electron micrograph of an array of optical resonators with waveguides, fabricated with silicon-on-insulator technology. Light enters and exits via waveguide ports on the bottom left and right of the device. In the inset the resonator is red and surrounding waveguides are white. (d) Depending on the frequency of light entering the array, light can take the long way around from input to output ports (left), be trapped in the bulk (center), or travel on just a single edge (right).
The phase of a photon wavefunction has a simple form; a photon with momentum p = ℏk traveling a distance r picks up a phase e−ikr. Evidently, if photons are to circulate around a structure and pick up different phases for clockwise and counterclockwise circulation, they must trace different paths for the two types of motion.
A simple implementation of that condition uses ring resonators, with photons circulating in a fixed way around their periphery. Figure 2b illustrates a plaquette of four such resonators; the photons circulate clockwise around each resonator. But, as the panel shows, a photon leaking out of one resonator and entering an adjacent one can be engineered to follow different paths depending on whether it goes left to right or right to left. Thus for motion around the four-resonator plaquette as a whole, the counterclockwise path is longer than the clockwise one; the photon picks up a greater number of phase wiggles for the counterclockwise trajectory.
In sum, a properly designed array of optical resonators (figure 2c shows an electron micrograph of our device) mimics a system in which charged particles hop from site to site in a magnetic field. To see that the photons are skipping along the edges of the resonator array, one can measure the transmission properties of the material or, as shown in figure 2d, directly image the light that leaks out of the device because of otherwise unwanted scattering.
Our approach to topological physics with light does not involve magnetic fields. Because of the absence of magnetic fields, which change sign when time is reversed, our system is analogous to other time-reversal invariant topological systems such as quantum spin Hall systems. (For more information, see the article by Xiao-Liang Qi and Shou-Cheng Zhang, Physics Today, January 2010, page 33
Where do we go from here?
Nowadays research efforts with light analogues of the topological insulator are focused on two different areas. One is the application of those devices to real-world challenges in photonic systems—for example, increasing the density of information that can be carried in optical fibers or creating robust on-chip delay lines. Disorder-resistant devices may well find wide-ranging applications.
The other principal focus involves adding interactions. So far, experimental efforts have been limited to noninteracting systems, as photons do not interact directly with each other. However, extremely rich physics arises when strong interactions are present. Of particular interest is the so-called fractional quantum Hall effect, which may even open the door to fault-tolerant quantum computation. (See Physics Today, December 1998, page 17
Adding interactions requires interfacing the photons with a material system such as an optical nonlinear medium, a Josephson junction, or more exotic nonlinear elements. Recent developments, including the first single-photon transistors and so-called photonic molecules, suggest that interacting photons are on their way.
References
1. F. Haldane, S. Raghu, “Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry,” Phys. Rev. Lett. 100, 013904 (2008). https://doi.org/10.1103/PhysRevLett.100.013904
2. Z. Wang et al., “Observation of unidirectional backscattering-immune topological electromagnetic states,” Nature 461, 772 (2009). https://doi.org/10.1038/nature08293
3. M. Hafezi et al., “Imaging topological edge states in silicon photonics,” Nat. Photonics 7, 1001 (2013). https://doi.org/10.1038/nphoton.2013.274
4. O. Firstenberg et al., “Attractive photons in a quantum nonlinear medium,” Nature 502, 71 (2013). https://doi.org/10.1038/nature12512
More about the authors
Mohammad Hafezi is a senior research associate at the Joint Quantum Institute of the University of Maryland in College Park. Jake Taylor is a staff physicist at NIST in Gaithersburg, Maryland, and a JQI Fellow.




