Quantum electrical Standards
DOI: 10.1063/1.3480089
Most people, including physicists , are probably not aware of how the voltmeter in a lab or the battery in a cell phone is calibrated. Both of those activities, and many others, depend crucially on the successful dissemination of electrical units based on the Système International. Standards for electrical units have a venerable history that dates back to fundamental experiments—for example, tests of Ampère’s law. Today’s electrical standards, though, are being challenged by modern work based on quantum laws and devices that did not exist when the SI was established in 1960.
In theory, electrical units are all based on the force between two current-carrying wires. In reality, the present system of electrical units is based on two inconvenient and challenging physics experiments. The unit of current is defined by a modern version of the Ampère experiment that uses a device called the watt balance (see figure 1). The unit of capacitance is defined by the calculable capacitor experiment, in which a large copper cylinder moves past other cylinders in a vacuum chamber. In actual practice, however, the calibration of most electrical units, in particular voltages and resistances, can be traced to solid-state devices that reflect quantum physics, not the classical Coulomb or Ampère laws.

Figure 1. The watt balance is used to realize the SI definition of current. When it is in operation, the mechanical power generated by a mass moving in Earth’s gravitational field is equal to the electrical power generated in a coil moving through a magnetic field.
(Courtesy of Rich Steiner.)

Quantum standards based on the Josephson voltage (JV) and quantum Hall resistance (QHR) are commonly used at national measurement laboratories such as NIST and at many high-tech companies. Although they do not realize SI units (that is, they don’t follow the SI definition), the quantum standards are much more convenient, reproducible, and easy to use than are the classical standards. Solid-state single-electron devices (SEDs) that move individual electrons about and allow those electrons to be counted offer the additional possibilities of fundamental current or capacitance standards based on the charge of the electron.
An unalloyed SI?
Since 1967 the SI definition of the second has been keyed to the frequency of a hyperfine transition in cesium-133. As the modern second illustrates, quantum standards are attractive because they are based on the values of fundamental constants through well-established simple laws of physics. By contrast, the kilogram is the only one of the seven base SI units that is not defined via a fundamental law of physics. It is instead based on “Le Grand K,” an artifact that is made of a platinum-iridium alloy and kept in a safe in international territory near Paris. The artifactual basis for the kilogram has profound implications not only for the mechanical units but also for the electrical units because the Ampère is defined in terms of the force between current-carrying wires.
The dichotomy between the excellent quantum standards for electrical units and the present-day realizations’ reliance on Le Grand K has inspired several groups to propose redefinitions of the electrical units. Here I will discuss one scheme, in which the values of Planck’s constant h and the electron charge e are defined exactly, with no uncertainty. Those two constants, and only those two, appear in two formulas, presumed to be exact: for the voltage V across a Josephson junction excited at frequency f, V = hf/2e, and for the resistance jump R predicted by the quantum Hall effect, R = h/2e 2. Thus, in the new scheme, the representations of voltage and resistance as commonly now disseminated from the JV and QHR standards would conform to the formal legal definitions of those units. In addition, the new quantum standards would allow the kilogram to be realized not through Le Grand K but rather via the watt balance. For that reason, the watt balance is also called the electronic kilogram.
A third possible standard involves SEDs that transfer electrons one by one. An individual armed with such a device can realize a current standard I = fe by clocking electrons through the device. Such a realization is attractive because the clocking frequencies can be determined with extraordinary accuracy.
The validity of the quantum formulas for the JV and QHR is crucial for the possible redefinition considered here for the SI electrical units. The standards for voltage, resistance, and current are connected by Ohm’s law V = IR, and checking the exactness and mutual consistency of the three standards through that fundamental principle is a sought-after goal in the metrology community. Confirming with an uncertainty of 0.1 part per million or better the consistency of the three formulas as linked through Ohm’s law would give added weight to the evidence supporting the redefinition.
How is it possible to fabricate devices that can move electrons around one at a time? Crucial to the operation of the SED is the result that the charging energy E to add a single electron to a capacitor with capacitance C is E = e 2/2C; with modern nanofabrication methods, C is so low that the energy is about 0.1-1 meV. By working at low temperatures and applying appropriate voltages to the SED, an experimenter can lower the energy barrier for a single electron to move from one capacitor to another from about e 2/2C to a much smaller value. Once the barrier is lowered, the electron is much more likely to cross it. The SED in operation works similarly to a turnstile or cattle gate in a stockyard: The sequential lowering and raising of left, central, and right barriers induces a single electron to transit from left to right.
The subtle electric charge
In discussing the proposed redefinition of SI electrical units, I noted that metrologists want to check the exactness of the JV and QHR formulas, but I introduced the current formula I = fe as if it were above reproach. Is it clear, however, that the formula is exactly correct? In particular, is the discrete charge pumped through an SED turnstile exactly the same as a free electron in vacuum? Experiments dating back to Robert Millikan establish that in vacuum the charge of a free electron or an electron in an atom or ion is a fundamental constant that doesn’t depend on position or time. In an SED, though, the situation is more complex. For one thing, the electrons feel the effects of the underlying ionic background. Moreover, each electron strongly interacts with all the others, which means that the electrons are in a complicated many-body quantum state. Fermi liquid theory shows that in many cases the electrons’ low-lying excitations function as if the electrons are in single particle states, but at a fundamental level the simple picture of free conduction electrons is far from true.
Thus some years ago our team at NIST examined the possibility that the charge per cycle passed through a single-electron pump, a device similar to the turnstile described earlier, might have the modified value (1 + ɛs)e. To check, we used the SED pictured in figure 2 in a capacitance standard: We pumped N ≈ 200 million electrons onto a capacitor and related the capacitance to the voltage via C = QV. Since we are allowing for the possibility that the charge of the electron is different from its vacuum value, we set Q = N(1 + ɛs)e. In our experiment the capacitance is accurately measured and the voltage is an experimentally determined quantity. To the extent that ɛs = 0, the charge passed per unit cycle of the SED pump is equal to the charge of a free electron in vacuum. Our result is fortunately—or perhaps unfortunately, depending on how one views it—a null one: ɛs = (-0.5 ± 9.2) × 10-7.

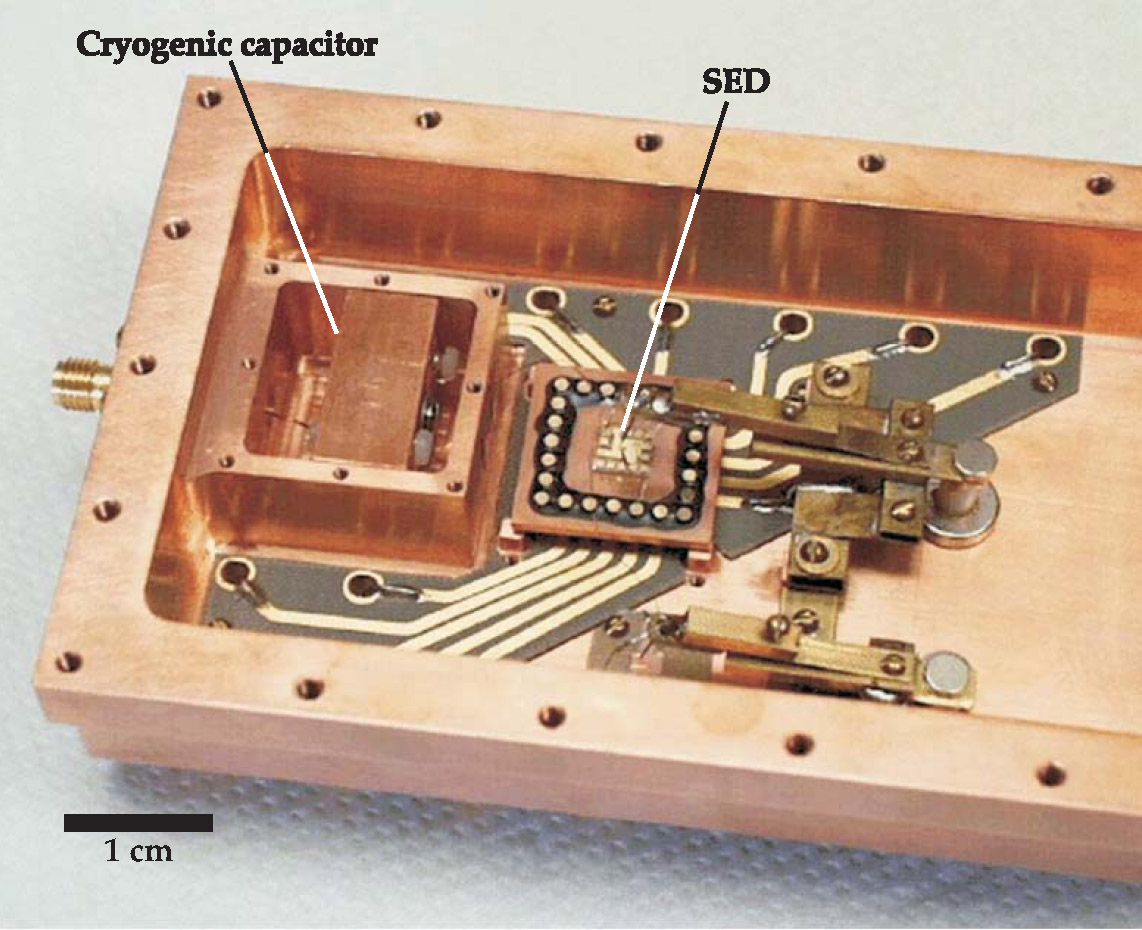
Figure 2. A single-electron device deposits individual electrons on a capacitor in this NIST experiment that addressed the question. Is the charge of an electron passed through an SED the same as the charge of the electron in vacuum? Voltage is applied to the SED along some of the gold leads visible in the photograph; other leads are related to current measurements. The brass switches to the right connect the cryogenic capacitor either to the SED at 0.02 K or to a well-calibrated, room-temperature capacitor.
(Courtesy of Mark Keller.)
Accurate metrology experiments have various other important implications for physics, including tests of quantum electrodynamics and of the value of the fine-structure constant. It is fascinating that the venerable field of standards, which dates back at least as far as Old Kingdom Egypt, still offers the potential for new discoveries in fundamental physics through its adaptation of modern technologies such as lasers, ultralow-temperature techniques, and nanofabrication.
It is a pleasure to acknowledge Mark Keller for his collaboration and Dave Newell for his careful review of this article.
It is a pleasure to acknowledge Mark Keller for his collaboration and Dave Newell for his careful review of this article.
References
1. M. W. Keller, “Current Status of the Quantum Metrology Triangle,” Metrologia 45, 102 (2008).
2. P. J. Mohr, B. N. Taylor, D. B. Newell, “The Fundamental Physical Constants,” Physics Today, July 2007, p. 52.
3. M. Tinkham, “Coulomb Blockade and an Electron in a Mesoscopic Box,” Am. J. Phys. 64, 343 (1996).
4. N. M. Zimmerman, “A Primer on Electrical Units in the Système International,” Am. J. Phys. 66, 324 (1998).
More about the Authors
Neil Zimmerman works as a research physicist at the National Institute of Standards and Technology in Gaithersburg, Maryland.
Neil M. Zimmerman. National Institute of Standards and Technology, Gaithersburg, Maryland, US .

