Mesmerizing magnetic fields

There is something mysterious, even a little unsettling, about magnetism, which is why magnets are such great toys for kids and so lucrative for charlatans. But magnetism has also provided a great deal of amusement for serious-minded folks who, over the course of time, have put it to work in countless ways. In the 19th century, scientists discovered that magnetism could be used to generate electricity, create electric motors, and transform voltages. Developments in the 20th century included magnetic memory, magnetic resonance, and magnetic medical imaging. Magnetic fields, researchers found, can also separate isotopes in cyclotrons and mass spectrometers, direct charged particles in accelerators, and levitate trains. Given all those applications, it seems remarkable that magnetism still has a few tricks up its sleeve.

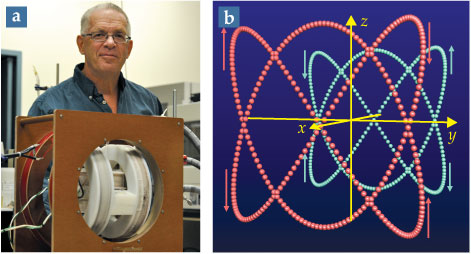
In our lab, the two of us use magnetism to make fluids flow, often in striking ways. Such noncontact flow eliminates the need for motors and impellers and the seals they employ. To create our magnetic fields, we combine two or three mutually orthogonal components, no more than one of which is constant, or DC. Figure 1a shows the device that generates the fields; it includes three mutually orthogonal pairs of nested Helmholtz coils. Running current through any Helmholtz pair generates within it an essentially uniform magnetic field parallel to its cylindrical symmetry axis. The two or three oscillating, or AC, components have frequency ratios that form simple rational numbers. A typical field might have one constant component and two oscillating components with frequencies of 200 Hz and 300 Hz. Figure 1b shows how that example field evolves in time.

Chains and checkerboards

Unless they are modified, liquids do not respond to magnetic fields. One approach is to add ions so that an applied voltage can create a current in the now conductive liquid. When a magnetic field is applied across the current, the resulting Lorentz force causes fluid motion. The study of such motion is called magnetohydrodynamics. A second approach is to add magnetic particles—typically either pure iron or a ferromagnetic oxide of iron—that magnetize and interact strongly in the presence of a field but retain little of that magnetization when the field is turned off. When the particles are large enough that they eventually settle out, the fluid is called a magnetic particle suspension.

In response to a static magnetic field, the particles in a magnetic suspension form chains that resist flow. That phenomenon, called magnetorheology, has applications to dampers and clutches. But when the field itself is persistently changing direction and magnitude, the suspension can be made to do marvelous things, such as form flow lattices, vortices, and vortex lattices. Those effects can be applied to generate efficient directed heat and mass transfer, fluid mixing, and active wetting. Moreover, with the right fields, magnetic suspensions can be induced to imitate complex biological behaviors.

Subjecting a suspension of magnetic platelets to a particular biaxial AC field produces the striking flow lattice shown in figure 2a, in which the columns are normal to the field and the flow along any given column is opposite to the flow in the neighboring columns. Unlike natural convection, this surprising “isothermal magnetic advection” requires neither a thermal gradient nor gravity, so it could be useful for heat and mass transfer in space. It is an emergent behavior—like the flocking behavior in a murmuration of starlings—that arises because the dynamic field induces torques and moments on individual platelets that couple to other particles. Stranger still is the configuration shown in figure 2b, a checkerboard lattice of counterrotating vortices. Such structures emerge when the platelet suspension is subjected to a triaxial field, such as shown in figure 1b, comprising a biaxial AC field and a single DC component.

Increasing the magnetic platelet concentration causes the flow lattice to rise up into a pronounced ridge. When the two components of the biaxial AC field have a particular evolving phase relation, the ridge oscillates back and forth along its length, alternately climbing opposing walls. That caterpillar-like behavior arises because of an oscillating bulk torque, imparted by the magnetic field, that is ultimately due to vorticity within the flow columns.

The vortex fluid

When a suspension of micron-sized spherical magnetic particles is exposed to the right kind of magnetic field, the result is a vortex fluid—that is, a fluid whose torque density is uniform throughout. Vortex fluids behave in remarkable ways. They can, for example, crawl up the side of a container; circulate around the walls of a glass vial to actively wet its surface, as shown in figure 2c; and simulate biological dynamics as described below.

The magnetic fields that generate vortex fluids always have three components, at least two of which are AC. Intuitively, it would seem that the field trajectory must have some kind of circulation, such as occurs for a rotating magnetic field. That is not so, but the field trajectory must have a type of reversibility, because it would be absurd if the laws of nature were to allow only clockwise or counterclockwise vorticity. In part because the field and its negative produce the same forces and torques in a system of induced magnetic moments, the actual condition for creating a vortex field is that the union of the trajectories for the field and its negative—for example, the combined turquoise and salmon structure shown in figure 1b—must have the same symmetries under 180° rotations as vorticity does.

To create a suitable magnetic field, one could first make a biaxial AC field whose frequency ratio could be expressed as a simple rational number. If, in reduced form, either the numerator or denominator is even, application of an orthogonal DC field induces fluid vorticity around the biaxial-field axis corresponding to the odd number in the ratio. (In the case of figure 1b, that would be around the z-axis.) Reversing the DC field reverses the flow. If the numerator and denominator are both odd, the vortex flow circulates around the DC field axis, and reversing the DC field doesn’t reverse vorticity. However, an appropriate phase change in either of the biaxial AC field components will reverse the vorticity. Because the DC component separates the planes of the field and its negative, we call the vortex-inducing fields with a constant field component “symmetry-breaking rational fields.”

A second way to create a field with the required symmetry is to create a triaxial AC field having rational frequency ratios such as 1:2:3. We call those “rational triad fields.” When the ratios are expressed in reduced form, the vorticity axis corresponds to the component having unique numerical parity, which is 2 in the 1:2:3 case. (For a fully odd reduction such as 1:3:5, the situation is more complicated.) The phases of the various field components can be adjusted to control the magnitude of the flow and whether it is clockwise or counterclockwise.

The driven vortex fluids exhibit biomimetic dynamics when immersed in a second, immiscible liquid. One particular torque-inducing field shreds the suspension into countless “buzzing bees.” Another causes the bees to swarm and nucleate a writhing serpent that strikes out and devours any bee foolish enough to wander by. The cannibalistic incorporation of bees into serpent represents a transition from one far-from-equilibrium state to another.

Other biomimetic dynamics suggest a slime mold and its constituent amoebas. The slime mold has a complex life cycle that starts with individual amoebas that move by projecting and retracting pseudopods. When the amoebas have trouble finding food, they aggregate into a slime mold that moves by a peculiar “streaming-strand” motion and devours any tasty organic matter in its path. The amoebas can also form slugs that crawl to find food. The videos accompanying the online version of this Quick Study show those biomimetic behaviors as well as the flow patterns illustrated in figure 2.

Once the slime mold exhausts its sources of food, the slugs rise to make a fruiting body that looks like a berry on a stem. The berry eventually ruptures, sending out spores that give rise to the next generation of amoebas. That we can’t yet do with magnetic suspensions, but we’ll continue to try.

Supplemental materials

• Mesmerizing magnetic fields: The flow lattice

When subjected to a biaxial oscillating magnetic field, a suspension of magnetic particles can organize into the flow lattice shown here. The flow along each column is up or down, in the direction opposite to its neighbors. Various defects cause the “writhing” black areas.

• Mesmerizing magnetic fields: The vortex lattice

When subjected to a triaxial oscillating magnetic field, a suspension of magnetic particles can organize into the lattice of counterrotating vortices shown here.

• Mesmerizing magnetic fields: Active wetting

Externally applied magnetic fields can induce a suspension of magnetic particles to wet a cylindrical surface. Note that the wetting flow can be readily reversed.

• Mesmerizing magnetic fields: Birth of a chaotic swarm

When a suitable magnetic field is applied to a suspension of magnetic particles (black) immersed in an immiscible liquid, the suspension will disintegrate into what appears to be a swarm of angry bees.

• Mesmerizing magnetic fields: The hungry serpent

Each of the black dots in this video represents a suspension of magnetic particles surrounded by an immiscible liquid. When an appropriate magnetic field is applied, swarming dots combine into a serpent-like shape that appears to gobble up the remaining dots.

• Mesmerizing magnetic fields: Dancing amoebas

When a suitable magnetic field is applied to a suspension of magnetic particles (black) immersed in an immiscible liquid, the suspension will carry out a rapid amoeba-like dance.

• Mesmerizing magnetic fields: Moving slime mold

The black fluid flowing up and down is a suspension of magnetic particles immersed in an immiscible liquid. The organized flow shown here, induced by a rapidly varying external magnetic field, is reminiscent of slime-mold locomotion.

• Mesmerizing magnetic fields: Slithering slugs

Each of the black dots in this video represents a suspension of magnetic particles surrounded by an immiscible liquid. When the right kind of magnetic field is applied, the dots move around like slugs and occasionally combine with others.