Elastic-wave propagation and the Coriolis force
DOI: 10.1063/PT.3.3408
In a coordinate system fixed with respect to the rotating Earth, the Coriolis force deflects an object sideways relative to its direction of motion. A beautiful demonstration of that effect is the Foucault pendulum, illustrated in figure
The time rate of change of the oscillation direction is given by

Figure 1. Rotating oscillation planes. The majestic Foucault pendulum (a) at the California Academy of Sciences knocks down pillars as its direction of oscillation (red double-headed arrow) rotates clockwise (blue arrow). (Photograph by Another Believer.) (b) This obviously not-to-scale sketch of a Foucault pendulum defines the parameters

Elastic-wave rays are not deflected
Earthquakes generate elastic waves—seismic waves—that propagate through Earth and scatter off places where material properties change suddenly, notably at the core–mantle boundary. Does Earth’s rotation leave an imprint on those waves? One might imagine that a ray lying along the propagation direction of an elastic wave would be deflected by the Coriolis force or that the polarization of the wave would be affected.
To investigate whether rays of elastic waves are deflected by Earth’s rotation, we (joined by Katsuhiko Shiomi; see the additional resources) used the seismometers of USArray, a seismic network that covers most of the US. We found that even eight hours after a major earthquake, elastic waves continue to propagate along the great circle defined by the earthquake site and the array. On the surface of a sphere, propagation on a great circle corresponds to straight-line motion in the plane.
During the eight hours separating earthquake and observation, Earth rotated by 120°. A deflection of the propagation over such an angle would easily have been observable. The absence of any deflection indicates that seismic rays corotate with Earth; in other words, the ray is not subject to the Coriolis force. Intuitively, the reason is that seismic waves are carried by a medium—the rotating Earth. The result follows formally from analysis of the equations governing rays in a moving medium. The behavior of electromagnetic waves, which are not carried by a medium, is significantly different: The direction of propagation of electromagnetic waves is not influenced by Earth’s rotation. For that reason, the interference of light in a ring laser can be used as a rotation sensor.
Shear-wave polarization rotates
Elastic waves can be longitudinal or transverse. Longitudinal waves are polarized along the direction of propagation. Those waves, called P waves, move faster than the transverse waves, also called shear waves or S waves. The polarization of P waves lies in the ray direction, and since the rays corotate with the Earth, the polarization of P waves does so as well. In brief, the polarization of P waves does not change in response to the Coriolis force.
For S waves, polarization is in a plane perpendicular to the propagation direction. In contrast to the case for P waves, the polarization of S waves does rotate. That rotation, like the rotation of the Foucault pendulum, is a classical manifestation of the Berry phase, which accounts for the way oscillations in a system change when the system is slowly transported around a circuit—for example, a circle of latitude.
The rate of change of an S wave’s polarization direction,
Big bounce, small polarization change
Measuring the change in S-wave polarization due to Earth’s rotation presents a challenge because transverse elastic waves do not propagate for long in a pure S-wave state. The candidates best suited for observation are so-called ScS waves—S waves that bounce once between Earth’s surface and the boundary that separates Earth’s core and mantle. Figure
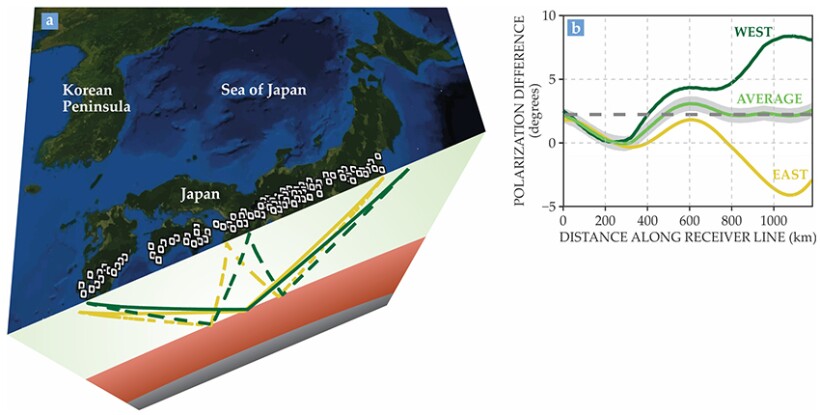
Figure 2. Measuring a rotating polarization. To determine the Coriolis-force-induced rotation of seismic-wave polarization, (a) we used the stations of Japan’s High Sensitivity Seismograph Network that are marked by the small squares. The yellow lines indicate the eastward-propagating trajectory of seismic waves generated by an earthquake near the west end of the array: The solid line is a trajectory of an ScS wave that bounces once off the core–mantle boundary and the dashed line is an ScS2 trajectory that bounces twice. Green lines signify the westward-propagating seismic waves created by an earthquake near the eastern part of the array. (b) Shown here is the measured difference in polarization between ScS and ScS2 waves for the eastward-moving (yellow) and westward-moving (green) trajectories described above. The light green curve is the average of the two trajectories; for a long distance along the receiver line, that average reveals the effect of the Coriolis force. The gray band shows our error estimate and the dashed line indicates the theoretical prediction for the long-distance average.
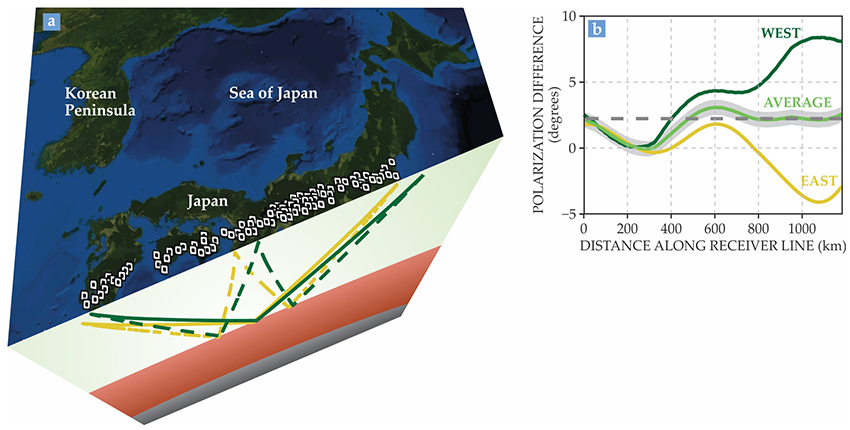
We used several tricks to achieve the required precision. First, we combined measurements of S waves recorded at stations of the High Sensitivity Seismograph Network (Hi-net) in Japan (figure
An additional complication is that the predicted polarization difference of 2.3° is comparable to the change in polarization that arises as rays are bent by inhomogeneities in Earth’s structure. The polarization change due to those inhomogeneities is opposite in direction for eastward- and westward-propagating waves. But the polarization change induced by the Coriolis force is always clockwise in the Northern Hemisphere, no matter the direction of propagation.
So for our third trick, we studied two earthquakes—the 2005 Tanegashima earthquake, which occurred on the western end of the Hi-net array, and the 2005 Miyagi earthquake, which occurred off the eastern end of the array. Figure
References
1. M. V. Berry, “Quantal phase factors accompanying adiabatic changes,” Proc. R. Soc. London A 392, 45 (1984). https://doi.org/10.1098/rspa.1984.0023
2. J.-P. Pérez, O. Pujol, “Two often disregarded aspects of Foucault’s pendulum,” Eur. J. Phys. 36, 015019 (2015). https://doi.org/10.1088/0143-0807/36/1/015019
3. H. Igel, M. Bernauer, J. Wassermann, K. U. Schreiber, “Seismology, Rotational, Complexity,” in Encyclopedia of Complexity and Systems Science, R. A. Meyers, ed., Springer (2015).
4. R. Snieder, C. Sens-Schönfelder, E. Ruigrok, K. Shiomi, “Seismic shear waves as Foucault pendulum,” Geophys. Res. Lett. 43, 2576 (2016). https://doi.org/10.1002/2015GL067598
More about the authors
Roel Snieder is a professor of geophysics at the Colorado School of Mines in Golden. Christoph Sens-Schönfelder is a researcher at the GFZ German Research Centre for Geosciences in Potsdam. Elmer Ruigrok is a senior seismologist at the Royal Netherlands Meteorological Institute in De Bilt.







