Earth flyby anomalies

Planetary flybys began to receive much attention during the 1960s, when NASA’s Jet Propulsion Laboratory (JPL) first started thinking about what would later become the Pioneer and Voyager missions—the grand tours of the solar system conducted during the 1970s and 1980s. The concept was to have the gravitational force of a planet give a “gravitational assist” to a satellite moving under the Sun’s influence, so as to change the satellite’s direction and speed as measured in a barycentric reference frame tethered to the center of mass of the solar system. At the time, many found it surprising that a planet could transfer energy to a spacecraft, even though Joseph Lagrange, Carl Jacobi, and Félix Tisserand had long since established that the energies of comets could be affected by passing near Jupiter. After all, they might have reasoned, isn’t the energy of a satellite flying through the solar system conserved?

Planetary flybys

When a third body such as a planet is considered, the energy of the satellite need not be conserved; only the total energy of the entire system must be constant. A flyby (see figure 1) can give kinetic energy to a spacecraft to boost its orbital velocity or even unbind it from the Sun’s gravitational tug, or it can take away kinetic energy to slow the craft down for an inner-body encounter.

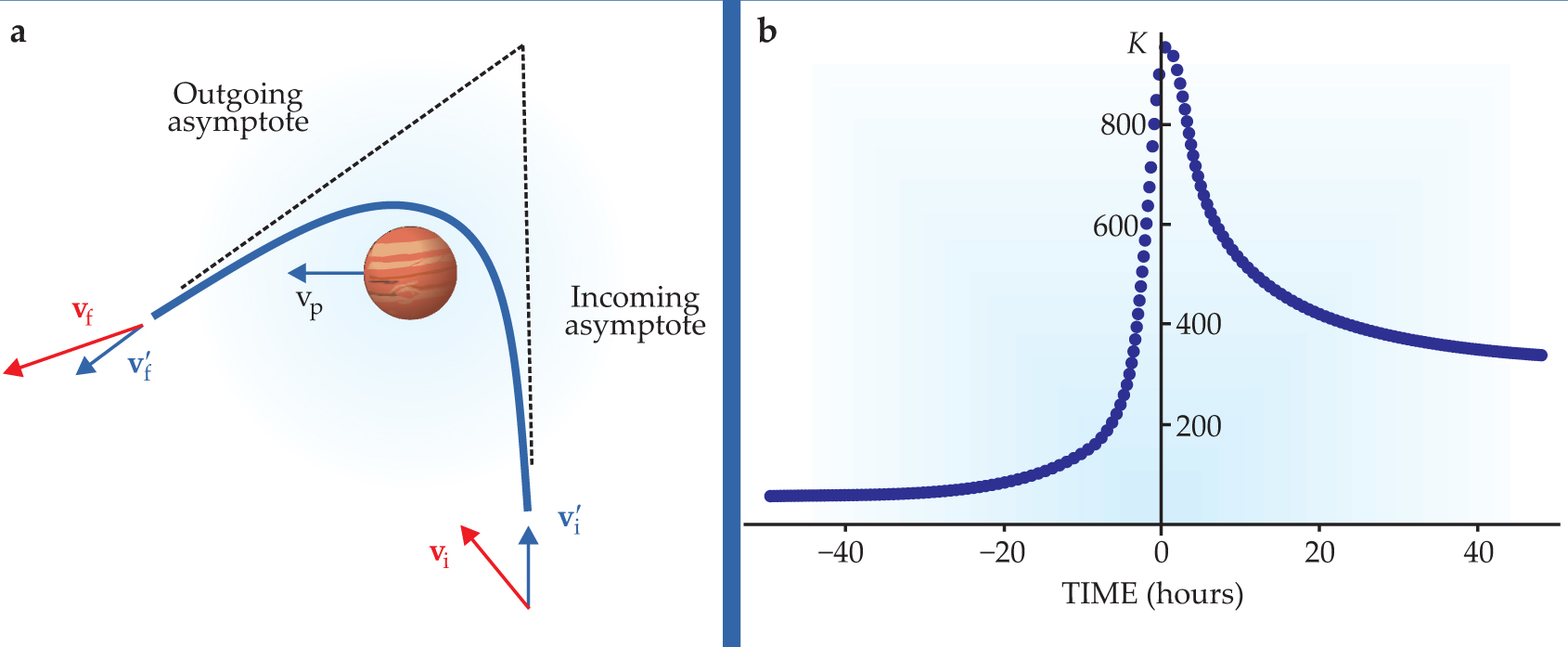
Figure 2(a) describes a two-body system—say, a planet and a satellite—orbiting the Sun. Let the velocity of the planet in the solar system be v _p (assumed constant) and the initial and final velocities in the planet-centered system be v _i’ and v’_f, respectively. The initial and final velocities in the barycentric system, v _i and v _f, are obtained by adding v _p to the velocities in the planet system. Although the initial and final kinetic energies are equal in the planet-centered frame, the change in kinetic energy per unit mass in the barycentric system, ΔK =[(v _f · v _f) – (v _i · v _i)]/2, is nonvanishing. A little algebra gives ΔK = v _p · (v’_f – v’_i).

Assume, for argument’s sake, that the planet is in a counterclockwise orbit around the Sun. Then, roughly speaking, if a satellite in the ecliptic (plane of the planet’s orbit) approaches from inside the orbit, travels behind the planet, and then goes around it counterclockwise as illustrated in the figure, kinetic energy will be added to the spacecraft. Conversely, kinetic energy will be taken from a spacecraft that comes from inside the planetary orbit, travels in front of the planet, and goes around it clockwise.

Of course, the system does not violate the law of energy conservation. The energy change—and, for that matter, angular-momentum change—is absorbed by the planet. However, for that massive body, the relatively tiny change is not noticeable. In this Quick Study we’ll take a more detailed look at the Pioneer 10 flyby and then discuss a surprising result associated with Earth flybys: A number of craft have exhibited a small change in speed such that the outbound hyperbolic orbits in the Earth-centered system have a different energy than do the inbound orbits.

Energy transfer in a Jupiter flyby

The Pioneer spacecraft were the first to probe the major planets of the outer system and to go beyond those planets. They have now been overtaken by the faster Voyagers, which are approaching the edge of the solar system, where interstellar magnetic fields dominate. Pioneer 10, launched on 2 March 1972, was the first craft to reach a giant planet—Jupiter, which it did on 4 December 1973. During its cruise from Earth to Jupiter, Pioneer 10 was bound to the solar system. With the Jupiter encounter, Pioneer 10 reached solar-system escape velocity.

Figure 2(b) illustrates the kinetic-energy transfer process during the Pioneer 10 flyby of Jupiter, as viewed in the barycentric frame. As Pioneer 10 approached Jupiter, it first gained a great deal of energy from the planet and then returned some back. Does that make sense?

Reconsider figure 2(a) and the dot-product expressions for ΔK. Those equations are asymptotic formulae. But they can be recast as time-dependent equations if one substitutes an intermediate-time velocity v’(t) for the asymptotic velocity v’_f. Then one has ΔK(t) = v _p · [v’(t) − v’_i]. The dot product with v’_i is a constant. The other dot product, as figure 2(b) shows, gives a spike just after Pioneer 10’s closest approach to Jupiter. As the satellite goes around the back side of the planet, v’(t) aligns with v _p. The maximum of ΔK is reached when v’(t) is parallel to v _p ; that occurs just after perigee. Then, as the satellite swings around further, v’(t) goes out of alignment with v _p and ΔK(t) decreases some.

Anomalous Earth flybys

The effect of an Earth flyby on a satellite depends on the bending of the spacecraft’s geocentric trajectory. As discussed above, that change in direction can cause either a decrease or increase in the spacecraft’s energy as measured in the barycentric frame, depending on whether the spacecraft encounters Earth on the leading or trailing side of its orbital path. But, when measured from Earth, the spacecraft’s energy should be the same before and after the flyby. The data indicate that such is not always the case.

Instead, for Earth flybys involving the Galileo, NEAR (Near Earth Asteroid Rendezvous), Cassini, Rosetta, and Messenger spacecraft, the final and initial energies were noticeably different. For example, Galileo 1’s asymptotic final speed was 4.13 ± 0.03 mm/sec greater than its asymptotic initial speed; other spacecraft had final speeds less than the initial speed. The changes, though typically only a millionth of the satellites’ cruising speeds, were much too large to be explained in terms of any conventional time-explicit cause—specifically, as arising from the nonsphericity of Earth or from the motions of the Moon and Sun. Moreover, for the Rosetta flyby, JPL and European Space Agency programs independently determined the satellite’s orbit. Thus the observed energy nonconservation is probably not due to code errors. So far, no one has identified a mechanism, either external or internal to the spacecraft, that can unambiguously produce the observed energy changes.

The mass distribution of Earth and the dynamics of flybys are supposedly well known, yet the transfer of energy remains puzzling. Is there at least some phenomenological pattern to the anomalies? Indeed, a phenomenological formula exists that, perhaps fortuitously, fits the anomalies—at least for those spacecraft whose altitudes were below 2000 km:

$$\begin{array}{c}\frac{\Delta {\upsilon }_{\infty }}{{\upsilon }_{\infty }}=K\left(cos{\delta }_i-cos{\delta }_{\text{f}}\right),\\ K=\frac{2{\omega }_{\oplus }{R}_{\oplus }}{C}=3.099\times {10}^{-6}.\end{array}$$

Here δ_i and δ_f are the initial and final declination angles, analogous to Earth’s latitude but measured on the celestial sphere; ω_⊕ is Earth’s angular velocity of rotation; R _⊕ is its radius; and c is the speed of light. With additional data, one might be able to generate a formula that also includes spacecraft achieving altitudes greater than 2000 km. But in any case, a phenomenological fit is not an explanation. What is the speed of light doing there? How does the declination produce a physical effect?

Given the anomalous energy transfer in Earth flybys, one might consider returning to the flybys of Jupiter and Saturn and looking for unexpected energy transfers there. Unfortunately, the uncertainties in the giant planets’ gravitational fields make that program untenable. In addition, given the speed of a flyby trajectory, detection of the relatively small anomalous speed changes would require that the spacecraft be free of unknown, systematic accelerations. Such accelerations can be generated, for example, by onboard systems or by atmospheric drag. To be useful for analyzing flybys, the Doppler-shifted data sent by the satellite must be of high quality and referenced to ground-based atomic frequency standards. That requirement limits the number of candidates for further flyby tests, whether of Earth or other planets. However, given the importance of the gravity-assist technique as a means for conserving rocket fuel, flybys will occur in the future, and we feel it is worth the effort to overcome the difficulties just discussed.

Several physicists have proposed explanations of the Earth flyby anomalies. The least revolutionary invokes dark matter bound to Earth. Others include modifications of special relativity, of general relativity, or of the notion of inertia; a light speed anomaly; or an anisotropy in the gravitational field—all of those, of course, deny concepts that have been well tested. And none of them have made comprehensive, precise predictions of Earth flyby effects. For now the anomalous energy changes observed in Earth flybys remain a puzzle. Are they the result of imperfect understandings of conventional physics and experimental systems, or are they the harbingers of exciting new physics?