Topological insulators: from graphene to gyroscopes
On 4 November, Charles Kane and Eugene Mele received the 2019 Breakthrough Prize in Fundamental Physics for their trailblazing work related to topological insulators. The University of Pennsylvania researchers published two papers in 2005 about the quantum spin Hall effect in graphene. They predicted that spin-orbit coupling would open a bandgap in graphene without an external magnetic field. As a result, the material would behave as a bulk insulator but with unidirectional conducting edge states corresponding to modes in the bandgap. Kane and Mele realized that graphene’s band topology protects those edge states, which puts it into a class of materials called topological insulators (see the article by Xiao-Liang Qi and Shou-Cheng Zhang, Physics Today, January 2010, page 33 ).
Now some researchers are looking beyond quantum systems to mechanical systems that also behave as topological insulators. By observing and tinkering with the emergent edge states in classical systems, researchers are investigating phenomena that also hold true in harder-to-manipulate quantum systems. Mechanical topological insulators could also lead to applications in controlling and directing the flow of energy, such as impact absorption, sound isolation, and acoustic lensing.
Research into expanding the scope of Kane and Mele’s insight first appeared in 2015, when Katia Bertoldi’s group at Harvard University and William Irvine’s team at the University of Chicago harnessed the behavior of topological insulators with a mechanical metamaterial. The researchers showed—through band structure calculations, simulations, and experiments—that a lattice of coupled gyroscopes could be used to replicate the behavior of quantum topological insulators.
A honeycomb lattice of coupled gyroscopes (diagram at left, experimental setup at right) is a macroscopic system that behaves as a symmetry-breaking topological insulator.
Lisa Nash, Noah Mitchell, William Irvine
Like a moving charge in a magnetic field, a gyroscope moves perpendicular to the force it experiences. For some lattice arrangements, the equations of motion describing the gyroscope displacements are not symmetric under a combined operation that reverses time and flips each gyroscope displacement across a common axis, thereby breaking symmetry under an operation analogous to quantum mechanical time reversal. Not every lattice is symmetry-breaking, so tuning the geometry can turn topological behavior on and off. When quantum time-reversal symmetry is broken, even if a wave moves around the lattice in one direction, it may not be able to do so in the opposite direction.
Mode analysis shows that a honeycomb lattice of masses connected by springs has a band of optical modes, where neighboring sites vibrate out of phase, and a band of acoustic modes, where all sites vibrate in phase. Replacing the masses with spring-coupled gyroscopes opens a gap between the two bands. When one of the gyroscopes is repeatedly prodded at a frequency that falls within that gap, a mechanical compression–relaxation wave propagates along the lattice edge but does not go into the bulk. And because of the broken time-reversal symmetry, the edge modes move only in one direction.
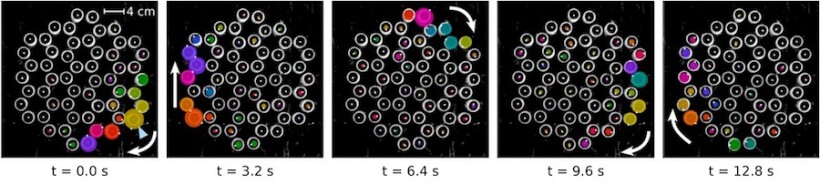
When the lower right corner of the gyroscope lattice is excited at a frequency in the bandgap, the lattice conducts vibrations in a single direction and only along its edge. Colors indicate the gyroscopes’ phase.
L. M. Nash et al., Proc. Natl. Acad. Sci. USA 112, 14495 (2015)
The researchers observed the predicted bandgap in simulations and experiments. Exciting the lattice at frequencies in the optical and acoustic bands caused waves to propagate in the bulk of the lattice, whereas excitation frequencies in the bandgap led to motions that were restricted to the boundary. Distorting the gyroscope lattice is analogous to changing the magnetic field in the quantum system. By doing so, the researchers were able to change the direction of the vibrations’ propagation along the edge.
The topology leading to protected edge modes is not the topology of the lattice itself. If that were the case, regular masses and gyroscopes would have the same behavior. The material’s interesting properties come instead from the topology of its band structure in momentum space. When a band is topologically nontrivial, waves pick up an extra phase instead of returning to the same state when they evolve through a closed loop in momentum space. The lattice structure is still important, but only because it determines the band topology.
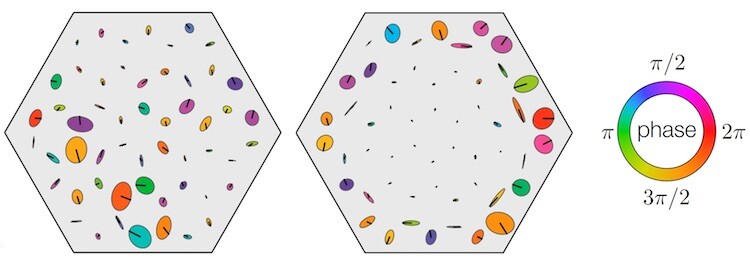
When the gyroscope lattice is excited outside the bandgap, the vibrations go into the bulk (left). When it is excited in the bandgap, the vibrations travel along the edge with a periodically varying phase (right). Ellipses indicate the gyroscope trajectories.
L. M. Nash et al., Proc. Natl. Acad. Sci. USA 112, 14495 (2015)
Such a hands-on system has “offered rapid prototyping and a superior level of access to the individual components,” says Noah Mitchell, a researcher in the Irvine Lab in Chicago. That control has allowed the group to explore phenomena beyond those seen in quantum systems. For example, the researchers recently demonstrated a controlled topological phase transition in which they turned the protected edge modes on and off in real time using external magnetic fields.
By systematically reorganizing the gyroscopes, the researchers in Chicago found that topological behavior goes beyond just being insensitive to disorder : the protected edge modes exist not only in disordered lattices but even in completely amorphous structures with no underlying lattice. According to Mitchell, this work predicts “the existence of glassy topological insulators in electronic materials, photonic materials, acoustic resonators, and beyond.” Such topological insulators, which have random instead of crystalline structures, “challenge the traditional bond between order and topology.”