Thermodynamics Explains the Symmetry of Spherical Viruses

If a virus succeeds in planting its genome in a cell, the cell is doomed. Forced to follow the genome’s orders, the cell makes the enzymes needed to replicate the genome and the proteins that constitute the viral coat. From coat proteins and replicated genomes, new, identical copies of the virus spontaneously assemble. The cell bursts, the viruses escape.

Outside its cellular host, the viral genome would disintegrate without the protection of its coat, the capsid. But if the capsid were too strong, the infectious genome would be trapped inside. Could that balance be upset to defeat virus-based diseases? New research from UCLA into capsid structure suggests it could. ¹

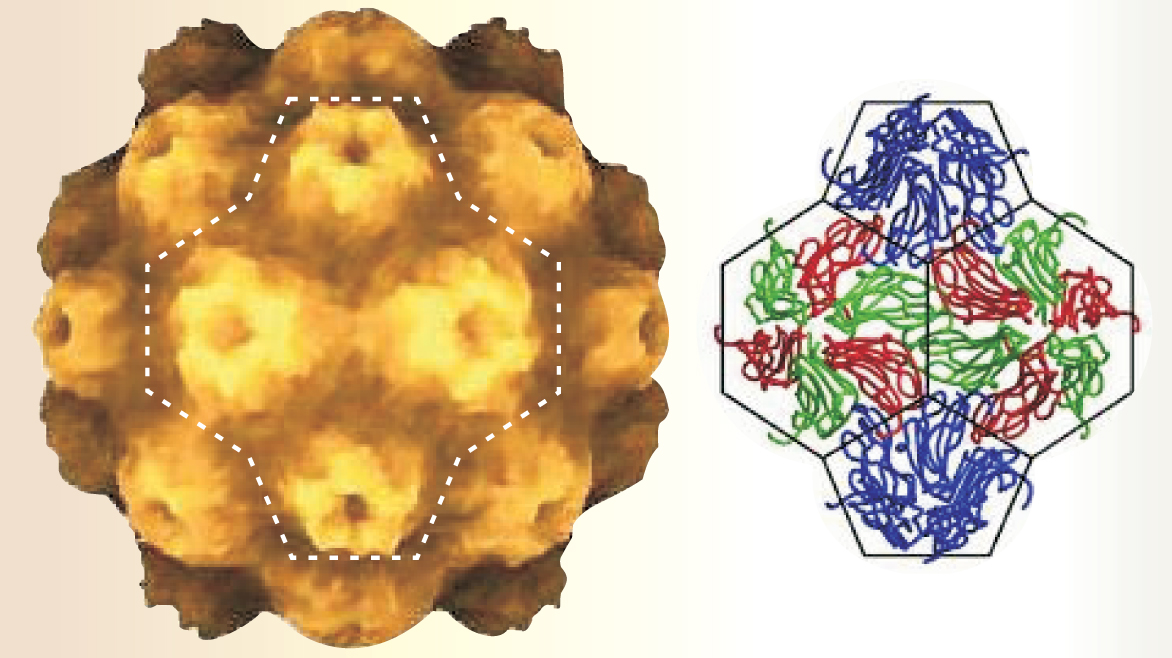
As determined by x-ray and electron crystallography, capsids are highly symmetrical, especially those of small, spherical viruses, such as poliovirus, norovirus, and the turnip yellow mosaic virus (TYMV) shown in figure 1.

In 1956, armed with little more than an observation of capsid symmetry and the knowledge that proteins by themselves are asymmetrical, Francis Crick and James Watson made a bold proposal. ² The capsids of spherical viruses, they reasoned, are made up of “the regular aggregation of smaller asymmetrical building bricks.” By considering the topology of space and the geometry of tiling, Crick and Watson concluded that capsids must adopt the symmetry, but not necessarily the structure, of one of the five Platonic solids: the tetrahedron, the cube, the octahedron, the dodecahedron, or the icosahedron.

Better data revealed that spherical capsids overwhelmingly choose icosahedral symmetry. With 20 triangular sides, the icosahedron has twofold, threefold, and fivefold symmetry and the largest volume-to-surface ratio of the Platonic solids.

In 1962, Donald Caspar and Aaron Klug devised a mathematical rule for generating icosahedral capsid structures. ³ Their building bricks are capsomers: regular polygonal groupings of capsid proteins. According to Caspar and Klug, one makes a capsid by placing a pentameric capsomer on each of the 12 vertices of the icosahedron that lie on one of the six fivefold symmetry axes. Then, one fills the space between the pentameric capsomers with hexameric capsomers of the same side length. The bigger the capsid, the more hexameric capsomers one can fit—but only in the proportion of 12 pentamers to 10(T − 1) hexamers, where T = h ² + k ² + hk and h and k are nonnegative integers.

Soccerballs qualify as capsid structures. Their pentagonal and hexagonal panels have the same ratio, 12:20, and are distributed in the same way as the pentamers and hexamers of TYMV.

Is it any wonder?

Though not strictly alive, viruses have optimized their survivability through adaptation. If icosahedral structures maximize the volume enclosed by a shell of identical units, is it any wonder viruses choose it?

As figure 1 shows, the proteins that make up a hexameric or pentameric capsomer, like other proteins, are messy strings of amino acids. Capsomer proteins vary widely from virus to virus. Yet somehow, even in a test tube, the proteins of a particular virus reliably self-assemble to form a capsid whose structure is drawn from Caspar and Klug’s simple, predetermined menu. To UCLA’s Robijn Bruinsma, William Gelbart, and Joseph Rudnick, such a generic process looks like free-energy minimization—that is, physics.

When the UCLA team began investigating capsid assembly four years ago, modeling the kinetics of capsid assembly molecule by molecule was intractable. It still is. So, rather than ask how capsids form, they sought the physical origin of icosahedral symmetry.

As a first step, they considered a curved two-dimensional system of identical disk-shaped capsomers that interact on the surface of a sphere. The Hamiltonian for such a system includes the restriction that capsomers can’t overlap, along with an adhesion energy arising from the tendency of capsomers to join up and minimize the exposure of their edges to water.

Calculating the Hamiltonian’s minima yielded some of the Caspar and Klug structures, but not all of them, and it yielded some nonicosahedral structures, too. The UCLA researchers conjectured, but didn’t prove, that Caspar and Klug’s sequence could be recovered by including 12 smaller disks in the Hamiltonian to play the role of the pentamers. ⁴

Monte Carlo

Two years ago, Roya Zandi and David Reguera joined the UCLA team and, in Zandi’s words, “took the model more literally.” They replaced the no-overlap restriction with a more realistic Lennard-Jones potential that accounts for both repulsion and attraction. And rather than mandate the presence of pentamers, they gave capsomers the choice of switching between pentameric and hexameric states. In real life, the structural difference between the two capsomer shapes arises from the gain or loss of a capsid protein. But in the new version of the model, the switch, which takes place at an adjustable energy cost ΔE, changes the disk radius by the appropriate geometric factor.

Other model ingredients include a capsomer–capsomer binding energy ε₀ of 15 kT (the value comes from lab experiments; at 30°C, it’s about 400 meV or 36 kJ/mol) and a Boltzmann ratio of hexamers to pentamers of exp(−ΔE/kT).

The modifications wouldn’t fit conveniently in an analytic approach, so Zandi and Reguera adapted the model for Monte Carlo simulation. ¹ In each run of the model, a fixed number N of capsomers slid about on a sphere. The aim was to derive the optimal capsid energy spectrum.

Figure 2 shows how the energy per capsomer varies with N for two cases: ΔE = 0 (black curve) and |ΔE| ≫ kT (blue curve). The overall downward slope of both curves reflects the tighter packing possible for larger capsids. But it’s the minima that dictate which structures predominate.

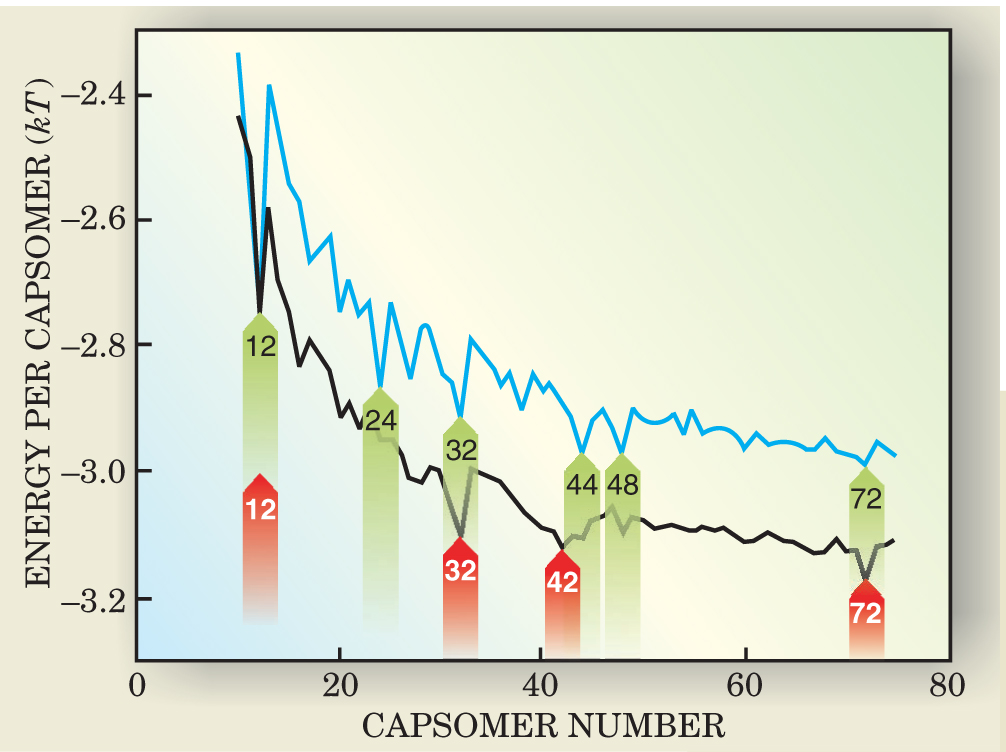
To see why, consider a capsid that has just one more capsomer than the number M at a minimum. If the percapsomer energy of the M + 1 capsid exceeds that of the M capsid by δε ₀, then the population of M + 1 capsids will be lower than that of the M capsids by the factor exp(δε ₀ M/kT). Even when δ is a few percent, that factor is huge: 10²³ for the minimum at 72.

Both spectra in figure 2 exhibit minima. For the case when pentamers and hexamers interchange without cost, the minima correspond to Caspar and Klug’s sequence. The first four of these structures appear in the left-hand side of figure 3, including TYMV’s N = 32.

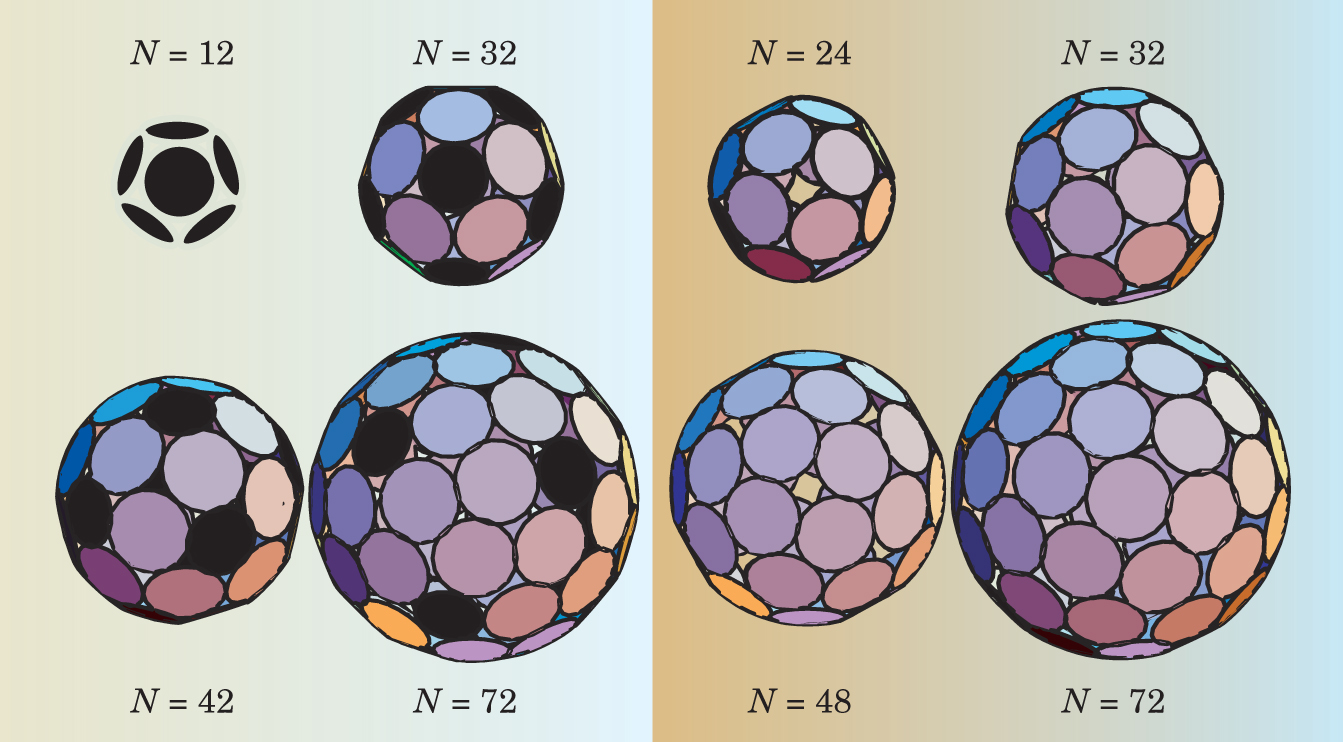
When |ΔE| ≫ kT, things change. The minima are more numerous and don’t necessarily correspond to Caspar and Klug’s sequence of icosahedral structures. Two of them, N = 24 and N = 48, have octahedral symmetry; N = 44 has cubic symmetry; and N = 72 can adopt several symmetries, including icosahedral.

The nonicosahedral capsids don’t enclose the largest possible volume for their surface area, yet they are stable. Why does nature avoid them? To reproduce, a virus must reliably land in the same free-energy minimum over and over again. The ability of capsomer proteins to form pentamers and hexamers with equal ease spreads out the free-energy minima, making them easier for evolution to find.

Most antiviral agents follow one of three strategies: block the receptor that mediates the entry of the virus into the host cell, thwart the action of viral enzymes, or provoke the body’s immune system to attack an infected cell before it releases its brood of viruses. Interfering with capsid assembly offers an alternative strategy. For example, one could divert the assembly of a capsid toward a structure of nonicosahedral symmetry. Such a capsid, being the wrong size, would no longer provide the right, tight fit for the genome.

An antiviral agent would work at the molecular level, a scale below the disk-shaped capsomers of the UCLA model. But such models, says Adam Zlotnick of the University of Oklahoma Health Sciences Center in Oklahoma City, provide a foundation for more detailed approaches.