Parisi shares Nobel Prize for breakthroughs in understanding disordered systems

The development of mathematical tools for understanding many-particle systems was one of the greatest achievements of 19th-century science. Extracting macroscopic properties of a gas by tracking the random motions of each individual atom remains an impossible feat. Statistical mechanics provided a framework for properly averaging over the individual particles’ motions and understanding how they lead to collective macroscopic properties such as temperature and pressure.

But disorder takes many forms. Whereas gas molecules bouncing around a bottle sample the phase space of possible positions and velocities, the molecules that make up that glass or plastic bottle are frozen in disarray, trapped far from equilibrium. Explaining how those disordered molecules ended up stuck in a particular configuration and how that connects to any macroscopic properties is currently beyond the reach of statistical mechanics.

Giorgio Parisi is to receive half of this year’s Nobel Prize in Physics for finding order in seemingly disordered complex systems. Among other significant contributions, he solved a model of a particular type of disordered system, spin glasses. ¹ “By attacking the problem analytically and being able to solve it, he found a different paradigm for what ordered phases can be,” says Leticia Cugliandolo, a professor at Sorbonne University in Paris. The underlying structures he found have helped researchers tackle seemingly intractable problems in neural networks, hard-sphere jamming, and protein folding, among other research areas.

A frustrating puzzle

Dilute magnetic alloys were created in the 1950s to experimentally study interactions between magnetic ions. They consisted of a few magnetic atoms dispersed in a nonmagnetic material—for example, manganese in zinc oxide. When impurity levels were low, the materials behaved as expected. But when the concentration of magnetic ions reached a few percent, measurements of the materials’ magnetic susceptibilities and specific heats as functions of temperature yielded features that suggested a phase transition.

As in a ferromagnet, a magnetic alloy’s spins become frozen in a particular configuration below a certain critical temperature $T_{\mathrm{c}}$. But whereas a ferromagnet’s spins are aligned, those in alloys were seemingly random (see the article by Daniel S. Fisher, Geoffrey M. Grinstein, and Anil Khurana, Physics Today, December 1988, page 56 ). That frozen disorder led to the alloys being called spin glasses.

The randomness in spin orientations arises because the ions’ positions are randomly distributed and their interactions can be ferromagnetic or antiferromagnetic. Those constraints make it impossible to minimize all the interaction energies simultaneously, and the spins are said to be frustrated (see the article by Roderich Moessner and Art Ramirez, Physics Today, February 2006, page 24 ). Without a best configuration, the system ends up in one of the many seemingly random good-enough options.

Accounting for the properties of spin glasses piqued the interest of theorists, notably Philip Anderson and Sam Edwards. (Anderson wrote a seven-part column in Physics Today about the history of spin-glass research that includes more detail than this story; the first installment appeared in the January 1988 issue on page 9 .) Compared with other disordered systems, such as structural glasses and polymers, spin-glass systems seemed as though they might be amenable to a simple and solvable model because their disorder is baked into their fixed interactions.

In 1975 Anderson and Edwards used the random Heisenberg Hamiltonian, $H=\sum J_{ij}{\mathbf{S}}_i·{\mathbf{S}}_j$, to describe an arrangement of spins ${\mathbf{S}}_i$ that can point in any direction. ² The interaction strengths $J_{ij}$ decrease with separation and, importantly, can take on both positive and negative values, thereby encompassing both ferromagnetic and antiferromagnetic spin pairings.

Calculating the system’s thermodynamic properties required averaging the logarithm of its partition function $Z$ over many sample configurations. To do it, Edwards devised the replica method, which involved taking the average of many versions of the system—replicas—that have the same interaction matrix $\mathbf{J}$. The model yielded a cusp in the magnetic susceptibility at the phase transition, in agreement with experiments. It also produced features not seen in experiments, including a cusp in the specific heat.

To gain more insight, David Sherrington and Scott Kirkpatrick simplified the model further. ³ They gave the spin interactions infinite range, thereby creating a mean-field model, and replaced the Heisenberg spins with Ising ones that could point in only two directions, up and down.

The simplification hoisted a glaring red flag: negative entropy. Says Sherrington, “There is a known pathology for classical continuous variables that when you go to zero temperature, the entropy can become negative.” The negative entropy seen at zero temperature with Heisenberg spins should have disappeared with discrete Ising spins. The persistence of negative entropy in the Sherrington–Kirkpatrick model indicated a serious problem.

Unexpected structure

The culprit was replica-symmetry breaking. ⁴ Edwards and Anderson had assumed, correctly, that below $T_{\mathrm{c}}$ a particular spin’s orientations in different replicas $\alpha$ and $\beta$ would be correlated—meaning $q_{\alpha \beta }=⟨{\mathbf{S}}_i^{\alpha }·{\mathbf{S}}_i^{\beta }⟩$ was nonzero for $\alpha \ne \beta$. But they also presumed that any two replicas would yield the same result, $q_{\alpha \beta }=q$, after they averaged over all the spins. In fact, the situation was more complicated.

How the symmetry was broken, however, remained unclear. “The problem was hanging around with various people trying to think, What had we done wrong?” says Sherrington, a professor emeritus at Oxford University. “And that’s where Parisi came out of the blue with this fantastic new idea, which solved the problem.” His mathematical approach, published ¹ in 1979, fixed the negative entropy issue. It also enabled predictions of spin-glass properties, such as magnetic susceptibility, that turned out to be correct.

“He found a mathematical solution of the problem, much more advanced than the previous one,” says Hélène Bouchiat, a director of research at the Laboratory of Solid-State Physics, a joint research unit of the CNRS and the University of Paris-Saclay. “Mathematicians, I think, thought he was completely crazy.” To calculate the system’s free energy $F=-k_{\mathrm{B}}T\ln (Z)$, where $Z$ is the partition function, Parisi and others followed Edwards and Anderson’s strategy of using the identity $$\ln Z=\underset{m\to 0}{\lim }\frac{Z^m-1}{m}\text{.}$$ But in the spin-glass problem, $m$ is the number of replicas, and researchers struggled with the implications of sending that value to zero.

Undeterred, Parisi forged ahead into the zero-dimensional space where the matrix containing the spin correlations $q_{\alpha \beta }$ resided. (Those correlations appear in the calculation of $Z$.) The analytic procedure he devised for dealing with such objects produced a stable and consistent description of the Sherrington–Kirkpatrick spin glass. Although the deeper meaning of the approach is still not fully understood, the solution’s accuracy has since been rigorously validated.

A phase transition is normally accompanied by a change in an order parameter—a value characterizing the system’s degree of structure—usually from zero to nonzero. In a ferromagnet, that value is the magnetization, which is produced by spins aligning below $T_{\mathrm{c}}$.

Parisi’s order parameters $q_{\alpha \beta }$, of which there are infinitely many, instead measure the amount of overlap between two states. As expected, comparing a state with itself yields the largest overlap, $q_0=q_{\alpha \alpha }$. But surprisingly, as Parisi and his collaborators showed in 1984, the overlaps between the rest of the seemingly unconnected states weren’t random. ⁵ The most similar nonidentical states had overlap $q_{\alpha \beta }=q_1<q_0$, followed by $q_2<q_1$ for the next-closest states, and so on.

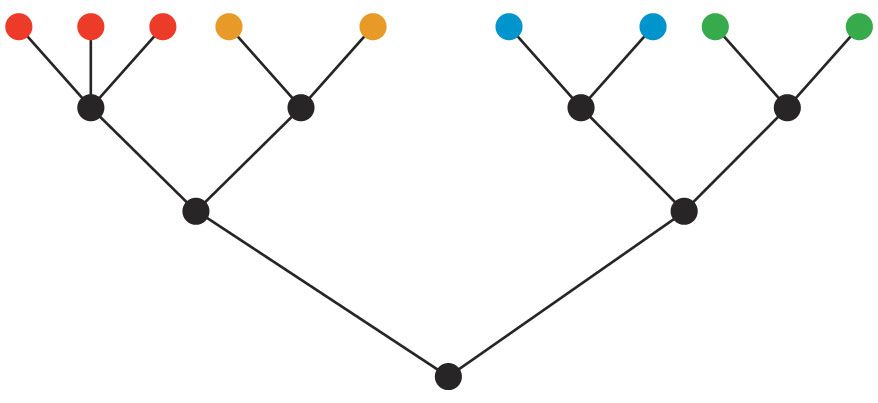
As illustrated in figure 1, the set of overlaps is ultrametric in structure—they satisfy the strong triangle inequality, $q_{\alpha \gamma }<\max (q_{\alpha \beta },q_{\beta \gamma })$. The number of nodes between two states reflects their amount of overlap. For example, any two states of the same color in the figure have the same amount of overlap, $q_1$. A red and an orange state have the next-highest overlap, $q_2$, the same as a blue and a green state. The branches of the ultrametric tree appear as the system is lowered below $T_{\mathrm{c}}$ and divide further and further as the temperature decreases—a reflection of the free-energy landscape becoming increasingly rugged, with more and deeper minima to trap the system.

Figure 1.

The spin-glass cornucopia

In simulations to investigate the zero-temperature entropy and other observables in spin glasses, Sherrington and Kirkpatrick encountered an obstacle: Once a spin glass settled into a local minimum, they couldn’t efficiently explore its rugged free-energy landscape for other stable states. From that starting point, changing just a handful of spins always increased the system’s free energy, leaving it on the steep slope surrounding the minimum. Parisi’s solution made it possible to show that the energy barriers between states grew with $N$, the total number of spins. Any effort to systematically search the landscape of a many-spin system would be futile.

Still, real-world and simulated spin glasses manage to form in a wide variety of stable states. And heating a system into its disordered phase and then recooling it allows it to fall into different minima without getting stuck in a particular one. Repeating that enough times, Kirkpatrick realized, would map the landscape.

Using that insight he, Daniel Gelatt, and colleagues demonstrated that such simulated annealing could be applied to other problems of combinatorial optimization—that is, finding the best solution from many possibilities. ⁶ One example they considered was the “traveling salesman” problem, which involves finding the shortest route a salesman could take to visit $N$ cities, each exactly once, and then return home (see figure 2a). The number of possible routes is on the order of $N!$, which quickly becomes intractable for even the most powerful computers. But even with thousands of cities, simulated annealing almost always effectively and efficiently finds the optimal solution, or at least a nearly optimal one.

Figure 2.

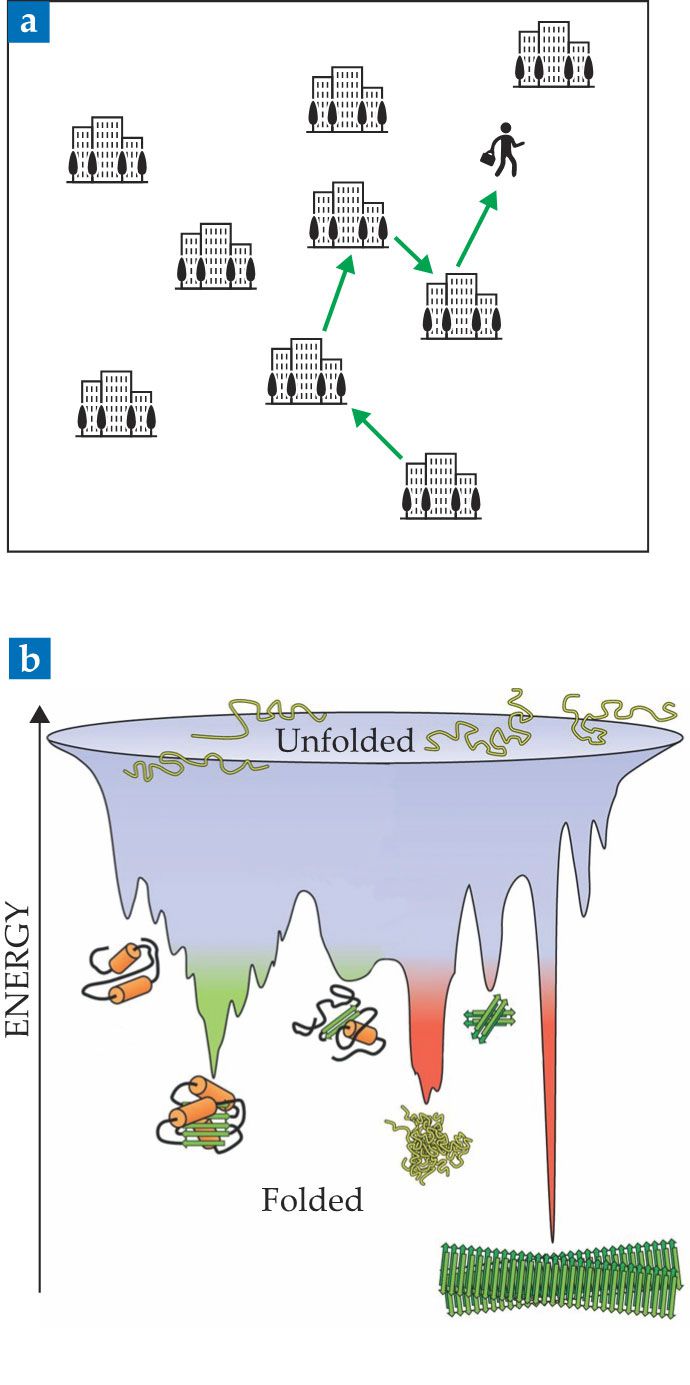
The traveling salesman problem is just one of many combinatorial optimization problems, some of which are of significant practical importance. Air-travel routes, supply-chain networks, computer-chip design, and distribution logistics all require solving similarly complicated problems. Biological problems such as finding folded protein configurations (see figure 2b) also benefit from such search techniques.

In the early 1980s John Hopfield, then a neuroscientist at Caltech, was studying neural networks—neurons connected by synapses—and how their collective behavior could result in phenomena such as memory formation. With neurons and synapses taking the place of spins and their interactions, respectively, Hopfield’s network had a form that closely mirrored that in the Sherrington–Kirkpatrick model. The ultrametric structure of the solutions can also describe patterns in memory formation, in both people and computers.

Applying Parisi’s formulation to Hopfield’s model was a gateway for many theorists. “To those of us who knew about spin glasses, there was a great deal of similarity with what we’d been working on, and the opportunity to move in that direction,” says Sherrington.

A natural question is whether spin-glass techniques can be applied to more ubiquitous structural glasses. Although some of the same ideas are relevant, namely disorder and frustration, the more familiar glasses have an added level of complication: Their disorder is not quenched. Once a spin glass’s magnetic moments are in place, their interactions are fixed. But the components of other glassy systems—be they molecules, grains, or biological materials—move around as they approach a glassy state, so their interactions are always evolving.

“In a sense, the ruggedness of the free-energy landscape of the fragile glasses is even more complex than for the spin glasses,” says Cugliandolo. Still, they share many properties, and some of the same tools can be applied. Parisi and his collaborators have used the replica method to exactly solve structural-glass problems in infinite spatial dimensions. Their mean-field solutions show that such glasses have a so-called Gardner transition, a nonequilibrium phase transition regarding the structure of free-energy basins, that was first identified in spin glasses by Elizabeth Gardner in 1985.

The cavity method, an iterative process developed by Parisi, Marc Mézard, and Miguel Virasoro as a mathematical alternative to the replica method, has been applied algorithmically to problems in constraint satisfaction, information theory, and other areas. Indeed, a wide range of fields that deal with complex interaction networks have benefitted from spin-glass concepts and methods, including economics, ecology, and evolution. ⁷ And the list continues to grow.

A universal scientist

Parisi’s work on spin glasses and replica-symmetry breaking has contributed to the understanding of complex and disordered systems in a range of fields. But, says Cugliandolo, “He has worked in so many different branches of physics and made important contributions to all of them, so I think this was also very important in the award.”

With researchers pursuing more siloed and specialized problems, it’s increasingly rare to hear about physicists making such broad contributions. But as a field theorist, Parisi has found wide-ranging applications for his skills. “He’s mentored a huge number of people who have gone all over the world and made great contributions in many different fields,” says Andrea Liu, a professor at the University of Pennsylvania in Philadelphia. “He’s very encouraging to people and works with students really well.”

Parisi first made a name for himself in quantum chromodynamics, the study of interactions between quarks and gluons. He and Guido Altarelli developed a quantitative description of inelastic scattering among quarks and gluons; their 1977 paper on that work is Parisi’s most cited. ⁸

Perhaps the clearest connection between Parisi’s contributions and the other half of the Nobel Prize recognizing climate modeling (see page 14 of this issue) is his work on stochastic resonance and turbulence. ⁹ He and his collaborators found that in nonlinear systems, just the right amount of noise combined with periodic forcing can generate a positive feedback loop and unexpected behavior. In particular, solar radiation and noise from oceanic and atmospheric dynamics cause large, seemingly paradoxical periodic temperature variations on the order of 10 °C.

Parisi’s willingness to tackle complex problems has led him to make many fundamental contributions, and his Nobel Prize celebrates that type of work. “These are ideas that come from physicists working in the way that physicists do,” says Sherrington. “If he hadn’t been working on very basic things, asking these very interesting questions, you wouldn’t have gotten to the other places that have been so useful.”