Month-long calculation resolves 82-year-old quantum paradox
DOI: 10.1063/1.3226702
In 1927, during the formative years of quantum mechanics, Friedrich Hund posed a paradox: Why is a chiral molecule found in either its left-handed or right-handed isomeric forms and not in a superposition of the two? After all, both isomers are equally likely and the molecular Hamiltonian is parity-invariant.
At first glance, the answer seems clear. If the tunneling time between the two isomers is long, their superposition is unlikely to arise. That answer might hold for a sugar, protein, or other large chiral molecule whose tunneling time may exceed the age of the universe, but it fails for ammonia and other small molecules. Nor can it explain why the habitual states of a molecule, large or small, are its left-handed and right-handed isomers and not its parity eigenstates.
Now, Klaus Hornberger of Ludwig-Maximilians University in Munich and his postdoc Johannes Trost have resolved Hund’s venerable paradox. 1 The two theoreticians analyzed the case of one of the smallest chiral molecules, dideuterium disulfide (D2S2; see figure 1), tumbling in and buffeted by a monatomic gas, helium. The calculation uncovered a surprisingly large phase dependence in the scattering amplitude that distinguishes the two isomers. Thanks to the phase dependence, the ambient gas atoms can pick out the molecule’s left-handed and right-handed isomers far more readily than the molecule’s other states. Even at low temperature and pressure, the effect of the He atoms colliding again and again with D2S2 is to knock the molecule into a chiral state and keep it there before it has a chance to tunnel out to its mirror image.

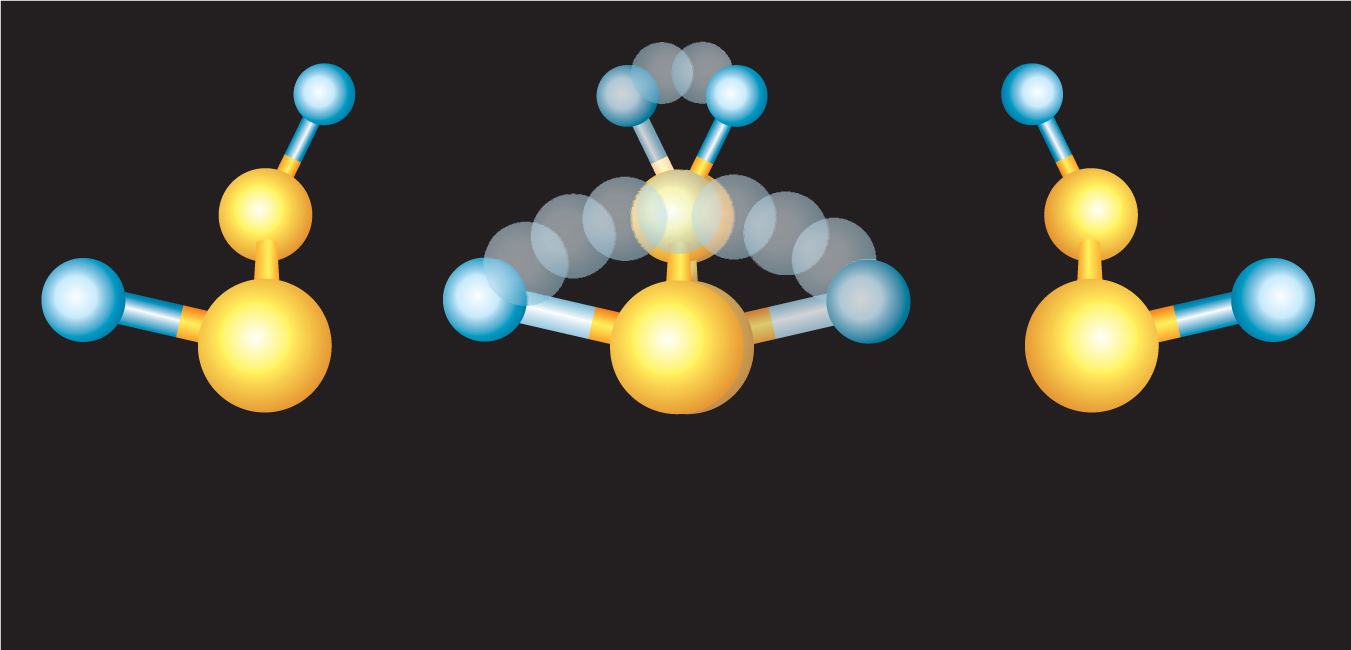
Figure 1. Dideuterium disulfide exists in left-handed (left) and right-handed (right) forms, thanks to its spatial arrangement of deuterium atoms (blue) and sulfur atoms (yellow). In principle, D2S2 can also exist in a superposition of the two isomers (middle).
(Adapted from I. Thanopulos, P. Král, M. Shapiro,
In one sense, Hornberger and Trost’s result is rather mundane: If you take proper, quantum account of how atoms collide with molecules, you derive the expected result, a mix of left-handed and right-handed isomers. But that mundanity is profound. The transition from a quantum superposition to a classical state arises not when some mysterious size threshold is breached but when the system’s interaction with its environment exceeds a calculable level of intensity. Decoherence theory, as that envirocentric view is known, is vindicated.
Chiral molecules and decoherence theory have been linked from the theory’s earliest days. One of the theory’s pioneers, Dieter Zeh, first discussed chiral molecules 2 in 1970 in support of a theory for grappling with the quantum-to-classical transition and other quantum measurement problems: Hugh Everett’s many-worlds interpretation of 1957.
Zeh’s 1970 discussion was qualitative. In 1981 Robert Harris and Leo Stodolsky tackled Hund’s paradox quantitatively. 3 They showed that long tunneling times alone can’t always explain the existence of chiral isomers. Unlike Hornberger and Trost, Stodolsky and Harris presumed the existence of—but didn’t identify—a parity-dependent scattering term that stabilizes the isomers and they didn’t couch their theory in terms of the then-nascent decoherence theory.
Zeh and coworker Erich Joos returned to the problem of chiral molecules in 1985. 4 They proposed the change in polarization of scattered photons as the parity discriminator. Unfortunately, their numerical calculations showed the interaction was too feeble. On the other hand, their order-of-magnitude estimate of a different parity discriminator, scattering by air molecules, suggested that a superposition of left-handed and right-handed chiral states would stabilize into one or the other isomer within a nanosecond.
By the time Hornberger became interested in Hund’s paradox in 2007, books on decoherence theory featured the problem as an outstanding one. Hornberger’s starting point was a master equation he developed based on work in the mid-1980s by Rolf Dümcke. A master equation is a set of first-order differential equations that describe the time evolution of a system’s probability of occupying each of a discrete set of states. Hornberger’s master equation applies to the general case of a quantum system (a rotating molecule) interacting with an environment (thermalized gas atoms) through a microscopically realistic, nonperturbative treatment of scattering.
For the case of a chiral molecule, the master equation yields an expression for the state-to-state decoherence cross section, η. When multiplied by the gas density and velocity and summed over all final states, η yields the rate γ at which a state decoheres. Crucially, the expression for η contains the difference between the scattering amplitudes of left-handed and right-handed states, |L〉 and |R〉. By symmetry the scattering amplitudes are equal in magnitude, but they can differ in phase. In that case, η is nonzero and γ is finite.
A parity eigenstate decays at the rate γ; the chiral states, which have the option of tunneling from one to the other, decay at a different rate, ω 2 /γ, where ω is the tunneling frequency. When γ ≫ ω, |L〉 and |R〉 persist, while the parity eigenstates quickly fade away.
To quantify that outcome for the case of D2S2 in He gas, Hornberger had to identify a chirality-dependent scattering interaction that leads to a finite phase difference. The leading term in the scattering, the dipole–dipole van der Waals interaction, is parity-invariant, but the next-largest term, the dipole–quadrupole interaction, does depend on chirality. And, as Hornberger discovered, it’s surprisingly large.
Keeping track of the phase for each state-to-state coupling proved arduous. Even at the modest temperature of 10 K, 100 or so rotational and orientational states are in play, which requires that 1000 equations be solved simultaneously. To meet that challenge, Hornberger and Trost had to develop almost from scratch a new numerical method. Grinding through the equations numerically took Trost a month. For temperatures above 10 K and on up to room temperature, the number of accessible states is so large that numerical calculation becomes infeasible. To cope with that regime, Hornberger and Trost developed an analytic approximation.
The top panel of figure 2 shows the scattering cross section summed over all the states, σtot. The bottom panel shows the corresponding decoherence cross section, ηtot. When obtained by numerical calculation, σtot and ηtot both exhibit peaks and troughs that arise from Feshbach resonances and other couplings between initial and final states.

Figure 2. How readily dideuterium disulfide adopts one of its chiral isomers when bombarded by helium atoms can be quantified by comparing the collision cross section σtot (upper panel) and the decoherence cross section ηtot (lower panel). Even at 5 K, ηtot is as much as 1/10 of σtot, indicating that chiral isomers stabilize quickly. Hornberger and Trost’s numerical calculation becomes too arduous above 10 K; the red lines correspond to an analytic approximation. The cross sections have units of the Bohr radius squared.
(Adapted from ref. 1.)
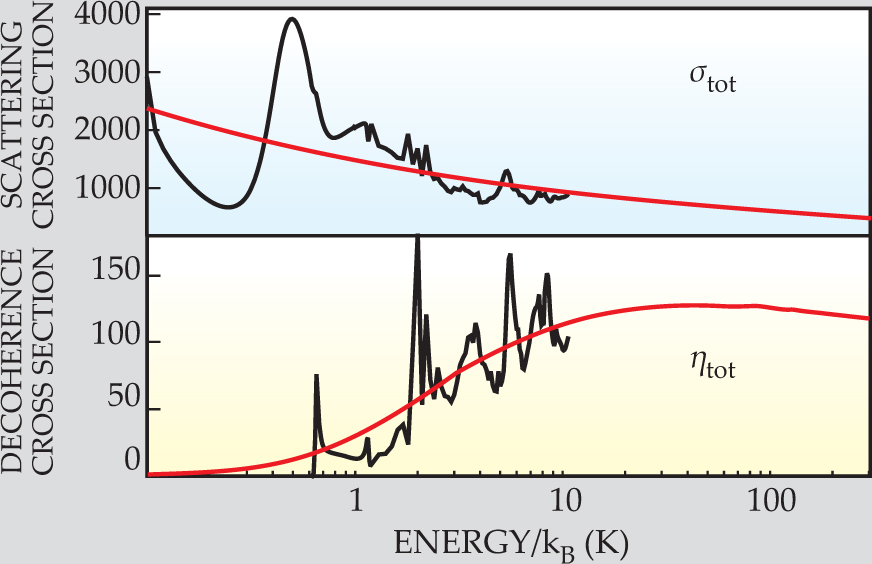
What matters is not so much the fine features in σtot and ηtot, but the two cross sections’ relative sizes. The ratio σtot/ηtot corresponds to the number of collisions that take place in one tunneling period before the molecule settles into one of its chiral states. Even just above 1 K, only 10 or so collisions suffice to knock the molecule into a chiral state. Above 10 K, when the high-energy approximation takes over, σtot/σtot saturates.
Hornberger chose to calculate the case for D2S2, rather than the lighter, cheaper H2S2, because the deuterium isotope, being heavier, has a longer and experimentally more convenient tunneling period (5.6 ms). He and Trost predicted that the pressure at room temperature, at which there are just enough He atoms to stabilize D2S2, is 1.6 × 10−5 mbar.
That prediction, the two theorists point out, could be tested by creating two initially pure beams of left-handed and right-handed D2S2 isomers. If both beams travel the same distance through vacuum, they can be expected to acquire superpositions that would lead, on detection, to an equal and opposite mix of left-handed and right-handed isomers. That result would still be the same if one of the beams passed through a gas cell containing He below the predicted critical pressure. Above the critical pressure, the final mixes would no longer be equal and opposite.
The |L〉 and |R〉 states of D2S2 are examples of what Wojciech Zurek, another pioneer of decoherence theory, calls pointer states. In the abstract language of the theory, the environment constantly monitors a quantum system, probing its states. The states that most readily give up information to the environment—the pointer states—are the most stable. Through a detailed analysis of one system, Hornberger and Trost have now recast that concept in the more concrete language of atomic physics.
References
1. J. Trost K. Hornberger, Phys. Rev. Lett. 103, 023202 (2009). https://doi.org/10.1103/PhysRevLett.103.023202
2. H. D. Zeh, Found. Phys. 1, 69 (1970). https://doi.org/10.1007/BF00708656
3. R. A. Harris L. Stodolsky, J. Chem. Phys. 74, 2145 (1981). https://doi.org/10.1063/1.441373
4. E. Joos H. D. Zeh, Z. Phys. B: Condens. Matter 59, 223 (1985). https://doi.org/10.1007/BF01725541




