Magnetic Resonance Force Microscope Locates a Single Electron Spin Inside a Glass Slab
DOI: 10.1063/1.1809083
Xrays, thanks to their short wave-lengths, can probe the shapes of proteins and biomolecules. But a single protein molecule can’t withstand a blast of high-energy photons for long enough to yield atom-scale structural information. To circumvent this limitation, structural biologists array countless copies of a protein in a crystal. Sharing the radiation dose, each molecule survives to contribute to the protein’s diffraction pattern.
Unfortunately, many proteins are expensive to produce in the large, pure quantities needed to make crystals. And many proteins defy crystallization altogether. Electron diffraction can coax structural information from small disordered samples, but so far not with atomic resolution and not from individual molecules. Other structural methods—neutron diffraction and nuclear magnetic resonance—demand samples that are large, crystalline, or both.
In 1990, the University of Washington’s John Sidles set himself the problem of locating the atoms in a single protein molecule. He sought a low-energy excitation whose origin in a molecule could be pinpointed. His solution, published as a concept, was to combine magnetic resonance (MR) with force microscopy. 1 MR provides the signal by manipulating electron or nuclear spins in the sample; the force microscope provides the detection.
Sidles settled on force microscopy because the performance of induction coils, the detectors in conventional MR, scales unfavorably with size. At least 1012 nuclear spins are needed to yield a detectable signal. Shrinking the coil to encompass fewer spins pushes the signal irretrievably below the noise.
By contrast, a force microscope becomes more sensitive as you make it smaller. Sidles realized that a magnetic resonance force microscope (MRFM), though then impracticable, was physically feasible. He persuaded Dan Rugar and Nino Yannoni of IBM’s Almaden Research Center in California to develop the idea.
Electron spins are easier to detect than nuclear spins because an electron’s magnetic moment is 658 times stronger than a proton’s. By 1992, the IBM team had used an MRFM to detect the combined signal of 1012 electron spins. Two years later, the team detected 1014 nuclear spins. Further advances followed and other groups, now numbering about a dozen, joined the MRFM quest.
Now, Rugar and his IBM colleagues Raffi Budakian, Benjamin Chui, and John Mamin have put the MRFM concept through its most stringent test yet: locating a single isolated electron spin. 2 Although the spin belonged to an artificially produced defect in a block of glass, its detection, says Chris Hammel of Ohio State University, is a real coup.
At a few attonewtons (10−18 N), the force exerted by an electron spin on an MRFM cantilever is a million times weaker than the forces encountered in atomic force microscopy. Detecting such a feeble force requires a floppy cantilever, but a floppy cantilever, unlike stiffer AFM cantilevers, can’t be positioned close to a surface lest the tip stick. As figure 1 shows, IBM’s cantilever is held perpendicular to the sample surface and deflects when a spin lies in front or behind rather than directly below. A laser interferometer records the deflections.
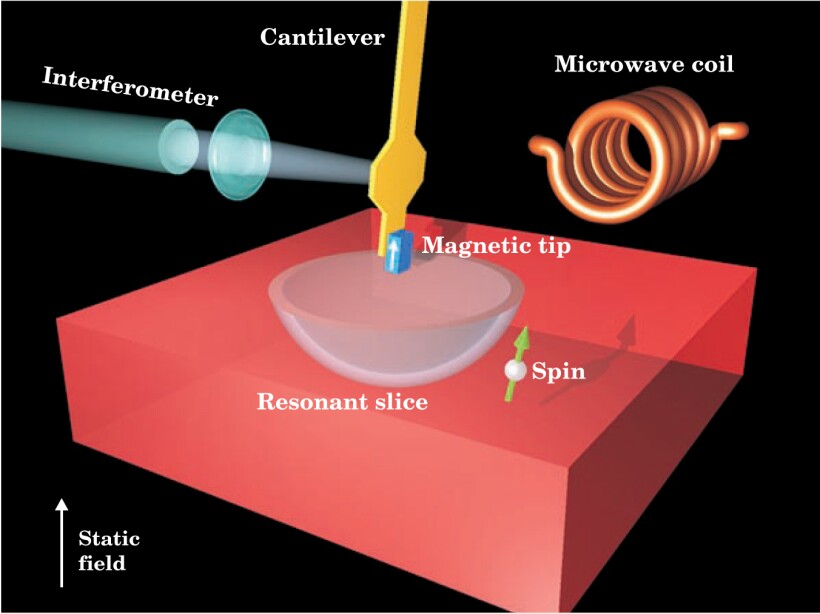
Figure 1. A vibrating cantilever scans across a sample. When a spin finds itself within the resonant slice, it draws energy from the oscillating field and flips. The flip causes a tiny shift in the cantilever’s vibration frequency, which is recorded by the laser interferometer.
(Adapted from ref. 2.)
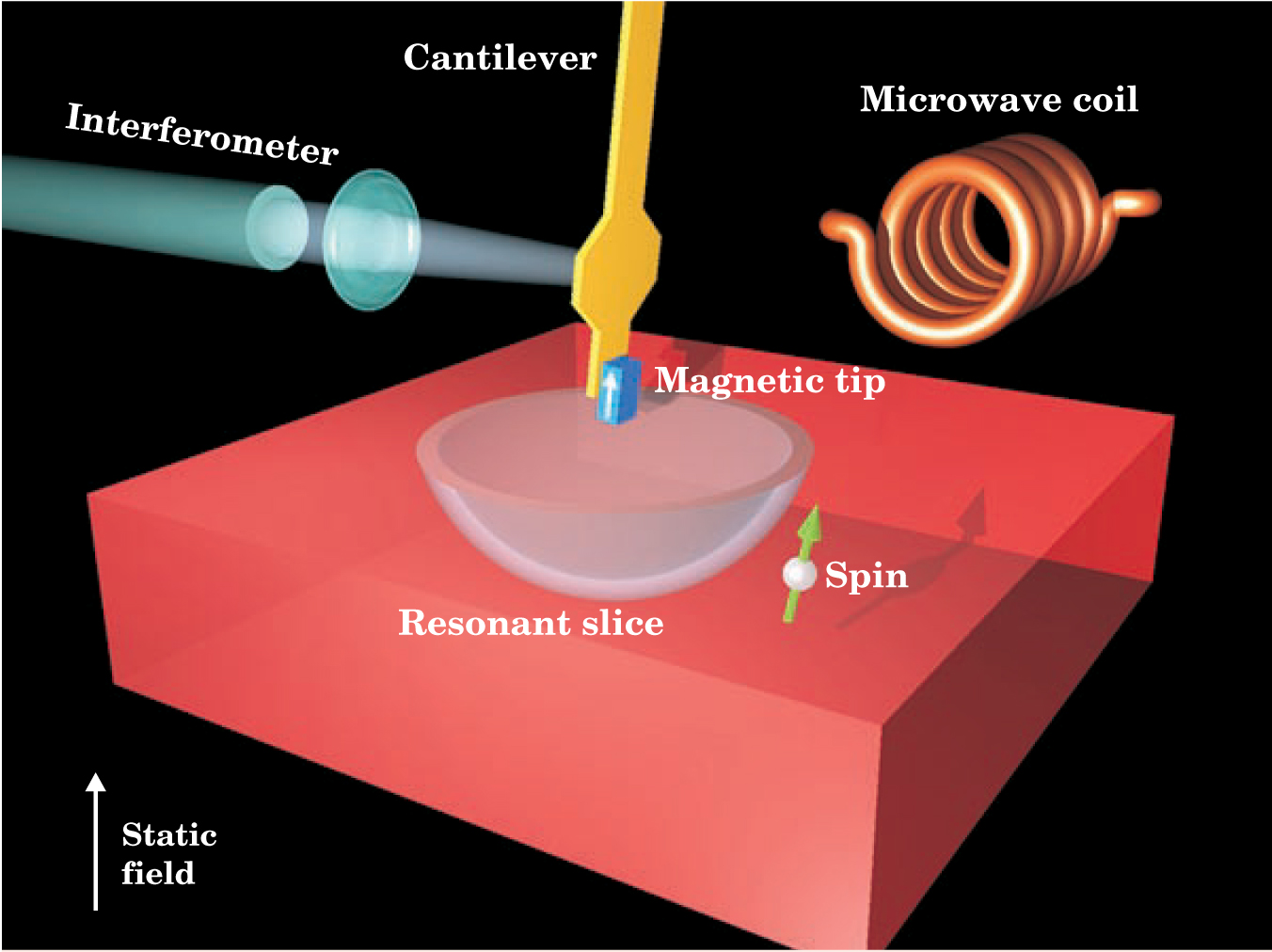
The MRFM detection scheme uses three magnetic fields: a weak oscillating field, a strong static field, and the field of the cantilever’s magnetic tip, which, thanks to the tip’s sharpness, has a steep gradient. Spins flip in a thin, bowl-shaped region where the splitting caused by static and tip fields resonates with the oscillating field. Sweeping this “resonant slice” through the sample locates the flipping spins.
The tip’s sharpness, and hence its field gradient, determines both the MRFM’s spatial resolution and its sensitivity. In his original paper, Sidles analyzed an MRFM’s limiting sensitivity µmin and found that µmin = (m eff T/τg 2)1/2. Here, g is the tip’s magnetic gradient and m eff, T, and τ are, respectively, the cantilever’s effective mass, operating temperature, and damping time.
Since the early 1990s, various MRFM groups have steadily improved cantilever performance. Fabricated from single-crystal silicon, the IBM cantilever is about 85 µm long, 100 nm thick, and weighs 90 picograms. The tip, a lump of samarium cobalt, delivers a gradient of 2 G/nm. Experiments are done within a dilution refrigerator at about 1 K.
How the cantilever is operated is as important as its properties. When it scans a sample, the IBM cantilever is set vibrating by a feedback loop at its mechanical resonant frequency of 5.5 kHz. Any spin that lies in the path of the resonant slice will flip up and down in time with the cantilever. If, after each flip, the spin and field are left parallel, the repulsive force between the two will quicken the cantilever’s vibration. If the spin and field are left antiparallel, the attractive force will slow the vibration.
That change—a jump or drop in vibration frequency when the cantilever nears a spin—is un-detectable amid the noise caused by far stronger electrostatic and van der Waals forces that tug on the tip. To make the signal stand out, the IBM team turns off the oscillating magnetic field every 64 cycles for exactly half the cantilever’s vibration cycle at precisely the point when the cantilever is at full swing. Deprived of resonant energy from the oscillating field, the spin misses a beat of its up-down-up-down rhythm. When the field is turned back on, an initially parallel spin will end up antiparallel and vice versa.
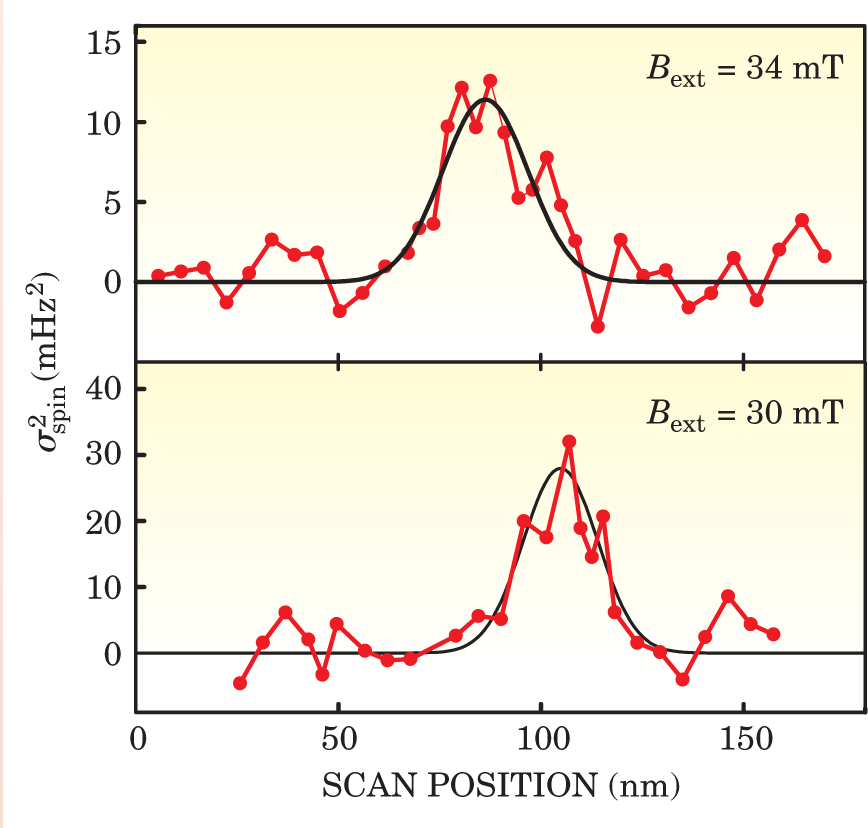
That syncopation introduces a weak, square-wave signal of frequency shift into the stream of data from the interferometer. Careful data analysis teases out the signal, but only after considerable signal averaging. To detect a single electron spin, the IBM team operated its cantilever for 13 hours. Figure 2 shows the result: a 5-standard-deviation signal that localizes the spin to 25 nm.
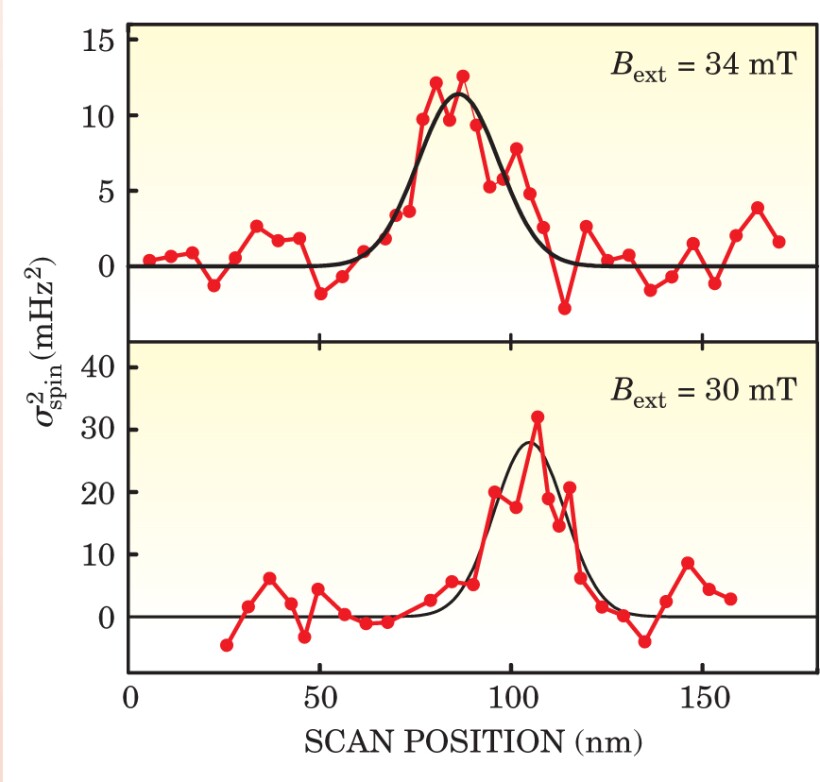
Figure 2. A peak in the spin signal reveals the position of the spin along the scan axis. Reducing the strength of the static magnetic field from 34 mT (top scan) to 30 mT (bottom scan), displaces the resonant slice and the spin’s apparent position.
(Adapted from ref. 2.)
As a test sample, the IBM team created a dilute system of single electron spins by irradiating a block of glass with a weak beam of gamma rays. The gammas displace electrons and leave sparsely spaced dangling bonds called E’ centers.
Not knowing where the spins were, Rugar and his team not only detected a spin but found it too. To make sure, they reduced the static magnetic field, thereby displacing the resonant slice and, with it, the separation needed between tip and spin. The result, shown in figure 2, was a shift in the apparent position of the spin.
The quantum nature of MRFM brings with it challenges and opportunities. If a spin relaxes too quickly when flipped, it can’t push or pull the cantilever for long enough to produce a measurable effect. In previous experiments, Rugar had observed an apparent acceleration of spin relaxation when the tip neared the sample surface. Uncorrected, the effect would have prevented the detection of a single spin. Fortunately, a quantum mechanical analysis by several groups revealed the culprit, the cantilever’s high-order vibrational modes, and a solution, modifying the tip.
Although biomolecules were the original inspiration for developing MRFM, other groups are working to apply it to other systems, notably the buried, irregular interfaces found in polymer systems. There, the absence of order means that a single small set of numbers, derived from diffraction, can’t fully describe the material’s structure. An atom-scale image would be ideal.
But to reach either goal—polymers or proteins—requires detecting protons and the nuclei of carbon, oxygen, and so on. Having improved the sensitivity of MRFM by 12 orders of magnitude to see one electron spin, Rugar is optimistic about obtaining the next three orders of magnitude to see a single proton spin.
References
1. J. A. Sidles, Appl. Phys. Lett. 58, 2854 (1991). https://doi.org/10.1063/1.104757
2. D. Rugar, R. Budakian, H. J. Mamin, B. W. Choi, Nature 430, 329 (2004). https://doi.org/10.1038/nature02658




