Ultimate turbulent thermal convection
DOI: 10.1063/PT.3.5341
Thermally driven turbulent flow can be found throughout nature and technology. Such flow transports not only heat but also mass and momentum. Comprehending what determines that transport is key to understanding numerous geophysical and astrophysical flows and to being able to control the industrial and more general flows that people experience every day.

The plume structure is visible in this numerical simulation of a sheared, thermally driven, turbulent Rayleigh–Bénard cell, viewed at a shallow angle above the cell’s lower plate. Colors denote the variations in temperature. (Courtesy of Alexander Blass, University of Twente.)

Geophysical flows include the transport of heat in the atmosphere and the ocean, which determines weather, climate, ocean circulation, and the melting of ice shelves. Astrophysical examples include the transport of heat in the core and in the outer layer of stars and planets. Industrial examples include the transport of heat in chemical reactors and in electrolysis and other contexts of energy conversion. At the human scale, people most directly experience heat transport in the buildings, rooms, and vehicles whose temperature they control.
In all those systems, the fundamental question is, How much heat, mass, or momentum is transferred by the system? Direct measurements are difficult to make, as the geometries are often complicated, heat may leak out of the system, the boundary conditions may not be well known or well controlled, and global measurements may not be possible, given the length scales of the systems. What’s more, direct numerical simulations may be prohibitive if the exact experimental boundary conditions are unknown.
Given those difficulties, the aim should be to understand real systems by using simple model systems, from which one can extrapolate the transport properties to the relevant flows. But developing those models requires a deep understanding of the system. That is especially true when the system undergoes a transition from one state to another—from a laminar-like state to a turbulent one, for instance—as then the transport properties of the flow can dramatically change. It is thus key to identify possible transitions between different states in such systems.
The most famous and most frequently used model to study thermally driven flows is the Rayleigh–Bénard (RB) system. It consists of a flow in a closed box of height
Figure 1.

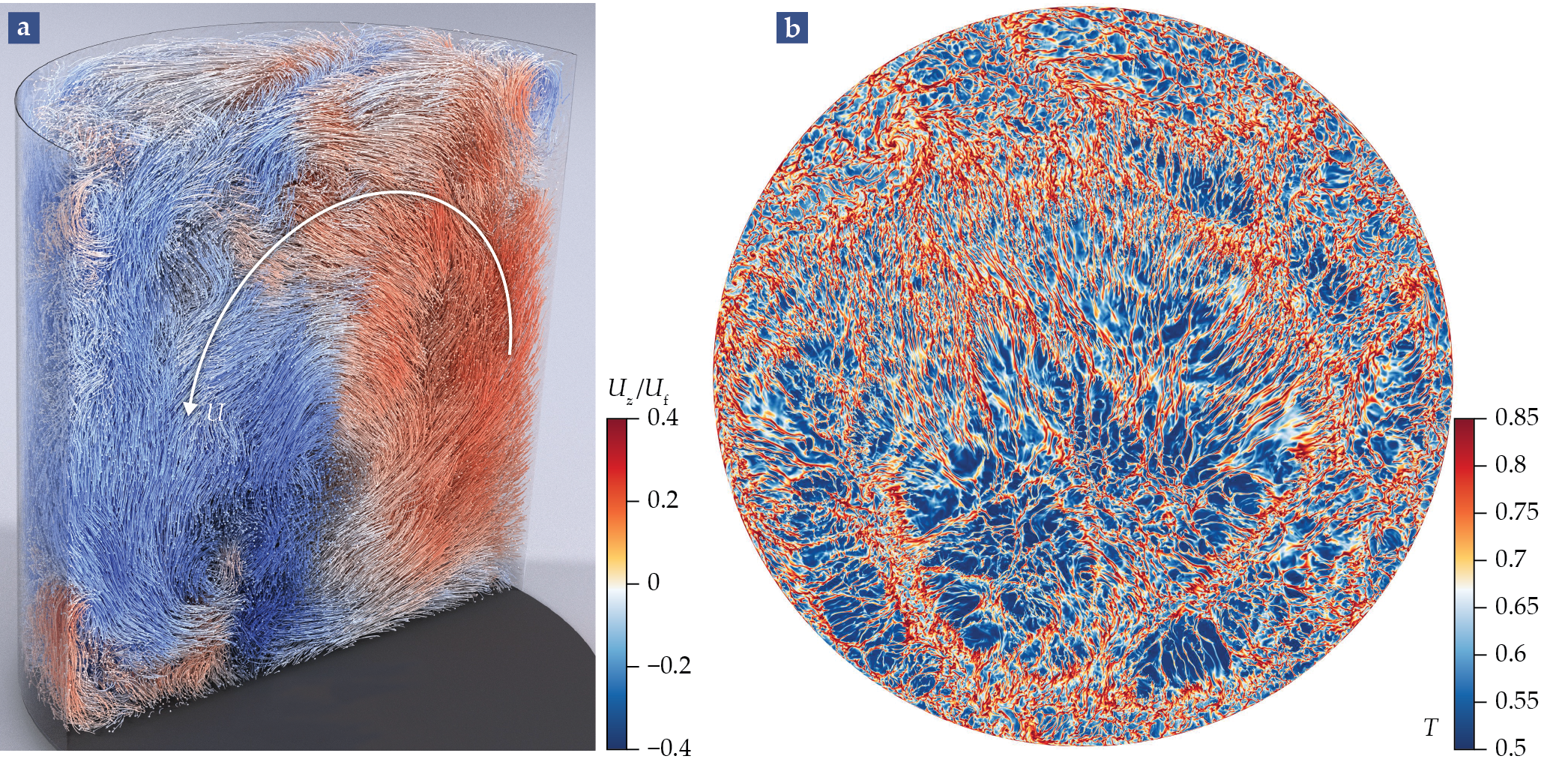
Three-dimensional visualization of experimental turbulent structures (a) in half of a cylindrical Rayleigh–Bénard cell with diameter-to-height aspect ratio
RB convection has always been a popular playground in which to develop new concepts, such as instabilities, nonlinear dynamics, and the emergence of spatiotemporal chaos and patterns. 1 For very weak driving, the system has few degrees of freedom—it can be described using few coupled ordinary differential equations—but with increasing driving force it gains more degrees of freedom and eventually becomes turbulent. 2 , 3 The RB paradigm applies to heat transfer as well as mass transfer if it is driven by density differences—for example, in a system with heavier salty water at the top and lighter fresh water at the bottom, as can be found in the ocean and in industrial applications.
Several reasons account for the paradigm’s popularity. The underlying dynamical equations—the Navier–Stokes equation, the advection–diffusion equation, and the continuity equation—result from momentum, energy, and mass conservation, respectively. And the respective boundary conditions are well known, so the system is mathematically well defined. The RB system is closed, so that exact global balances between the forcing and the dissipation can be derived. It also has various symmetries, such as temporal and spatial translation symmetries, rotational symmetry, and, for small-enough temperature differences, top–bottom reflection symmetry; they make it attractive for theoretical approaches. And thanks to its simple geometry, the system is accessible to controlled experiments and to direct numerical simulations, provided the thermal driving is not too strong.
Dimensionless numbers
The most relevant question in turbulent RB convection is, How does the heat transport—that is, the time- and area-averaged vertical heat flux (in dimensionless form, the Nusselt number
For a Rayleigh–Bénard (RB) cell of height
In principle, there are three methods for achieving large Rayleigh numbers in an RB system: Maintain a large
Here are some typical values for the Rayleigh and Prandtl numbers: Convective fluid motion sets in at
In the atmosphere, where
The box above lists some typical values for
Classical regime
In the regime of Rayleigh numbers up to
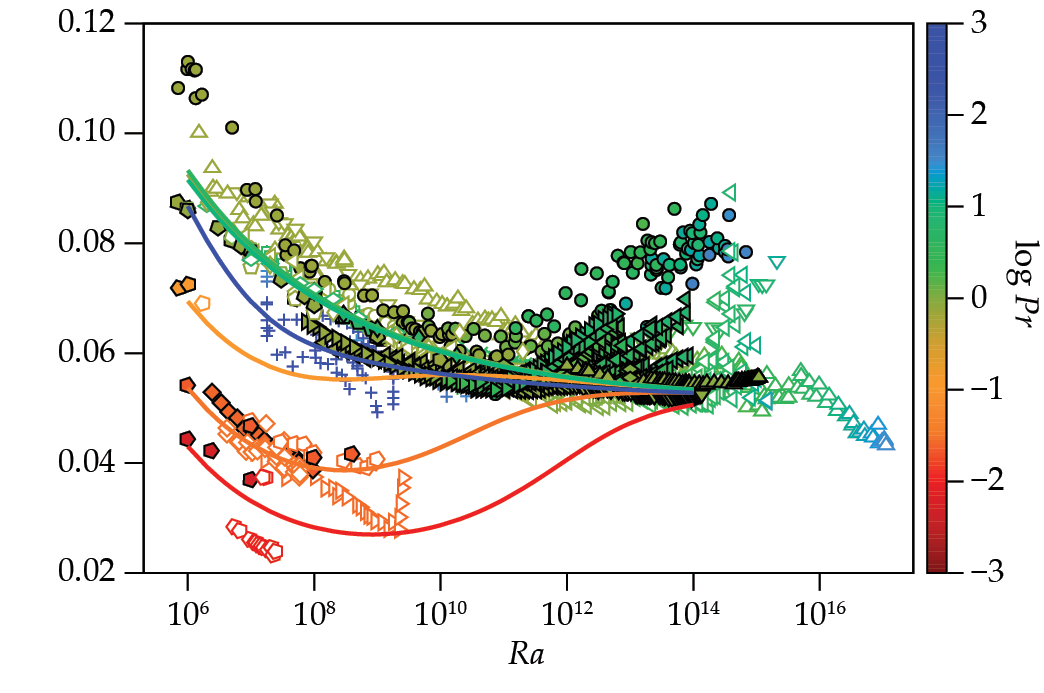
Figure 2.

Heat transport, parameterized by the dimensionless Nusselt number
The unifying theory uses two exact equations, which are straightforwardly obtained by volume integration and the divergence theorem from the Navier–Stokes equations for the velocity field
Those equations are remarkable insofar as they connect volume-averaged quantities (
Figure 3.

The analogy between Rayleigh–Bénard flow and parallel flow along a flat plate. (a–c) In turbulent Rayleigh–Bénard convection, the core part of the flow is always turbulent (Kolmogorov turbulence), whereas the flow velocity along the wall drops to zero, as illustrated by the decreasing magnitude of blue arrows on each side in panel a. With increasing thermal driving strength—in other words, increasing Rayleigh number

Because of the differing physics in the bulk and in the boundary layers, their scaling behaviors differ as well. That, in turn, rules out the traditionally assumed pure scaling behavior
How do the four individual contributions in equations
The splitting of wall-bounded turbulent flow into two regions in equations
The details of the GL theory are worked out in references and . The theory describes the experimentally and numerically observed dependencies
The key idea of the GL theory—namely, to start from exact global balance equations and to split the dissipation rates into boundary-layer and bulk contributions—is quite general. It has also been applied successfully to various other turbulent flows, such as internally heated turbulence, double-diffusive convection—in which the flow velocity is coupled to both the temperature and the salinity—horizontal convection, and magnetohydrodynamically driven turbulence.
Experiments at large
For very large thermal driving beyond
To open the large-
In later work, Roche and his colleagues found the transition Rayleigh number to vary up to
Russell Donnelly and coworkers at the University of Oregon followed Libchaber’s path of using helium gas as the working fluid close to its critical point,
8
but they increased the height of the RB cell and achieved an even larger
Guenter Ahlers and Eberhard Bodenschatz proposed another idea for how to achieve very large
The discrepancy in the large-
Ultimate turbulence regime
What do theories suggest about the existence of an ultimate regime? As early as 1962, Robert Kraichnan proposed an ultimate regime of RB convection
12
and assumed a fully turbulent boundary layer and a certain scaling relation between
The GL theory of thermal convection
4
also suggests an ultimate regime: For large-enough driving strength, the laminar Prandtl–Blasius boundary layers, shown in figure
Typically, such an onset of shear instability in wall-parallel flow happens when the shear Reynolds number
What dependence
How then can one reconcile the various seemingly contradictory measurements of
The subcritical nature of the transition implies that multiple states can coexist and that the transition is hysteretic—it depends on the system’s history—and that for strong-enough shear, even quite small disturbances can trigger the transition from laminar flow to turbulent flow (notice the analogy between figure
Although the transition toward an ultimate turbulence regime for RB turbulence is under intense discussion, no one disputes its relevance for Taylor–Couette (TC) turbulence. 17 The TC system—two coaxial corotating or counterrotating cylinders with fluid between them—is sometimes called the twin of the RB configuration because of many similarities between the two systems. 18 The analogy between RB and TC also holds in the ultimate regime and has been observed in all of the experiments and numerical simulations of turbulent TC flow made at large-enough driving strength.
That large-enough driving strength is more easily accessible in TC flow than in RB flow reflects the fact that the mechanical driving in TC flow is much more effective than the thermal driving in RB flow. Similarly, one should also expect an ultimate regime in pipe flow, horizontal convection, and other systems. Were the existence of an ultimate regime doubted in any of those flows, then one would have to come up with a mechanism by which the laminar flow in the boundary layers would remain laminar at arbitrarily large driving strength and the transition to turbulence would be suppressed. Frankly, we do not see what such a mechanism could be.
How then can the controversy on the ultimate regime in RB flow be settled? Given that striving toward ever-larger experiments and numerical simulations is extremely difficult and costly, one possibly promising route is to further explore the analogy to the laminar-to-turbulent transition in flow around a plate, illustrated in figure
The issue is of utmost relevance: Researchers must understand how to extrapolate the heat flux from controlled lab-scale experiments to the scales relevant in geophysical contexts. Whether a transition to an ultimate regime occurs or not will change the heat flux by orders of magnitude. But climate models and models for heat circulation in the ocean—with their implications for melting glaciers, nutrition transport, and the prediction of tipping points—clearly require more precision and reliability.
The scientific insights conveyed in this article come from more than three decades of collaborations and interactions with colleagues, postdocs, and doctoral students. We thank all of them for their contributions and for the intellectual pleasure we have enjoyed while working together. We thank Dennis van Gils for help with the figures.
References
1. E. Bodenschatz, W. Pesch, G. Ahlers, Annu. Rev. Fluid Mech. 32, 709 (2000). https://doi.org/10.1146/annurev.fluid.32.1.709
2. G. Ahlers, S. Grossmann, D. Lohse, Rev. Mod. Phys. 81, 503 (2009). https://doi.org/10.1103/RevModPhys.81.503
3. D. Lohse, K.-Q. Xia, Annu. Rev. Fluid Mech. 42, 335 (2010); https://doi.org/10.1146/annurev.fluid.010908.165152
F. Chillà, J. Schumacher, Eur. Phys. J. E 35, 58 (2012); https://doi.org/10.1140/epje/i2012-12058-1
K.-Q. Xia, Theor. Appl. Mech. Lett. 3, 052001 (2013); https://doi.org/10.1063/2.1305201
O. Shishkina, Phys. Rev. Fluids 6, 090502 (2021). https://doi.org/10.1103/PhysRevFluids.6.0905024. S. Grossmann, D. Lohse, J. Fluid Mech. 407, 27 (2000); https://doi.org/10.1017/S0022112099007545
S. Grossmann, D. Lohse, Phys. Rev. Lett. 86, 3316 (2001); https://doi.org/10.1103/PhysRevLett.86.3316
R. J. A. M. Stevens et al., J. Fluid Mech. 730, 295 (2013). https://doi.org/10.1017/jfm.2013.2985. B. Castaing et al., J. Fluid Mech. 204, 1 (1989). https://doi.org/10.1017/S0022112089001643
6. X. Chavanne et al., Phys. Rev. Lett. 79, 3648 (1997). https://doi.org/10.1103/PhysRevLett.79.3648
7. P.-E. Roche, New J. Phys. 22, 073056 (2020); https://doi.org/10.1088/1367-2630/ab9449
P.-E. Roche et al., New J. Phys. 12, 085014 (2010). https://doi.org/10.1088/1367-2630/12/8/0850148. J. J. Niemela et al., Nature 404, 837 (2000). https://doi.org/10.1038/35009036
9. J. J. Niemela, K. R. Sreenivasan, J. Fluid Mech. 481, 355 (2003). https://doi.org/10.1017/S0022112003004087
10. P. Urban et al., New J. Phys. 16, 053042 (2014). https://doi.org/10.1088/1367-2630/16/5/053042
11. G. Ahlers et al., New J. Phys. 14, 103012 (2012); https://doi.org/10.1088/1367-2630/14/10/103012
X. He et al., Phys. Rev. Lett. 108, 024502 (2012). https://doi.org/10.1103/PhysRevLett.108.02450212. R. H. Kraichnan, Phys. Fluids 5, 1374 (1962). https://doi.org/10.1063/1.1706533
13. L. N. Howard, J. Fluid Mech. 17, 405 (1963). https://doi.org/10.1017/S0022112063001427
14. F. H. Busse, Rep. Prog. Phys. 41, 1929 (1978); https://doi.org/10.1088/0034-4885/41/12/003
C. R. Doering, P. Constantin, Phys. Rev. E 53, 5957 (1996). https://doi.org/10.1103/PhysRevE.53.595715. P. Manneville, Mech. Eng. Rev. 3, 15-00684 (2016); https://doi.org/10.1299/mer.15-00684
M. Avila, D. Barkley, B. Hof, Annu. Rev. Fluid Mech. 55, 575 (2023). https://doi.org/10.1146/annurev-fluid-120720-02595716. S. Grossmann, D. Lohse, Phys. Fluids 23, 045108 (2011). https://doi.org/10.1063/1.3582362
17. S. Grossmann, D. Lohse, C. Sun, Annu. Rev. Fluid Mech. 48, 53 (2016). https://doi.org/10.1146/annurev-fluid-122414-034353
18. F. H. Busse, Physics 5, 4 (2012). https://doi.org/10.1103/Physics.5.4
More about the authors
Detlef Lohse (d.lohse@utwente.nl) is the chair of the physics of fluids group at the University of Twente in Enschede, the Netherlands. Olga Shishkina (olga.shishkina@ds.mpg.de) is group leader at the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany.






