The interdisciplinary journey to fractal bionics

In the science fiction world of my childhood, damaged body parts were replaced by artificial implants that restored or even enhanced performance. I never tired of watching how the protagonists of 1970s TV shows like The Six Million Dollar Man and The Bionic Woman used their superior artificial eyes and ears to outwit villains.

Fifty years on, that science fiction is transforming into science fact. Electronic devices have been implanted into eyes with the aim of restoring vision to patients with degenerative retinal diseases. Those diseases strike 1 in 10 people over age 50 and have no conventional cure. More than 160 000 brain implant surgeries have targeted neurological disorders such as Parkinson’s disease. And people with amputated limbs can now receive interactive prosthetic implants that restore some mobility. Research continues to bring the capabilities of implants closer to those of my bionic heroes.

My journey into bionics began a decade ago when I was invited to the Pufendorf Institute for Advanced Studies. Located at Lund University in Sweden, the institute assembles eclectic teams to address diverse research themes. I was excited that my theme for the visit focused on vision because it united my backgrounds in physics and art. It also allowed me to listen to perspectives from those in other disciplines. My interests quickly gravitated to designing artificial neurons for the retina, inspired by the fractal geometry of the biological ones.

Brainstorming sessions with Lund ophthalmologist Maria Thereza Perez highlighted the medical challenge of fixing the retina’s electrical wiring when it stops working. Perez described how electrodes were being used to stimulate electrical signals in neurons that no longer received messages from their damaged neighbors. The idea was far from novel, she said. More than two centuries earlier, Charles Le Roy had applied electricity to a patient’s eyes, causing him to see flashes of light. Luigi Galvani had done the same to frog muscles, causing them to twitch. But those researchers knew little about the body’s wiring. The concept of neurons arrived over a century later.

Now, it’s known that electricity passes across synapses from neuron to neuron much like electricity flows between resistors in an electric circuit. And similarly to a faulty resistor, a damaged neuron will disrupt transmission through the circuit. To fix the circuit, today’s surgeons can implant miniature electrodes into the body rather than relying on the crude external wires used by Le Roy and Galvani.

As I listened to Perez, I sensed the remarkable opportunity for interdisciplinary collaboration: Physicists could bring their knowledge of electrical networks; chemists, their knowledge of the materials needed to build the electrodes; and neuroscientists, their knowledge of the body’s interactions.

Such a collaboration could potentially create artificial neurons that integrate seamlessly with their natural counterparts to form a hybrid system, just like the science fiction heroes of the 1970s took inspiration from biology and embraced bionics.

The fractal nature of neurons

Human neurons vary in length from microns up to a meter. They form immense networks—humans have as many connections between neurons in a single cubic centimeter of their brain as there are stars in the Milky Way. Maintaining the health of those connections is important for daily tasks. In addition to brain connections facilitating thought, humans rely on neurons to connect to their eyes for sight and to their limbs for movement. The neurons’ complex patterns contrast sharply with the simpler wiring of cell phones and computers.

Fractal branches are prevalent in nature. Bronchial trees and blood vessels in human bodies benefit from those structures. The branches and their gaps form two fractals sharing a huge interface that balances their operational performance with associated costs. Neurons exploit the fractal geometry of their branches and gaps to establish connections to their neighbors. The inset of figure 1 shows multiple views of a bipolar neuron that provides crucial connections between the eye’s photoreceptors and other retinal neurons that carry signals to the brain. The neuron’s branching dendrites are fractal; they generate repeating patterns at different size scales as they grow out from its center.

Figure 1.

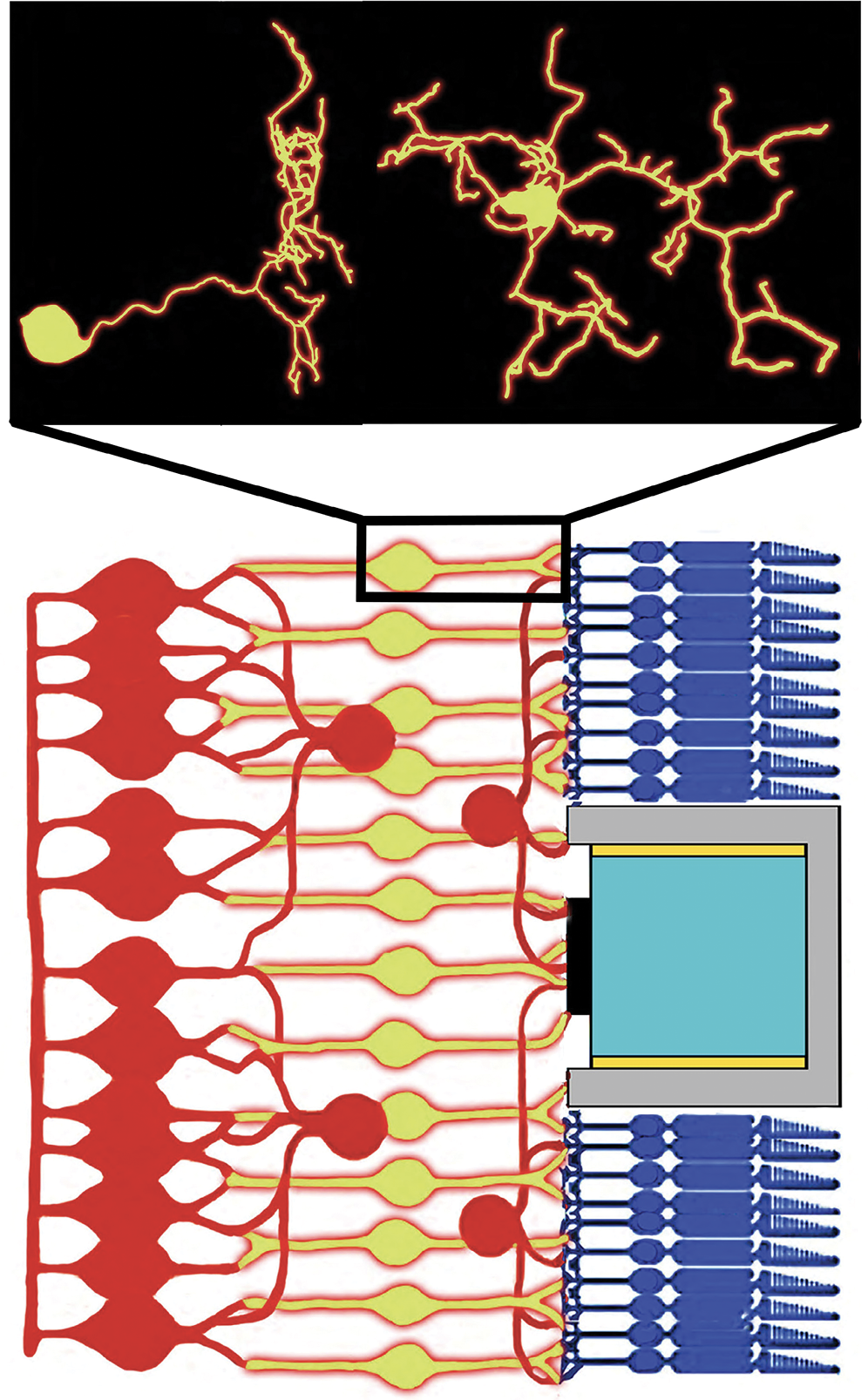
An impressive piece in the story of nature’s fractals is that only a few pattern repetitions are required to achieve that performance–cost balancing act. For some of nature’s fractals, patterns typically repeat over a magnification factor of only 25. That is good news for bioengineers who want to replicate their geometry: Bioinspired electrodes will be less challenging to fabricate if their branches span a limited range of sizes.

Fractals fall into two families: exact and statistical. Mathematicians assemble exact fractals by repeating patterns precisely. Nature’s randomness disrupts the precision, and only the pattern’s statistical qualities repeat. Consequently, statistical fractals exhibited in systems such as neurons only appear similar at different scales.

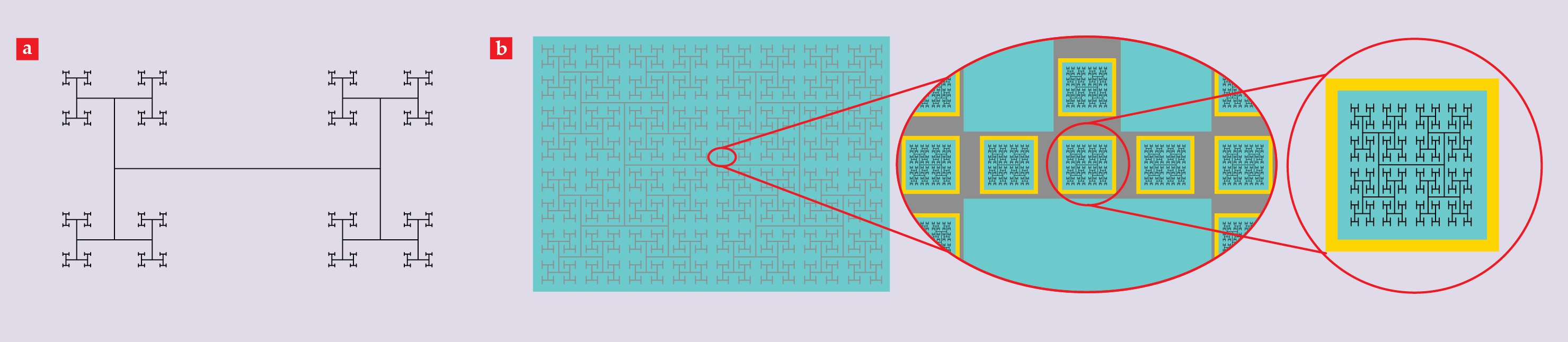
The H-tree pattern shown in figure 2a is an example of simpler exact electrodes. Most discussions of fractals quickly gravitate to the concept of the fractal dimension D. At each level of repetition, the number of branches N is proportional to L^−D, where L is the branch length. That power law generates the pattern’s scale invariance, and its exponent D sets the rate of shrinkage of L between the levels. Higher D values correspond to slower rates. Consequently, D measures the relative contributions of coarse and fine structure in the fractal mix; fine structure plays an increasing role as D rises. Nature’s fractals maximize their functional properties by tuning their D values, and our electrodes do the same.

Figure 2.

Heading into the retina

Figure 2b shows a design for using H-tree electrodes to collect charge from an array of photodiodes. One large H-tree electrode is deposited on a photodiode layer. That large electrode features an array of holes in its branches. Within each hole, an insulating interface separates the large electrode from the photodiode sides. A smaller H-tree electrode also nests in each hole. When the photodiode is illuminated, its charge migrates up to the surface to be collected by the smaller H-tree electrode. That active electrode then generates an electric field with the larger, grounded electrode.

Figure 1 demonstrates how the design might work in practice by showing a subretinal implant, which is a photodiode replacing a diseased photoreceptor. That strategy is feasible because common diseases predominantly attack the photoreceptors but leave the neighboring neurons sufficiently intact to interface with the photodiode’s electrodes. In principle, the size of each of the active electrodes would match the photoreceptor diameter (about 5 µm), and the ground electrode would span the diseased region.

The subretinal implant celebrates the basic philosophy of bionics—that the hybrid system should maximize natural functionality. Signals from the subretinal implant pass through the retina’s circuitry on the way to the optic nerve and in principle benefit from the image compression and processing functions performed by the millions of retinal neurons. Those functions are important for seeing. Even with the retina working, a billion signals pass down the optic nerve each second, requiring the brain to dedicate up to 30% of its volume to processing the incoming data. Without its retinal outpost, the brain’s operation becomes strained.

To stimulate the targeted bipolar neurons, the electrical field generated by the electrodes changes the potential difference across ion channels that permeate the neuron’s surface membrane. The induced ion flow through those channels triggers signals along the neuron’s branches. Those signals then pass to neighboring neurons via synaptic connections on the neuron’s surface.

Our team’s electrical simulations of the photodiode–neuron operation highlight the advantage of adopting fractal designs: Significant amounts of charge reside on the H-tree sidewalls. Compared with Euclidean electrode designs, such as grids and squares, the large sidewall surfaces associated with the fractal’s long boundaries generate enhanced capacitances and therefore larger stimulating fields. Our simulations show that the result is game changing: The fractal electrode stimulates all neighboring neurons, whereas the equivalent square electrode stimulates less than 10%. Along with translating to higher-resolution vision for retinal implants, the fractal advantage could also apply to brain and prosthetic limb implants.

Fractal herding at the biophilic interface

Teaching my favorite course—Physics of Light, Color, and Vision—reminds me that implants are only as strong as their weakest link. Students often pull out their cell phones and, trying to be helpful, suggest that I should insert a phone camera into the eye. Indeed, there are high-end cameras that exceed the eye’s pixel densities. Camera technology, however, isn’t designed to interface with living systems. If an implant is rejected by the eye’s cells, then its electrical performance becomes irrelevant. In particular, the superior fractal capacitances won’t have a chance to shine.

Neuron biocompatibility, meaning its tolerance of a foreign implant, is therefore the driving force of any design. The design principles can be thought of as a three-legged stool. The two legs that have received the most attention are the chemical environment and physical texture provided by the electrode’s materials. The third leg is the electrode’s shape. Ultimately, bionics should be biophilic: Neurons should be attracted to, rather than simply tolerant of, the electrode. Fractal shapes could provide the key to that attraction.

Although bioengineers typically focus on neurons, glial cells also deserve their place in the research spotlight. Serving as the neurons’ life-support system, glial cells provide the trophic and metabolic support for neurons to maintain their health and transmit their signals. To deliver the desired biophilic properties to our electrodes, we exploit the different reactions that neurons and glial cells have to artificial surfaces.

Figure 3 shows an electrode immersed in an in vitro culture of neurons and glia. We grow carbon nanotubes patterned into an H tree on a silicon dioxide substrate. When the nanotubes grow vertically from the substrate (out of the page in figure 3), they tangle into a conducting forest with a textured canopy. Neurons accumulate on the textured nanotube branches because they adhere strongly to surface textures that resemble the retina’s multiscaled structural environment. In contrast, the glial cells proliferate in the gaps because the smoother SiO₂ surfaces encourage their division and growth. Once herded into the gaps, the glia can’t physically hinder the neuron–electrode interactions but are still sufficiently close to provide their vital health support.

Figure 3.

Herding increases with the amount of time for cell growth, and fractals outpace Euclidean electrodes significantly in the race. In particular, H trees with high D support vast colonies of glia because their multiscaled gaps provide the optimal balance between the glial cells’ chemical need to be close to the neurons and their physical need to have open spaces in which to divide and grow. The neuron-rich branches also thrive because their long fractal boundaries with the gaps boost the health benefits of the glial colonies.

Those thriving neurons then optimize their network. Following an initial dendritic growth spurt to establish connections, the neurons collect into bigger clusters and prune some of those connections. Structurally, the optimization resembles small-world networks—efficient systems that link all locations using relatively few connections. You may have experienced small-world networks through the hub system used by airlines. There’s no guarantee of a direct flight between any two airports, but you can get where you need to go by flying through major hubs. Fortunately, nature’s neurons provide better service.

Fractal resonance

Having herded neurons onto the electrodes, our collaboration proposed that fractal resonance would further help them thrive. Our hypothesis was that matching the electrodes to the neurons’ precise fractal characteristics would induce greater connectivity between the two. Although the H tree shares the multiscale character of nature’s fractals, the exact repetition of its straight lines and 90° turns are far from bioinspired.

By analyzing examples of neurons from both the retina (bipolar neurons) and the brain (hippocampal neurons), we found that the way their dendrites weave through space is crucial for generating their statistical fractal patterns. The neurons’ attraction to that fractal weaving behavior raised a fundamental question: What are the negative consequences of deviating from the natural fractal form? If neuron functionality deteriorates, then fractal resonance should drive all electrode designs.

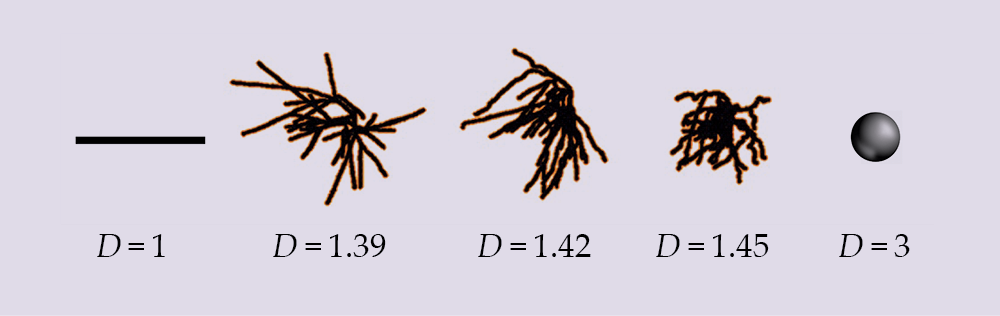
To deliver the answers, we created neurons that nature chose not to by imaging neurons using confocal microscopy and then mathematically distorting their dendrite weaving angles. In figure 4, the middle neuron is natural, and the left and right neurons are distortions created by straightening and curling the dendrites. The distortions cause the neurons’ D values to deviate from the natural value of 1.42 in opposite directions. Continuing the curling process would ultimately produce a 3D sphere, with the increased fine structure filling that volume. In contrast, completely straightening the branches and lining them up end to end would produce a smooth, 1D line, devoid of fine structure.

Figure 4.

Ramping up D increases a neuron’s ability to communicate with its neighbors because of a rise in connectivity density. That quantifies the neuron’s physical profile within a given volume and so measures the increased exposure of synapses on the dendrites’ surfaces. Yet neurons need to balance increases in connectivity density with the costs of constructing and maintaining those connections. Construction costs include the amount of dendritic mass within a given volume. Maintenance costs include the energy to operate the ion channels, which increases with the dendritic surface area within a given volume.

Crucially, connectivity and its costs increase at different rates as D rises, and that allows the neurons to balance those competing factors. That balance can be quantified using balanced connectivity, which considers the ratio of the connectivity rate and cost rate. As expected, natural neurons have D values that cluster around the peak in the balanced connectivity curve; nature found the optimal amount of fine structure.

The distorted neurons have D values that lie away from the peak, and the drop-off in balanced connectivity quantifies the deterioration associated with deviating from the neuron’s natural form. The Euclidean shapes also lie well away from the optimal balance, demonstrating why neurons follow fractal rather than Euclidean geometries. The lack of gaps in the sphere generates a large profile, but the heavy price paid for its large mass density explains why neurons aren’t that shape. Simple, straight lines use little mass at a given location, but they pay the price of spreading their profile over expansive regions.

If the electrode’s D value is matched to that of the neurons, the neurons can preserve their natural weave during the adhesion process. They will then benefit from being at the peak in their balanced connectivity when interacting with their neighboring neurons and the electrode. In contrast, requiring neurons to grow along the straight lines and turn the tight corners of Euclidean electrodes, such as grids, will force neurons down the slope of the balanced connectivity curve.

Fractal resonance can be compared to an aircraft on final approach. Whereas pilots prefer to fly straight when approaching 1D, straight runways, neurons like to maintain their weave as they land on our electrodes. Ultimately, different neuron types might be guided to different electrode runways depending on their D values. Using the equivalent of autopilot, we are developing software to predict the electrode shape that provides large overlaps with the dendrites while minimizing their distortion. Those statistical fractal electrodes will be constructed using 3D printers for future clinical trials.

The brave new world of fractal bionics

How far do the fractal advantages get us? The pioneering implants used to replace damaged photoreceptors have 4% of typical visual acuity. That’s worse than the legal blindness level of 10%, below which tasks like driving safely are impossible. The square electrodes in those original subretinal implant experiments had a low capacitance. They didn’t generate large stimulating fields, and the few neurons that adhered to their surfaces were likely distorted, which prevented them from effectively passing signals to their retinal neighbors.

In contrast, our simulated fractal implants are expected to have roughly 25% acuity. We created 20 µm photodiodes, which we made larger than photoreceptors to accommodate for their poorer performance, and the resulting vision is accurate enough to perform many daily tasks. Figure 5 compares those two acuity levels against natural vision using photos of my old friend Griffon that progressively reduce in pixel density.

Figure 5.

I recently returned to the Pufendorf Institute and reminisced with Perez about our bionic adventure. We agreed to relabel our artificial neurons as “interconnects” to capture their multiple functions that go beyond the electrical performance suggested by calling them “electrodes.” For example, the multiscaled branching properties that allow trees to sway in the wind without breaking can translate to mechanically flexible electronics—the interconnects could conform to the retina’s shape, and surgeons might even curl them up for delivery through less obtrusive insertions. Advances that use fractal shapes to manipulate light on the nanometer scale might even allow wavelength tuning for color vision.

Building on the solid-state chip revolution, electronic strategies continue to be an obvious approach to retinal repair. Although my research focuses on interconnects, other advances—such as improved photodiodes or supplemental implantable batteries—could come from the implant’s power source. Alternative long-term strategies focus on fabricating organic artificial photoreceptors or growing new biological systems using stem cells. Regardless of the approach, future advances will require collaboration between bioengineers and neuroscientists to foster a greater understanding of the interactions between the natural and introduced systems. The interdisciplinary endeavors undertaken already emphasize how far the field has come since Le Roy and Galvani’s pioneering experiments.