Dipolar supersolids: Solid and superfluid at the same time

The microscopic laws of quantum mechanics can influence behavior at the macroscopic scale. In superconductors, for example, the coupling of electrons into Cooper pairs leads to current flow without resistance. In superfluids, the collective motion of atoms as a coherent matter wave suppresses dissipation and produces frictionless mass flow. Both phenomena starkly contrast with our everyday experience. Recent experiments with ultracold gases of magnetic atoms have demonstrated that a long sought after and, perhaps, even more counterintuitive “super” state exists: the supersolid, a state that combines the properties of a solid and a superfluid.

One of the fundamental principles of quantum mechanics is the superposition principle. A single atom can be not only in a particular quantum state, such as spin up or down, but also in a coherent superposition of two such states.

Since the 1950s theoretical physicists have pondered whether quantum mechanics allows for a phase of matter—that is, a collective state of many atoms—that shows behavior similar to superposition. ¹ That so-called supersolid phase would simultaneously feature the contradictory properties of a superfluid’s perfect flow and of a solid’s rigid, crystalline structure. Think of a jar of honey, whose contents can be in a liquid or in a crystalline phase. A hypothetical supersolid honey would, counterintuitively, exhibit a quantum mechanical superposition of both phases.

The idea of supersolids triggered an ongoing decade-long search for that exotic state in helium, which was for a long time considered the most “quantum” material available. Liquid ⁴He famously becomes a superfluid at temperatures below about 2.17 K at atmospheric pressure. Its superfluid behavior is closely related to Bose–Einstein condensation, a phenomenon in which atoms accumulate in the lowest quantum mechanical energy state of a system and form a collective matter wave. Unlike the energy-dissipating random motion of particles in a classical liquid, a superfluid’s coherent flow is frictionless.

Not only can helium be a liquid or a superfluid, but at sufficiently high pressures of several megapascals and temperatures around a few kelvin, it also can form a solid. In that solid, the helium atoms arrange in the rigid periodic structure of a crystal lattice. Intuitively, solid helium thus shouldn’t have superfluid properties. But theoretical studies have long suggested that solid helium may turn into a supersolid if the lattice contains empty sites, so-called vacancies, in the crystal structure that can easily hop around and become delocalized over the entire crystal. At sufficiently low temperatures, those vacancies can undergo Bose–Einstein condensation just like atoms, and superfluid properties emerge. While most of the helium remains a solid, a small part of the solid’s mass becomes free to flow without friction.

Supersolid formation should be clear from measurements of transport properties or of the moment of inertia of a bulk helium sample. Such measurements turned out to be very challenging, and the results often difficult to interpret. (See Physics Today, February 2008, page 14 , and the article by Robert Hallock, Physics Today, May 2015, page 30 .) For example, theory predicts that some defects are necessary for supersolidity, but in experiments, too many or the wrong sorts of impurities can change the properties beyond what’s modeled. Moreover, changes in the moment of inertia that seemingly indicate the presence of a supersolid can instead result from unexpected changes in the sheer modulus of a helium crystal at low temperatures. So far, the consensus is that no conclusive evidence exists for supersolidity in bulk ⁴He. It seems to be either a solid or a superfluid, but just like honey, it can’t be in a superposition of both.

Can a superfluid be solid?

Over the past two decades, ultracold atomic gases have emerged as a new kind of quantum material for exploring unusual phases of matter. (See Physics Today, August 2017, page 17 , and the article by Keith Burnett, Mark Edwards, and Charles Clark, Physics Today, December 1999, page 37 .) Those gases are collections of atoms cooled to near absolute zero in two stages. First, through laser cooling, the atoms are slowed down by the recoil from thousands of precisely tuned photon absorption and emission cycles. Then evaporation provides further cooling, reminiscent of a cooling cup of hot coffee, where the most energetic coffee particles evaporate away as steam. Similarly, in ultracold gases, the most energetic atoms can continuously be removed, and the remaining atoms rethermalize at lower and lower temperatures.

In contrast to familiar materials, ultracold gases contain only between a few thousand and a few million atoms. They must also be isolated from their environment in traps formed by focused laser beams or magnetic fields in ultrahigh-vacuum chambers. As their preparation is specific to a certain atomic species, however, they are inherently clean and controllable. Crucially, they can be manipulated and minutely probed with the precise tools of atomic physics to create textbook realizations of open quantum mechanical questions.

Once cooled to sufficiently low temperatures—typically a few tens of nanokelvin—atomic gases will undergo Bose–Einstein condensation. The resulting quantum material is about a million times as dilute as helium but still shows similar superfluid properties. That low density means individual atoms are fairly isolated from one another and, as a result, typically much easier to model and understand than helium. Atomic gases’ superfluidity allows supersolidity to be considered from a new direction: Instead of a solid turning into a supersolid, can a gaseous superfluid turn into a supersolid?

For a supersolid to form, the atoms in the Bose–Einstein condensate (BEC) must spontaneously arrange into a periodic crystal structure while maintaining their collective superfluid properties. That spatial periodicity has an associated characteristic length scale, which must arise in some way during the transition to a supersolid. The most straightforward way to introduce that length scale is to manipulate the BEC with laser beams, whose wavelengths naturally offer a length scale.

The specific implementations vary. For example, some researchers place the atoms in a standing wave of an optical cavity, and others use lasers to induce a spin–orbit coupling. ² The result in both cases is the spontaneous emergence of a periodic crystal structure and properties of a supersolid, such as characteristic excitations and coherence. But the corresponding crystals have an infinitely stiff structure fixed by the external laser field. The atoms are thus always localized at the same distance from one another and only behave in that way because of an external influence. Both properties are fundamentally distinct from those of natural materials, whose atoms are free to oscillate around the individual lattice sites and spontaneously arrange into crystal patterns because of their intrinsic interactions.

Ultracold dipolar atoms

Properties more akin to those of real materials are possible with a BEC made from highly magnetic atoms. In most BECs, ultracold atoms interact only through contact interactions—they repel each other isotropically like billiard balls when a pair of them get close. The atoms in magnetic BECs also feature long-range dipolar interactions, similar to those of bar magnets. Depending on the relative orientation of the atoms, the interactions can be attractive or repulsive. Suitable atomic species that exhibit sizable dipolar interactions include transition metals, such as chromium, and lanthanides, such as dysprosium and erbium. Because of their complex electronic structure, those elements feature large angular momenta, which produce large magnetic dipole moments.

The competition between contact and dipolar interactions produces behavior that can be understood best from their excitation spectrum, shown in figure 1. The excitations in a normal BEC, with only contact interactions, are simple sound waves (the energy spectrum shown in blue), but a magnetic BEC can additionally support so-called rotons. ³

Figure 1.

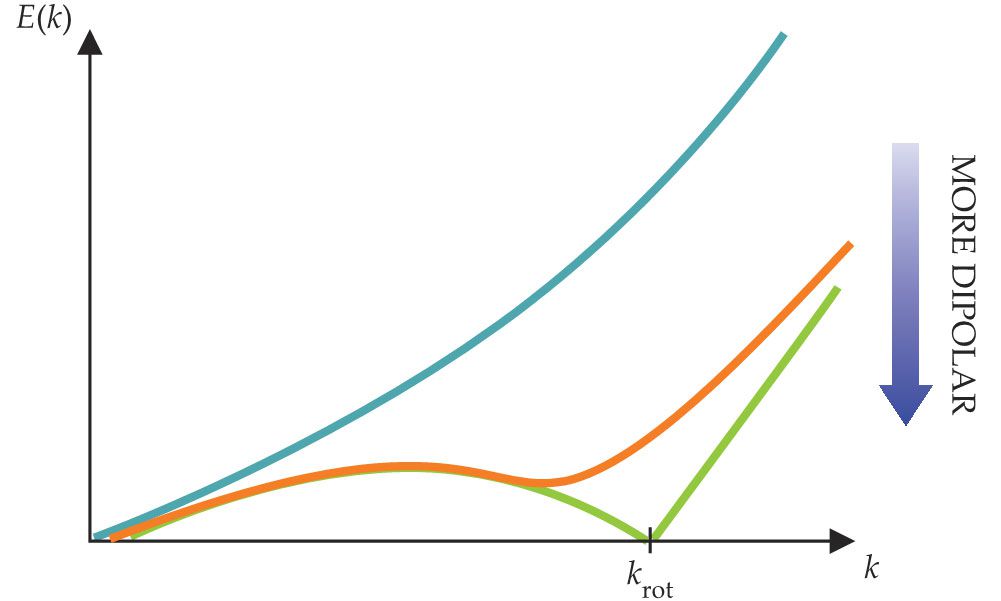
Rotons are excitations with a finite momentum (k_rot in figure 1) that cost less energy to excite as dipolar interactions strengthen, as shown by the green curve’s lower local energy minimum than the orange curve’s in figure 1. They are most intuitively pictured in a BEC confined to a tubelike potential, in which a roton is a small sinusoidal modulation on top of the smooth BEC wavefunction. The length scale of that modulation is related to the inverse of the roton’s momentum. The less energy needed to excite the modulation, the higher the number of participating atoms, until at some point, the modulation is no longer small but a significant crystal structure. Given the right conditions, magnetic BECs thus favor crystal structures, which form solely because of the interactions among the atoms.

Classical ferrofluids—nanoscale ferromagnetic particles suspended in an oily solution—show analogous restructuring behavior. When those ferrofluids are on a hydrophobic surface and polarized by a sufficiently large external magnetic field, they can undergo a so-called Rosensweig instability to form a crystal of little droplets, shown in figure 2. The mechanism of that instability is similar to the one responsible for crystallization in dipolar BECs; both systems feature a dispersion relation with a minimum at finite momentum. The key difference, however, is that dipolar BECs are quantum systems with the possibility of coherent, superfluid behavior.

Figure 2.

But there’s a catch: For ultracold atomic gases to be stable, the sum of all interactions between the atoms must be repulsive. (See Physics Today, August 2000, page 17 .) Without that repulsion, the atoms move closer and closer together and eventually form molecules or react in other ways. For example, if three atoms come close enough to one another to collide inelastically, two of them can form a molecule, with the third carrying away excess energy. Typically, neither the molecule nor the remaining atom can be trapped, so the process leads to strong losses and eventually the destruction of the sample.

The conditions for stability appear to be in conflict with the dominant dipolar interactions necessary for crystallization. As in a classical ferrofluid, the sites of the BEC crystal are droplets made up of many atoms, rather than individual atoms, as is the case in helium and other solids. The structure is sometimes referred to as a droplet crystal. Inside the elongated droplets, the atoms predominantly arrange themselves in a head-to-tail configuration, in which dipolar interactions are strongly attractive. Stability would then require strong repulsive contact interactions to compensate for the dipolar interactions, but stronger contact interactions would preclude crystallization of the BEC in the first place. Either the atoms form a stable BEC or an unstable crystal. The result is that dipolar BECs collapse when they approach the expected crystallization transition, ⁴ as was observed for weakly dipolar chromium atoms in 2008.

Dysprosium BECs

The unexpected solution to the apparent conflict between stability and crystallization turned out to be BECs made of more magnetic atoms. In 2016, experiments similar to the earlier studies on chromium found that BECs of dysprosium atoms, which feature a magnetic dipole moment that is almost twice as large as chromium’s, did spontaneously self-assemble into droplet crystals. ⁵ That observation was a big surprise, and making sense of it required an extension of the established theoretical models of dipolar BECs.

The key to understanding that stability against collapse is a phenomenon known as quantum fluctuations. The wavefunction of a BEC can be modulated by not only rotons but also many other excitations with different energies and momenta given by the dispersion relation shown in figure 1. As quantum objects, those excitations will always fluctuate with some amplitude even at their lowest energies. So small but persistent noise—the quantum fluctuations—will always be present on top of the smooth BEC wavefunction. Counterintuitively, that tiny effect can stabilize gases such that they can form stable droplets. ⁶ (See the article by Igor Ferrier-Barbut, Physics Today, April 2019, page 46 .)

The quantum fluctuations of a BEC, described by Lee-Huang-Yang (LHY) corrections, have been known for decades, but they are typically negligible. Their effect, however, can become important in systems with more than one type of interaction, such as magnetic BECs, which have a combination of contact and dipolar interactions, and mixtures of different atomic species. At the point when droplet crystals would be expected to collapse, the attractive dipolar and the repulsive contact interactions almost perfectly cancel each other. What’s left is weak attractive dipolar interactions, which would normally trigger collapse but can instead be compensated for by the small repulsive LHY corrections.

The magnitude of the LHY correction scales with the number of atoms in the BEC and the magnitudes of their magnetic moments. For relatively weakly dipolar systems, such as chromium, stability requires far more atoms than the few tens of thousands that are produced experimentally—hence the system collapses. For strongly dipolar dysprosium, on the other hand, the LHY correction perfectly balances the other interactions, and stable droplet crystals can form with an experimentally accessible number of atoms, as shown in figure 2.

A supersolid, however, is more than just a crystal. The atoms forming it must also maintain the superfluid properties of the original BEC. The crystals shown in figure 2 aren’t superfluid because the individual droplets are too far apart to have overlapping wavefunctions. The BEC’s coherence, which is crucial to the superfluid nature, is thus quickly lost.

Recent experiments in the labs of Giovanni Modugno at the University of Florence in Italy, Tilman Pfau and I at the University of Stuttgart in Germany, and Francesca Ferlaino at the University of Innsbruck in Austria indicate that, in addition to crystals of isolated droplets, a small range of interaction strengths and atom numbers produces coherent crystals. ^7–9 In those crystals, the individual droplets stay mutually coherent because of their strong wavefunction overlap, which can be interpreted as a superfluid background keeping the droplets linked. The observations suggest the simultaneous presence of superfluid and crystal properties.

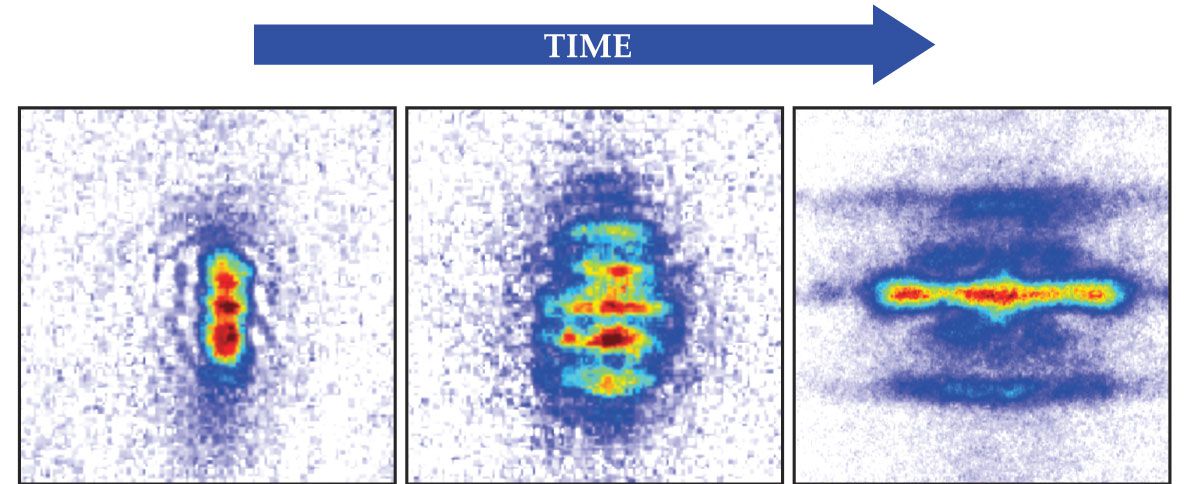
The researchers use a microscope to image the spontaneously forming crystal structure, shown in figure 3, with single-site resolution. To probe the coherence of the droplets, they turn off all trapping potentials and let the gas expand. A freed coherent matter wave produces a reproducible, high-contrast interference pattern similar to diffraction from a grating, as shown in figure 4. (A gas without coherence would instead create random or no interference patterns.) As expected, the length scale of the observed crystal structure exactly matches the roton length scale. It turns out that BECs can smoothly transform into a coherent droplet crystal simply by becoming more dipolar.

Figure 3.

Figure 4.

The magnetic moment of an atomic species is fixed, so in practice, instead of the dipolar interactions being enhanced, the gas’s contact interactions are made weaker. Such tuning of the contact interactions is possible with scattering resonances. Those resonances arise when the quantum state of two colliding atoms in a gas is energetically degenerate with a molecular bound state of the pair. Those free and bound states exhibit different Zeeman shifts, so their resonance can be controlled using an external magnetic field. In that way, the contact-interaction strength of the atoms is tunable, and the desired states—BEC, supersolid, or isolated droplet crystal—can be created at will. Although the balance of contact and dipolar interactions and their LHY corrections is subtle, the behavior is not limited to dysprosium atoms but has also been observed in gases of magnetic erbium atoms.

Coherent crystal or supersolid?

Although the observed coherence is a strong indication of superfluidity and, hence, the supersolidity of the crystal state, it’s not definitive proof. Superfluidity, Bose–Einstein condensation, and coherence are closely related but not the same thing. For example, in some low-dimensional systems, Bose–Einstein condensation is absent, but superfluidity and coherence still emerge. The superfluid properties of the system thus need to be investigated directly.

Studying how a superfluid reacts to a perturbation is a common way to assess its properties. For example, the rotation of a superfluid reveals its characteristic irrotational flow. Another perturbation well suited for the observed crystals is a sudden change of the atoms’ trapping potential or a change in the interactions in the system. In both cases the system is no longer in equilibrium and reacts by creating characteristic excitations, such as sound waves. The supersolid, which simultaneously has superfluid and solid properties, should feature two kinds of sound waves: the usual sound waves of a superfluid BEC and the sound waves from the lattice oscillations of a crystal.

Those two kinds of sound waves are closely connected to the two symmetries that are broken by the supersolid. First, similarly to a BEC, the supersolid breaks phase symmetry—upon its creation, it spontaneously acquires a certain quantum mechanical phase. Second, the emerging crystal structure breaks continuous translation symmetry. Whenever such symmetry breaking occurs, characteristic excitations, called Nambu–Goldstone modes, arise. In the case of supersolids, those modes correspond to the previously discussed sound waves. Another example from condensed-matter physics is magnons, which are excitations that emerge in ferromagnets below the Curie point when a spontaneous magnetization breaks rotational symmetry. In high-energy physics, the breaking of chiral symmetry in quantum chromodynamics is connected to the emergence of pions.

In experiments, an ultracold gas’s evolution after a sudden change of the system’s parameters indicates the presence of sound waves. ¹⁰ High-resolution images of the atomic distribution, such as those in figure 3, facilitate precise measurements of the periodic changes in the crystal spacing, the size and position of the atomic cloud, and other parameters. It is even possible to extract the characteristic mode patterns of the sound waves, in a process similar to observing the waves forming on a water surface. The observations unambiguously reveal the characteristic sound waves of both the crystal and the BEC. The coherent droplet crystals are indeed supersolids.

Not only can atomic gases transition from a superfluid to a supersolid state with the addition of a crystal structure—that is, start as a BEC with one broken symmetry and then break the second one—but they can also be cooled directly into the supersolid state and thus break two symmetries at once. That process is identical to the evaporative cooling used for BECs, except that the interaction parameters in the gas must be fine-tuned to the appropriate values for the emergence of a supersolid state prior to cooling. Moreover, dynamically changing the interactions flips the gas back and forth between the BEC and supersolid phases.

What’s next?

The experiments with dipolar gases provide clear evidence that supersolids indeed exist in nature and offer a powerful platform to explore supersolids’ properties.

Much is still unknown about the nature of that exotic state of matter. For example, several groups are currently investigating supersolid properties under rotation, in research analogous to that performed previously on helium. The fate of the transition at higher temperatures also is widely unexplored. Moreover, the crystals realized from magnetic atoms so far contain only a handful of crystal sites and are thus minuscule by the standards of a materials scientist. Making them larger is simply a matter of cooling more atoms. Boosting the laser power or cooling and manipulating the atoms more efficiently are among the many strategies—some of which are already being tested—that could increase the number of ultracold atoms. A first step in that direction is the recent extension of the one-dimensional chains of droplet crystals to a 2D triangular lattice. ¹¹

Another lingering question is the generality of the observations. Do stable droplet supersolids exist only in magnetic atoms? A change of the dipole moment by a factor of less than two from the first chromium BECs to the recent strongly dipolar dysprosium and erbium BECs turned unstable collapsing systems into supersolids. Current efforts to produce BECs of diatomic molecules could provide a new supersolid system. Those molecules can feature dipole interactions that are orders of magnitude stronger than those in magnetic atoms because of their electric dipole moments. What’s more, those interactions are tunable by external electric fields.

Other cold-atom systems in optical cavities and with spin–orbit coupling may also transition to compressible supersolids. ¹² And what about helium supersolids? Experiments are currently exploring confined superfluid ³He and ⁴He films, where transitions to structured states similar to the ones in dipolar atomic gases have been observed. ¹³

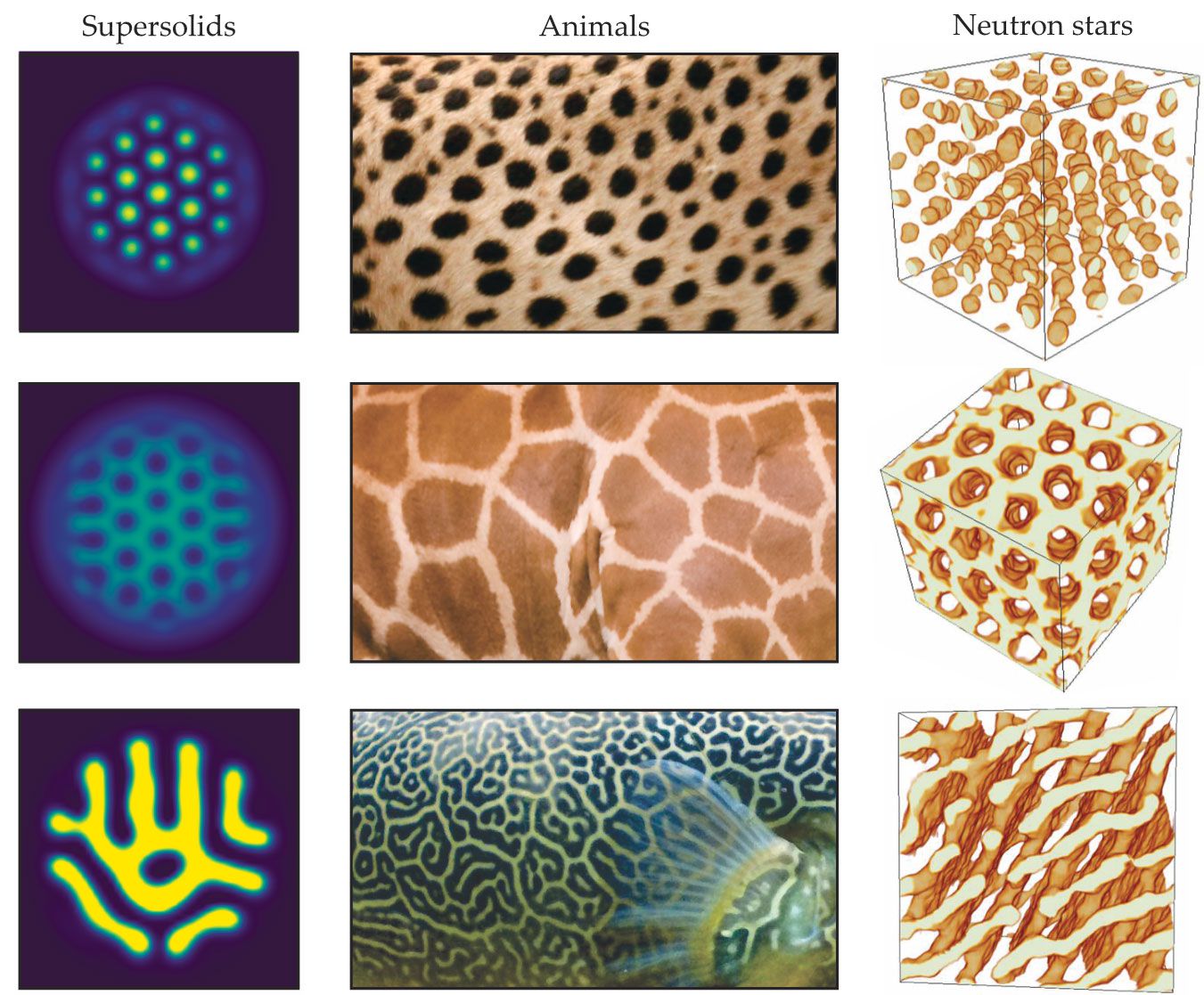
Finally, the observed droplet crystals seem to be, by no means, the only supersolid states possible. Recent theoretical work has established a variety of potential supersolid patterns in dipolar quantum gases. ^{14 , 15} As shown in figure 5, those predicted patterns are reminiscent of those in a range of systems, including the animal kingdom and neutron stars, that cover vastly different energy and length scales. Beyond the fundamental interest in new states of matter and their properties, the observation of supersolid states in dipolar atomic gases could thus provide an unexpected and versatile approach to study pattern formation in the quantum world.

Figure 5.