Arresting soap-bubble flows

Soap bubbles delight and fascinate young children and scientific minds alike. Isaac Newton, Joseph Plateau, Carlo Marangoni, Pierre-Gilles de Gennes, and many others have discovered remarkable results in optics, molecular interactions, and fluid dynamics from studying that seemingly simple system.

In anticipation of the 2016 meeting of the American Physical Society’s Division of Fluid Dynamics this month, Physical Review Fluids recently featured the top posters and videos presented at the previous meeting’s Gallery of Fluid Motion. Among them was a video by Stanford University’s Saad Bhamla and Gerald Fuller on their investigation of the surface flows on a rising soap bubble.

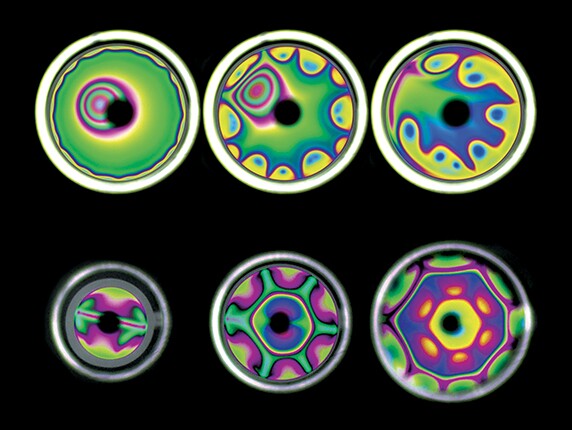
The chaotic flows on the surface of a soap bubble create vibrantly colored, mesmerizing displays as the shifting wall thicknesses alter the interference patterns at visible wavelengths. Named after Marangoni, who studied them in the late 1800s, the flows arise from surface-tension gradients. The top sequence illustrates the effect. When Bhamla and Fuller created a millimeter-diameter air bubble just below the surface of a soap solution and then pushed it up 0.9 mm, the interference patterns they recorded revealed an initially centered, unstable dimple that quickly fled to the periphery, chased by plumes of surfactant. Splitting the rise into three discrete steps of 0.3 mm, however, produced a cascade of instabilities that arrested each other (bottom sequence), and the dynamic flows remained much more symmetric. Beyond their visual appeal, such experiments are relevant for numerous applications, from shampoo development to the treatment of neonatal respiratory distress syndrome. (M. S. Bhamla, G. G. Fuller, Phys. Rev. Fluids 1, 050506, 2016, doi:10.1103/PhysRevFluids.1.050506 ; video at http://dx.doi.org/10.1103/APS.DFD.2015.GFM.V0040 .)