How does light behave in a material whose refractive index vanishes?
DOI: 10.1063/PT.3.4968
The refractive index of a material describes how fast light travels through it. The index is the dimensionless ratio of light’s speed in a vacuum to its speed, or phase velocity, in the material. For a light wave whose temporal variation is given by a frequency
Both of those quantities dictate how light changes shape in space. Following Snell’s law,
Because the refractive index is so prevalent in light–matter interactions, one might wonder how an electromagnetic wave behaves in materials for which
Snell’s law collapses into highly selective angular filtering because only normally incident radiation can penetrate an NZI material. And unusual reflection rules produce mirrors with a reversed phase. Such optically unusual materials open a fundamentally new regime for light–matter interactions, where even the most basic intuition of classical electrodynamics can become distorted. This Quick Study explores a few physical consequences.
Origins
How is it even possible for
Some materials are complex, as we suggested in the introduction, with a refractive index that changes with frequency. Metals are a good example. Their response at optical frequencies can be approximated by
Beyond that simple model, various materials with complex dispersion profiles exhibit a near-zero refractive index in a limited frequency range. Examples include doped semiconductors, polar dielectrics, and transition-metal nitrides. What’s more, metamaterials—electromagnetic constructs whose effective refractive indices emerge from their geometrical structure—can be built with a negative refractive index (see the article by John Pendry and David Smith, Physics Today, June 2004, page 37
Static–dynamic optics
It took the genius of James Clerk Maxwell to unify electricity, magnetism, and light into a single entity—the electromagnetic field. In his dynamical theory, he showed that the spatial and temporal variations of electric and magnetic fields are fundamentally intertwined and give rise to waves that travel at the speed of light in a vacuum. Maxwell’s curl equations
From those equations, it’s clear that as

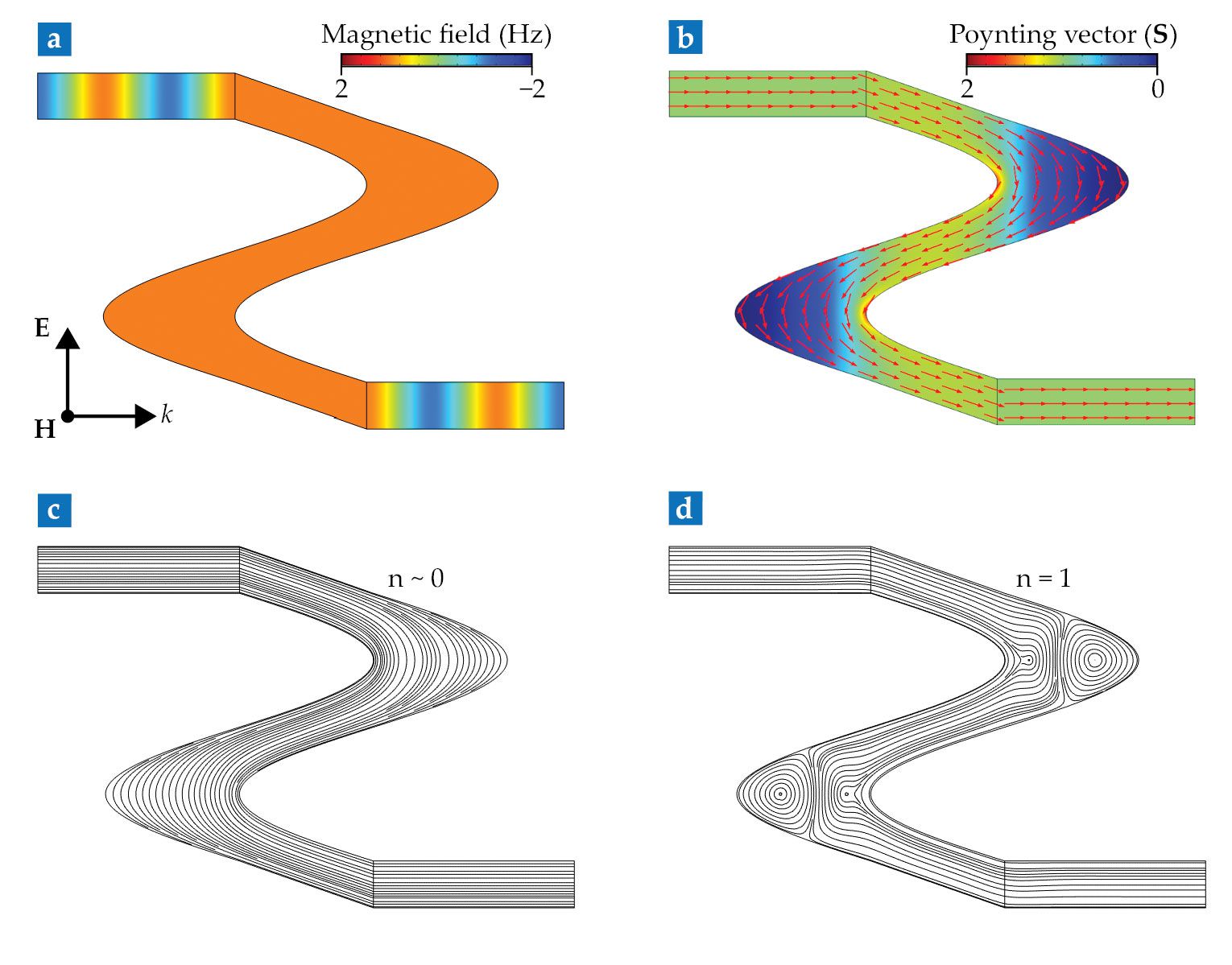
Ideal fluids of light. In a material whose refractive index is near zero (a), the wavelength of light becomes enormous. As a result, the electromagnetic wave becomes completely delocalized and its transmission through a deformed waveguide (orange) perfect—that is, turbulence-free—an effect known as supercoupling. (b) The flow of power and (c) transmission streamlines in the waveguide are equivalent to those of an ideal fluid and inhibit optical turbulence. A light wave entering the deformed waveguide (from left) smoothly adapts to the deformation and suffers no backflow or vortex formation. (d) In a material whose refractive index n = 1, by contrast, vortices typically form in the corners of the waveguide and in the presence of obstacles to the flow.
One consequence of that decoupling between spatial and temporal field variations is that the resonance frequency of an optical cavity can be independent of the geometry of its external boundary. That’s not how resonators are supposed to behave. Waves in an optical cavity typically exist only at specific frequencies where the phase variations satisfy the boundary conditions imposed by the walls of the cavity. But that restriction disappears when the phase is frozen and resonant modes in NZI cavities obey completely different rules. In this newly created class of optical resonators, the geometry of an external boundary confining the optical mode has no effect on the resonance frequency.
In another example, arbitrarily sized dielectric particles immersed in NZI media do not scatter light in the way that conventional materials do. Instead, they act as photonic dopants that modify the effective permeability (see Physics Today, May 2017, page 20
Ideal fluids of light
One surprising aspect of electrodynamics is that power can be transmitted through an NZI body from one region to another. Despite its spatially static character, the electromagnetic field’s time evolution is not halted. Power can be transmitted through NZI media, but it does so in an unexpected way. We recently demonstrated, analytically and numerically, that the Poynting vector field
So far as power flow is concerned, NZI media can therefore be regarded as a perfect electromagnetic fluid—incompressible, inviscid, and irrotational, characterized by a total inhibition of turbulence. For that reason, light in NZI media flows smoothly and circumvents any obstacles in the way. As shown in the figure, the flow doesn’t generate any vortices or reflection.
The concept of an ideal fluid provides a fresh perspective on one of the most iconic NZI phenomena—supercoupling. Typically, when a field propagating in a waveguide encounters a deformed section, part of the incident power is reflected backward. But if the deformed section is filled with NZI material, the power can be efficiently transmitted through it without experiencing any scattering.
The effect takes place independently of the geometry of the deformed section and can be understood as a consequence of wavelength enlargement. Indeed, the wavelength becomes so large that the entire deformed, NZI-filled section becomes effectively compressed in space, much like an electromagnetic point. Input and output ports of the deformed waveguide become connected; waves in one section can tunnel, unimpeded, into another.
Electromagnetic fluids in NZI materials can be considered a bridge between fluid dynamics and electrodynamics. They offer multiple crossbreeding opportunities. The application of airfoil theory to scattering systems, for example, might reveal new forms of optical manipulation. In addition, optical systems in which turbulence is intrinsically inhibited might also enable high-precision metrology systems to operate under harsh mechanical conditions.
References
► I. Liberal, N. Engheta, “Near-zero refractive index photonics,” Nat. Photonics 11, 149 (2017). https://doi.org/10.1038/nphoton.2017.13
► O. Reshef et al., “Nonlinear optical effects in epsilon-near-zero media,” Nat. Rev. Mater. 4, 535 (2019). https://doi.org/10.1038/s41578-019-0120-5
► N. Kinsey et al., “Near-zero-index materials for photonics,” Nat. Rev. Mater. 4, 742 (2019). https://doi.org/10.1038/s41578-019-0133-0
► I. Liberal et al., “Near-zero-index media as electromagnetic ideal fluids,” Proc. Natl. Acad. Sci. USA 117, 24050 (2020). https://doi.org/10.1073/pnas.2008143117
► I. Liberal et al., “Photonic doping of epsilon-near-zero media,” Science 355, 1058 (2017). https://doi.org/10.1126/science.aal2672
► I. Liberal, A. M. Mahmoud, N. Engheta, “Geometry-invariant resonant cavities,” Nat. Commun. 7, 10989 (2016). https://doi.org/10.1038/ncomms10989
More about the Authors
Iñigo Liberal is a Ramón y Cajal fellow and European Research Council Starting Grant holder at the Public University of Navarre in Pamplona, Spain. Nader Engheta is the H. Nedwill Ramsey Professor of Electrical and Systems Engineering at the University of Pennsylvania in Philadelphia.






