Going with the flow in unstable surroundings
DOI: 10.1063/pt.zork.luqw
As children, we learn to stack simple symmetrical shapes and use them to create patterns. A sense of order and repetition sways our ideals of perfection. But, as English writer W. Somerset Maugham wrote in The Summing Up, “But perfection has one grave defect: it is apt to be dull.”
Nature, though, is rarely dull. It is full of patterns that are imperfect or disordered. Although patterns appear at different scales and in different contexts, they often have underlying rules that govern their growth. For example, tree branches, plant roots, and river networks share similar branching features. As experimentalists, we aim to uncover the physics that governs the branching observed in nature by reproducing patterns in the controlled environment of the lab.
For branching patterns, the archetypal system of study is an unstable fluid-flow phenomenon called viscous fingering. It occurs when a less viscous fluid, such as water, invades a more viscous fluid, such as honey, in a confined space—for example, the thin gap between two plates. The inner, low-viscosity fluid contacts the outer fluid at an interface that is initially smooth. But the flow is unstable: Any small distortion, caused by a molecular-level pressure variation or even a mote of dust, becomes amplified. Those initially small perturbations eventually cause undulations to form along the interface. Small, protruding sections of the inner fluid grow faster than neighboring regions and form long fingers.
We can re-create such finger patterns using an experimental apparatus called a circular Hele-Shaw cell, which consists of two flat, round glass plates separated by a thin gap. The size of the gap determines the fluid confinement. In our experiments, we use two fluids that are miscible with each other so that there is negligible surface tension between them. The more viscous fluid, followed by the lower-viscosity one, is injected through a small hole in the center of the top plate. The resulting radial flow is imaged from below the plates. By dyeing one of the fluids, the boundary between the two is visible.
For decades, researchers have largely restricted themselves to observing how finger patterns form at the interface. Few have examined what happens beyond it—namely, how the flow of the incoming and the outgoing fluid interacts with the branching finger structures. Understanding those interactions requires probing the fluid flow everywhere in the cell. We therefore redesigned our experiments to allow us to peer at the fluid behind and the fluid beyond the patterns forming at the interface.
Designing the technique
It can be difficult to measure flow in confined systems like the Hele-Shaw cell. In our technique, we first inject into the cell the more viscous, transparent outer fluid, which appears as the white outer region in figure
Figure 1.

Branching patterns formed by viscous fingering. Low-viscosity inner fluid, visible in shades of blue, is injected in alternate rings into a more viscous, transparent outer fluid. Fingers grow at the unstable interface between the two fluids. Undulations along the rings of dyed fluid reveal the influence of local pressure gradients.
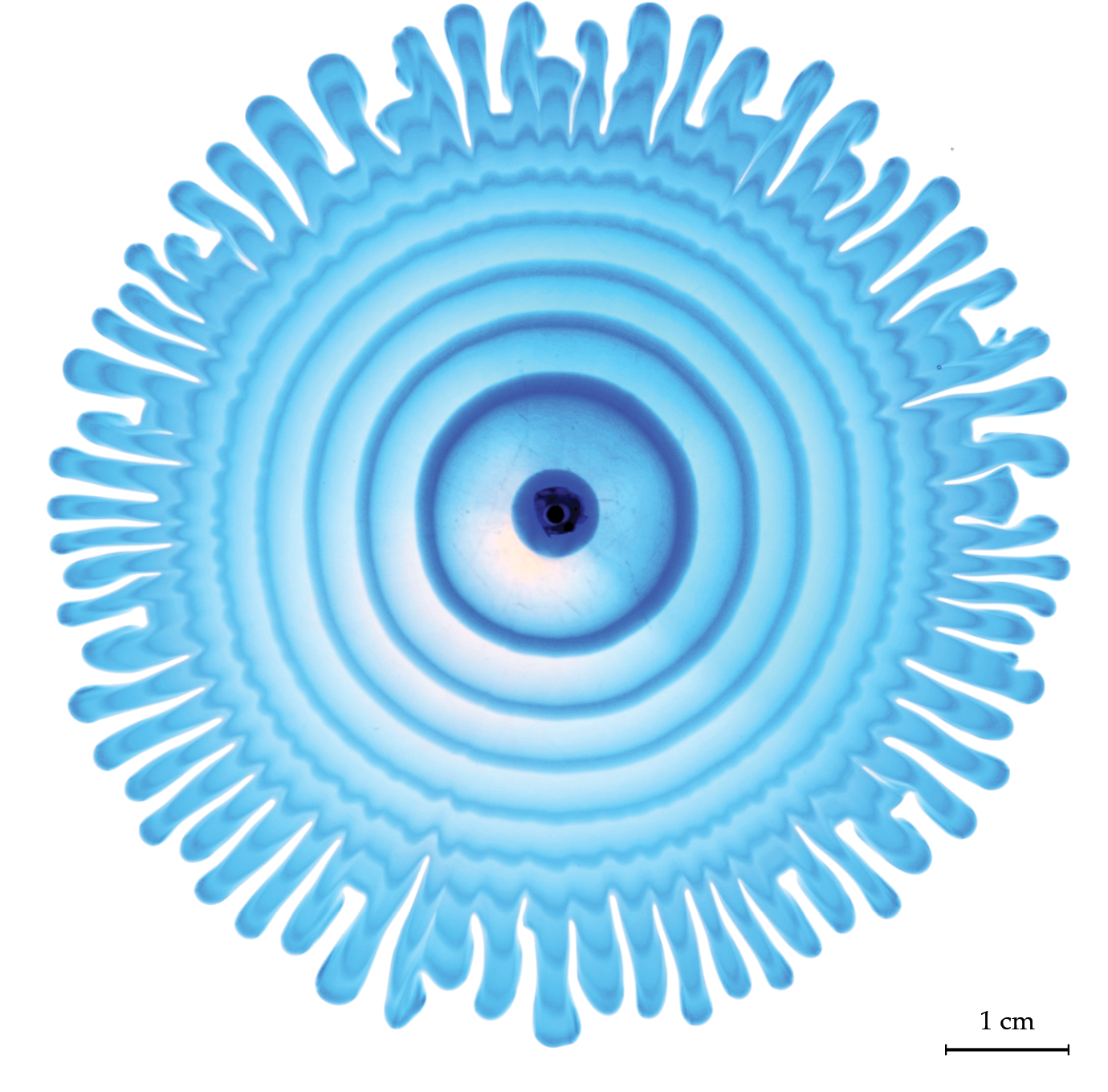
Not only does the technique create an elegant visualization of the patterns shown in figure
Figure
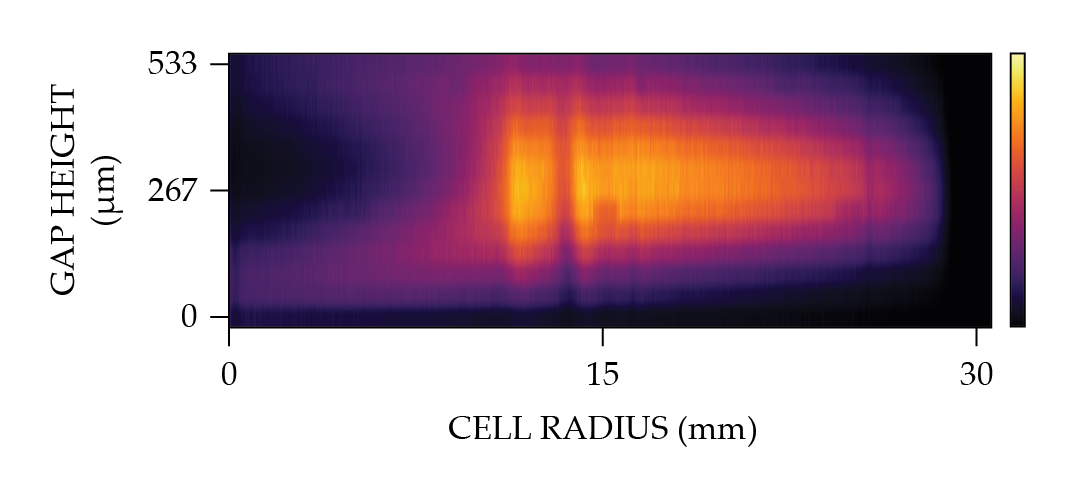
Figure 2.

Confocal imaging of a dyed fluid ring in the gap of a Hele-Shaw cell. Fluorescently dyed fluid is injected alternately with undyed fluid between two glass plates. The fluid between the gap is imaged using a confocal microscope. The aspect ratio has been exaggerated along the y-axis because the height of the gap is much smaller than the radius of the cell. The highest pixel intensity is observed at the center of the gap, where the dyed fluid is most concentrated.
Memorably perturbed
Figure
The appearance of those imperfections indicates local pressure gradients that, although seeded at the interface, can affect flow up to several centimeters behind it. We can characterize that length and observe how it evolves dynamically with the patterns. The same persistence of local pressure variations is revealed in the outer fluid when we employ an alternate injection technique, in which the outer fluid is dyed.
The technique we developed allows us to measure the flow dynamics for a system that is otherwise hard to access by simulation or experiment. As it turns out, the tiny pressure perturbations that seed the instability cause increasing flow distortion long after the patterns first emerge and reveal a hidden length scale over which local pressure gradients matter. We suspect that may be relevant to understanding other branching phenomena.
In the end, our unstable system looks a lot more enticing than its stable counterpart, a perfect circle. All the small perturbations and disturbances added together form a natural beauty perhaps more memorable than mere perfection.
References
► S. D. Gowen, T. E. Videbæk, S. R. Nagel, “Measurement of pressure gradients near the interface in the viscous fingering instability,” Phys. Rev. Fluids 9, 053902 (2024). https://doi.org/10.1103/PhysRevFluids.9.053902
► I. Bischofberger, R. Ramachandran, S. R. Nagel, “Fingering versus stability in the limit of zero interfacial tension,” Nat. Commun. 5, 5265 (2014). https://doi.org/10.1038/ncomms6265
► Y. Couder, “Viscous fingering as an archetype for growth patterns,” in Perspectives in Fluid Dynamics: A Collective Introduction to Current Research G. K. Batchelor, H. K. Moffatt, M. G. Worster, eds., Cambridge U. Press (2000), p. 53.
► G. M. Homsy, “Viscous fingering in porous media,” Annu. Rev. Fluid Mech. 19, 271 (1987). https://doi.org/10.1146/annurev.fl.19.010187.001415
More about the authors
Savannah Gowen is a graduate student and Sidney Nagel is an experimental soft-matter physicist and Gowen’s research adviser in the department of physics at the University of Chicago. Thomas Videbæk is an experimental soft-matter physicist in the Martin A. Fisher School of Physics at Brandeis University in Massachusetts.







