Toward an attosecond view of molecules
DOI: 10.1063/PT.3.1544
Femtosecond spectroscopy was a landmark development in chemical and molecular physics: It allows the motion of atoms, including the breaking and forming of chemical bonds, to be monitored in real time. (See PHYSICS TODAY, December 1999, page 19
A key ingredient in every attosecond experimental technique so far has been ionization or probing by a strong laser field. In the prevailing model of strong-field ionization (SFI), used to interpret experimental results, it’s assumed for simplicity that only one electron—the one with the highest energy—feels the pull of the ionizing laser field. Perhaps surprisingly, that model works well when applied to noble-gas atoms and some small molecules. But for larger molecules, which host many of the electronic processes researchers want to study, it can fail badly.
Now, Albert Stolow (National Research Council Canada) and colleagues report that they have developed an experimental technique for studying subcycle SFI in polyatomic molecules. 1 In the same paper, Council theorists Michael Spanner and Serguei Patchkovskii present an ab initio method for solving the time-dependent Schrödinger equation for a polyatomic molecule in a strong laser field. Applied to two different four-carbon hydrocarbon molecules, the experiment and theory agree well, and both show that several electrons participate in the attosecond-scale ionization.
Ultrafast ionization
An extreme nonlinear process, SFI involves a highly focused laser beam. When the laser’s electric field varies slowly relative to the time scale of electron motion, the Coulomb potential of the atom or molecule tilts, as shown in figure 1a, to the point where an electron can tunnel through the potential barrier and escape. Because tunneling probability is exponentially related to the barrier height, ionization only happens at the very peak of the laser field oscillation, as shown in figure 1b. So a visible or near-IR laser beam, with a period of several thousand attoseconds, can create subcycle bursts of ionization lasting only about 100 as.
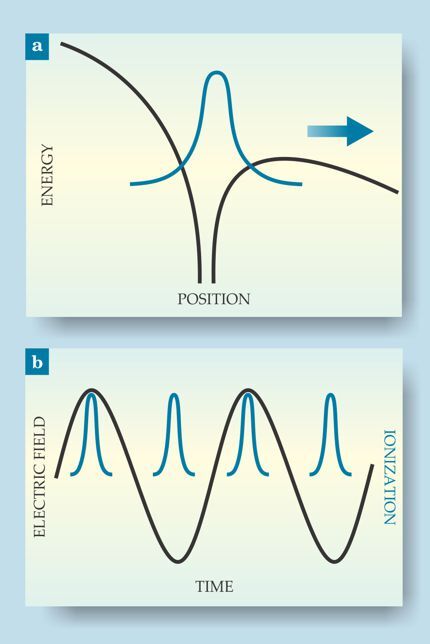
Figure 1. Strong-field ionization of an atom or molecule. (a) The electric field of a highly focused laser pulse tilts the Coulomb potential (black) until one of the electrons (blue) can tunnel through the barrier and escape. (b) The tunneling rate depends exponentially on the field strength, so attosecond ionization events (blue) can result from a much slower laser oscillation (black).
One can do several things with SFI, depending on whether the laser pulse consists of one oscillation or several and whether it drives the electron and parent ion to recollide or pulls them apart forever. (See the articles in PHYSICS TODAY by Paul Corkum, March 2011, page 36
The model usually invoked to understand those dynamics was developed by Paul Corkum in 1993. It’s based on three assumptions: Electrons respond instantaneously to changes in the laser field; tunneling proceeds instantaneously; and only the most weakly bound electron is involved, or “active,” in the ionization. 2 Those assumptions made computational modeling feasible. But Stolow had long suspected that their validity was limited to atoms and small molecules.
Beginning in 2001, Stolow and his group published a series of papers 3 showing that the rate of SFI of polyatomic molecules and of transition-metal atoms and clusters can be orders of magnitude different from what’s predicted by Corkum’s model. But working backward from the measured ionization rates to a real understanding of SFI dynamics would have required intense modeling—and knowing which assumptions were valid for doing that modeling would have required already having an understanding of what was going on. Multiple active electrons were a possible explanation. Curiously, in metal atoms and clusters, they make the ionization slower, not faster: As several electrons move toward the barrier, they raise the effective barrier height for the one that ends up escaping. But not all theorists were convinced. Many thought that the single-active-electron model was still right, but it just needed some refining.
Multiple active electrons
Stolow and colleagues’ experimental method probes SFI in molecules without the need for modeling. For their demonstration, the researchers looked at two hydrocarbon molecules, one of which was butane, shown in figure 2a. Removing the highest-energy, most weakly bound electron puts the molecular ion, C4H10+, in its ground state. Removing a lower-energy electron yields a higher-energy ionic state. All of ionized butane’s excited states are inherently unstable, with the parent ion spontaneously breaking apart into smaller fragments, as shown in figure 2b. Observing one of those smaller ions is a sign that subcycle SFI is removing one of the lower-energy electrons.

Figure 2. The case for multiple-electron participation in strong-field ionization of butane. (a) Butane’s chemical structure. (b) Ionized butane may remain intact, or it may break into smaller fragments. Only the ground ionic state remains intact. Excited ionic states, created by removing electrons other than the most weakly bound one, all fragment. (c) Kinetic-energy spectra of the electrons measured in coincidence with the intact and fragment ions. Peaks correspond to photons absorbed in excess of the ionization threshold. The phase shift in the spectra (black arrows) shows that different ionic states are formed and different electrons are removed. (Panel c adapted from ref.
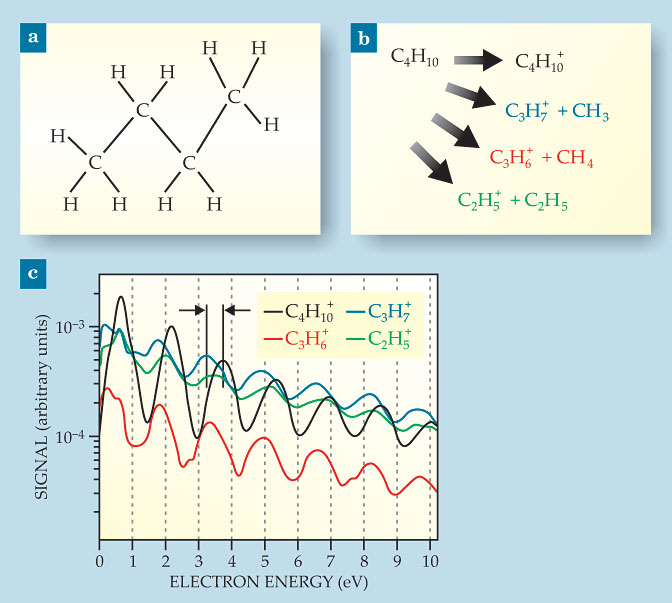
But it’s not definitive proof. It’s also possible that the ion is created in its ground state but a later cycle of the same laser pulse promotes it to an excited state. To rule out that possibility, the experimenters measured not just the mass of the remaining ionic fragment but also the kinetic energy of the departing electron in coincidence with the ion. When the molecule absorbs more photons than are needed for ionization, the excess energy is taken up by the electron. The electron kinetic-energy spectrum therefore displays a series of peaks. The spacing between peaks is equal to the laser photon energy, and their absolute position depends on how much energy went into ionization.
In their butane experiment, Stolow and colleagues assigned electrons to one of four spectra, shown in figure 2c, depending on which ion they observed. If SFI always removed the most weakly bound electron but later laser cycles promoted some of the C4H10+ ions into unstable excited states, all four of the electron–ion coincidence kinetic-energy spectra would be in phase.
That they’re not in phase, as shown by the black arrows in figure 2c, is proof that it’s not always the highest-energy electron being removed, and thus several electrons must be active in the subcycle ionization event. The C4H10+ spectrum position is consistent with
formation of the ground ionic state—as it must be, because that’s the only state of C4H10+ that doesn’t fragment. The C3H7+ and C3H6+ spectra are in phase with each other, but they are shifted by 0.4 eV from the C4H10+ spectrum, consistent with the energy of the first excited ionic state. The C2H5+ spectrum is not in phase with any of the others, and its peaks are less pronounced, but it may result from formation of the third excited state.
Computational corroboration
To complement Stolow’s experiment, Spanner and Patchkovskii studied the same ionizations computationally, without using any adjustable parameters. The method they developed bridges the gap in complexity between the single-active-electron methods traditionally used in attosecond research and the powerful tools for computing electronic stationary states in quantum chemistry. (See the article by Martin Head-Gordon and Emilio Artacho in PHYSICS TODAY, April 2008, page 58
References
1. A. Boguslavskiy et al., Science 335, 1336 (2012). https://doi.org/10.1126/science.1212896
2. P. B. Corkum, Phys. Rev. Lett. 71, 1994 (1993). https://doi.org/10.1103/PhysRevLett.71.1994
3. M. Lezius et al., Phys. Rev. Lett. 86, 51 (2001); https://doi.org/10.1103/PhysRevLett.86.51
M. Smits et al., Phys. Rev. Lett. 93, 213003 (2004); https://doi.org/10.1103/PhysRevLett.93.213003
M. Smits et al., Phys. Rev. Lett. 93, 203402 (2004).https://doi.org/10.1103/PhysRevLett.93.203402
More about the Authors
Johanna L. Miller. jmiller@aip.org




