The universal statistics of random searches

How efficient can an exhaustive search be? Whether the goal is to locate every mushroom in a forest, say, or specific sequences on a DNA strand, the cover time τ—defined as the time it takes for a random walk to find all the targets in a spatial network—can quantifiably answer that question. But despite τ’s relevance to a broad range of situations, from animals foraging for food to diseases spreading through a city, analytical results have been scarce and mostly limited to regular random walks—those involving moves between nearest neighbors in Euclidean geometry.

Not all random trajectories look the same, and in more complex strategies, the random walker’s movement among neighbors differs from diffusive Brownian motion: It can be “persistent,” for instance, weighted toward a particular direction that depends on a previous step; be “intermittent,” stepping between nearest neighbors at one rate and leapfrogging over them at another rate to resume the search elsewhere; or take so-called Lévy flights, which jump from one region to another with step lengths that follow a power-law distribution. (See the article by Joseph Klafter, Michael Shlesinger, and Gert Zumofen, Physics Today, February 1996, page 33 .)

For those and other complex strategies, researchers have focused almost entirely on the time required to reach a single target—the first-passage time T—and have set aside the much harder problem of determining τ. Now CNRS theorists Marie Chupeau, Olivier Bénichou, and Raphaël Voituriez have linked the two quantities and analytically derived the probability distribution of τ for several different complex random-walk processes on a finite lattice network. ¹

After first writing an expression for τ in terms of a sum of the individual times needed to find each new target among the unfound ones on the lattice, the theorists made a bold hypothesis: Although those individual times depend on the entire random trajectory the walker has taken—and are thus correlated—they can be treated as independent variables, provided the number of targets N is large. Armed with that hypothesis, which they later checked numerically, the CNRS researchers exploited the fact that the distribution of the “global” first-passage time ⟨T⟩—that is, the mean value of T averaged over all starting positions—is an exponential. That, in turn, led them to an expression for τ’s probability distribution, plotted on page 18.

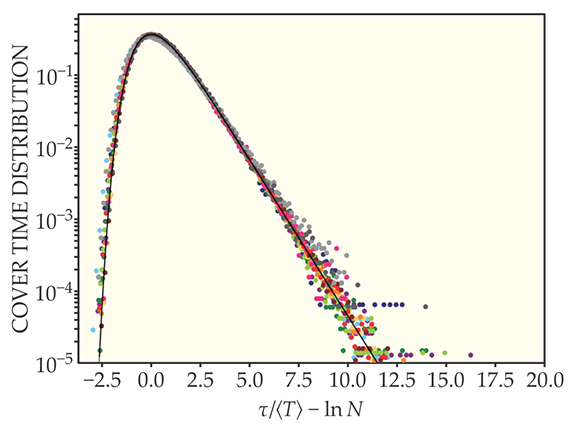
Remarkably, Chupeau and her colleagues found that when τ is rescaled in terms of the global first-passage time, its probability distribution becomes universally applicable to any of the several complex search strategies the theorists considered. That is, although τ itself is dependent on the dimensionality and connectivity of the network and the specific rules a random walker follows to search it, the probability distribution for τ/⟨T⟩ is completely insensitive to them: All the data points the researchers obtained by numerically simulating the different strategies fall on the same curve.

After deriving the distribution, the team recognized its resemblance to the so-called Gumbel distribution, used to model extreme-value problems such as the likelihood of an electric current fluctuating above some critical threshold or the chances of a river reaching flood stage. That the distribution of cover times should follow the same statistics isn’t entirely unexpected since τ, by definition, is the time it takes to find all the targets in a given domain and is thus the largest of the arrival times at each target. The bigger surprise is that short-time dynamics, in which correlations between time and trajectory are important, become irrelevant. So much greater is the time needed to find the last few targets in the limit of a large number of them that the correlations are apparently negligible to the statistics.

That’s not to say that one search strategy isn’t more efficient or better suited for a particular problem than another. To determine the distribution, mean, most probable value, or variance of τ for a specific strategy, one needs only to reverse the scaling in the plotted distribution. What’s more, thanks to that direct and robust connection between first-passage and cover times, the researchers found that if you optimize search parameters to minimize ⟨T⟩, you will have automatically also minimized τ. As Voituriez puts it, “One and the same strategy minimizes both times—an entirely unexpected result.”