The hydrodynamics of a quantum fluid

Hydrodynamics deals primarily with the flow of water and other fluids. A branch of fluid dynamics, it describes the behavior of many-body systems, from molecules in a cup of tea to cars on a highway. The framework, which assumes that each point in a fluid-like collection of particles is locally at equilibrium, characterizes the local quantities that are conserved for an entire system. For a classical fluid like water, those local quantities are mass density, momentum density, and energy density. Models encode the evolution of local quantities in the form of continuity equations based on mass, momentum, and energy conservation.

In the quantum world, many-body systems are notoriously difficult to model because the computational memory needed to retain their characteristics grows exponentially with the number of particles. Instead of trying to describe the complex movement of each individual particle, quantum theorists seek ways to explain many-body systems in terms of a reduced number of local characteristics. Hydrodynamics offers an appealing tool.

However, hydrodynamical models work only for systems that quickly forget the details of their initial configuration—that is, those that reach thermal equilibrium without any external influence. For example, each small parcel of water in a bucket reaches a local equilibrium because the motion of the molecules is chaotic. Through collisions, the water molecules’ mechanical, chemical, and thermal parameters quickly reach constant values.

The same models fail to explain the dynamics of systems that retain a memory of their initial state and don’t reach thermal equilibrium. One-dimensional collections of ultracold atoms offer an opportunity to study that very selected class of systems. Because of the oddities of quantum physics, the atoms in such systems not only collide with each other, they also pass through one another. Collisions among particles cannot change the velocity distribution of the fluid and bring about thermal equilibrium.

Since the early 2000s, experiments with 1D collections of weakly interacting bosons, or Bose gases, have inspired theorists to develop models of nonequilibrium quantum particle transport. Only in the past two years have quantum theorists proposed a form of hydrodynamics that extends to nonequilibrium systems.

Now Max Schemmer, Isabelle Bouchoule (both at the University of Paris-Saclay), and their colleagues have provided the first direct evidence in support of new hydrodynamic models that are sufficiently general to describe the nonequilibrium behavior of ultracold atoms albeit in one dimension. ¹

Motus aeternus

An experiment known as the quantum Newton’s cradle, published in 2006 by David Weiss and colleagues at the Pennsylvania State University, ² motivated a series of efforts to model the observed behavior of nonequilibrium quantum particles. The classical Newton’s cradle is a familiar desktop toy that involves several steel balls, suspended in a row by wires. When one ball is set swinging, it hits the other balls and its momentum is transferred until the ball at the opposite end swings away while the intermediate balls remain stationary. In the quantum version, tens to hundreds of ultracold rubidium atoms replace the steel balls, and lasers confine the atoms in an elongated trap to create a 1D system. Additional lasers set the atoms into motion and cause them to oscillate like the desktop toy.

The quantum Newton’s cradle was a first surprising experimental finding of many interacting particles that showed undamped motion. The motion continued undamped over thousands of collisions and the atoms did not reach thermal equilibrium.

The underlying equations of motion that describe the quantum Newton’s cradle are based on Elliott Lieb and Werner Liniger’s 1963 paradigm for describing the interaction strengths in a cloud of ultracold atoms constrained to a straight line. ³ Solving those deterministic equations could in principle predict all the motion-related properties of the particles at any time in the past and the future.

But for clouds of atoms larger than 20 particles, describing the time evolution of the system becomes too complex to solve on a classical computer. “Starting from Newton’s cradle, thousands of theoretical papers have tried to simulate what happens for larger numbers of atoms,” says Bouchoule.

Generalized hydrodynamics

In 2016 both Olalla Castro Alvaredo (City, University of London) and collaborators ⁴ and Bruno Bertini (International School for Advanced Studies in Italy) and collaborators ⁵ proposed an efficient way to describe the dynamics of nonequilibrium 1D quantum systems. Instead of explicitly detailing the dynamics of each particle, the research teams adopted a hydrodynamics approach, conceptually zooming out so that the particles appeared as one continuous fluid. The new framework helped to model experiments and theoretical situations that were previously beyond description.

Hydrodynamical descriptions of particle number, momentum, and energy density suffice to model the time evolution of a quantum system that reaches thermal equilibrium. But a system that in theory never reaches thermal equilibrium—like the undamped oscillations of the classical and the quantum Newton’s cradle—has a distribution of quasiparticle velocities. An infinite number of densities must be globally conserved, each of which is characterized in the form of a continuity equation. Careful mathematical representation of the particles’ momenta made it possible to identify a set of equations that represent the continuity of all the conserved quantities. Hydrodynamics adapted for an infinite number of conserved quantities is known as generalized hydrodynamics, and it offers a way to predict the behavior of systems that remember their initial state.

Not just a conjecture

The quantum Newton’s cradle and other 1D quantum systems are real-world scenarios in which generalized hydrodynamics should apply, but until now the framework remained a hypothesis. Schemmer’s new work, says Weiss, “provides the first explicit experimental application of generalized hydrodynamics.”

To test the theory, Schemmer and colleagues confined several thousand cold ⁸⁷Rb atoms in a magnetic trap built on a chip, shown in figure 1. The trap comprised three parallel conducting wires several millimeters long. The atoms were guided 15 μm above the wires, and the large magnetic field gradient provided strong confinement along the y- and z-axes. Four longer wires, parallel to the y-axis, provided weak confinement along the x-axis. By suddenly turning off the current in the longer wires, the researchers could relax the longitudinal confinement and free the atoms to flow along the x-axis.

Figure 1.

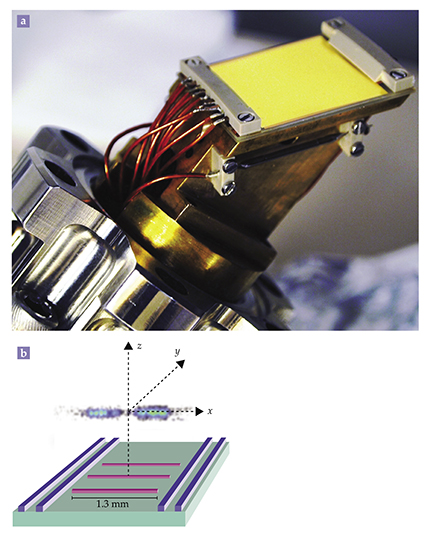
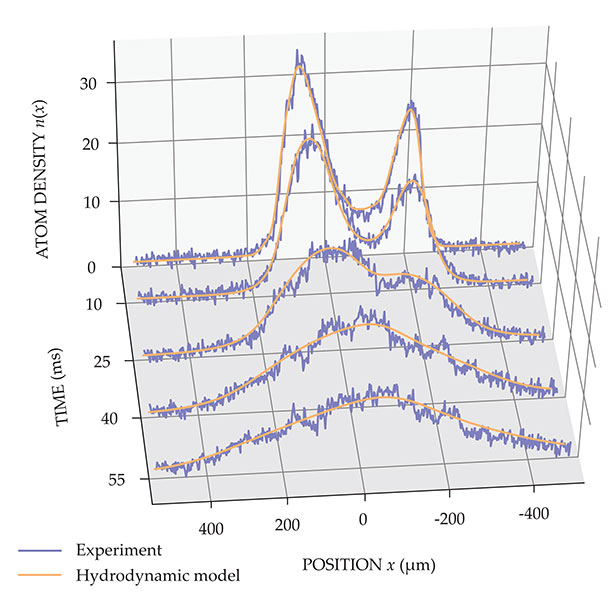
The researchers tested several initial configurations, such as the two separate peak-density locations shown in figure 2. When the confinement was relaxed, the atom density n(x) evolved into a smooth distribution, as predicted by generalized hydrodynamics, rather than maintaining the two peaks. In contrast, conventional hydrodynamics models applied to the same situation wrongly predicted that the atoms would develop two large density waves.

Figure 2.

However, when the atoms started from a single initial density peak and the system was at thermal equilibrium, both conventional and generalized hydrodynamics made the same successful prediction: that the atoms would evolve into a broad distribution when allowed to expand freely in one dimension. The experiment confirmed that the generalized model’s infinite coupled equations reduced to the finite equations of the conventional model.

The study also addressed the quantum Newton’s cradle. In a configuration that mimicked the Weiss group’s original 2006 experiment, Schemmer and Bouchoule released atoms from a double-peak distribution then immediately set them into harmonic oscillation. In that situation, conventional hydrodynamics models mistakenly predicted that shock waves should develop in the experiment. Generalized hydrodynamics predicted what was observed: The atom density oscillated between one and two peaks.

Theory and experiment did not conform perfectly, though. At later times (hundreds of milliseconds), atomic density distributions began to deviate slightly from the generalized hydrodynamics prediction. Schemmer and Bouchoule attributed the deviation to the gradual leakage of atoms from the trap over the course of the experiment.

Paradoxically, it takes a specialized experimental system to realize the infinite conservation laws of generalized hydrodynamics. Bertini, one of the founders of generalized hydrodynamics, says that “the compromises adopted to experimentally realize a system describable by the theory have left both experimental and theoretical open questions.” Those questions include what the behavior is of multicomponent ultracold gases and of clouds of atoms that are more strongly repulsive than rubidium. Still, Hendricus Stoof at Utrecht University in the Netherlands says the new experiments verify that generalized hydrodynamics “really works in the lab and is not just a weird conjecture from theorists.”