Testing the doubly magic character of tin-132
DOI: 10.1063/1.3480064
The shell model of nuclear structure predicts that nuclei with certain magic numbers of protons or neutrons will be more rigidly spherical and stable than their neighbors. The magic numbers—2, 8, 20, 28, 50, 82, and 126—are somewhat reminiscent of the atomic numbers of the noble gases, as well they should be. Just as completed shells of single-electron states convey extraordinary chemical stability, completed shells of single-neutron or singleproton states in the mean-field potential of all the other nucleons do much the same for nuclei.
With magic numbers of both protons (Z) and neutrons (N), the four stable “doubly magic” nuclei, helium-4, oxygen-16, calcium-40, and lead-208, are among the most abundant in nature. All four have had their expected doubly magic properties confirmed in the laboratory, as have two doubly magic unstable species with long half-lives: calcium-48 and nickel-56. Just having nominally magic values of Z and N is not sufficient proof of shell closure. As neutron or proton excesses take nuclides further from the valley of nuclear stability (see figure 1), the validity of the shell model becomes an open question that requires testing.
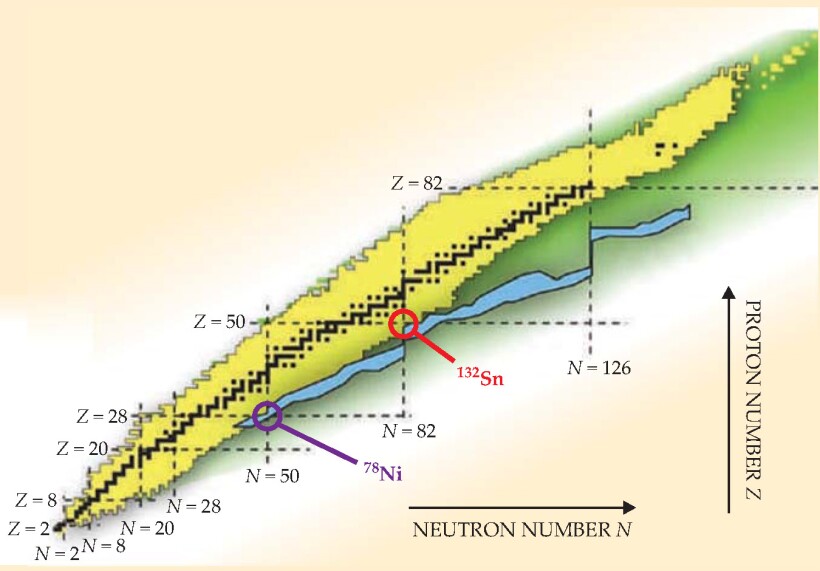
Figure 1. All known nuclides are shown black (if stable) or yellow (unstable). Dashed lines indicate magic numbers of protons and neutrons. Where they intersect, the nuclides are called doubly magic. Two of those, tin-132 and nickel-78, are adjacent to the r-process region (blue) of as-yet-unseen nuclides that are thought to be involved in the creation of the heaviest elements in supernovae.
(Adapted from
Of the few other known nuclides with doubly magic numbers, tin-132 has in recent years been of particular interest to experimenters. Short-lived 132Sn, with its excess of 8 neutrons over the nearest stable Sn isotope, would test the limits of the shell model. And beyond the specific concerns of nuclear-structure theory, 132Sn draws the attention of astrophysicists because, as shown in figure 1, it sits adjacent to the so-called r-process region.
The r process (“r” for rapid neutron capture) in extreme astrophysical environments such as supernovae is presumed to be the principal means by which elements heavier than iron are created. In the presence of sufficiently high neutron fluxes, nuclei can accumulate extra neutrons faster than they can beta decay. (See the article by John Cowan and Friedrich-Karl Thielemann in Physics Today, October 2004, page 47
For all its promise, 132Sn presents experimenters with daunting problems. Its half-life is only 40 seconds. So one can’t perform the conventional test of bombarding a solid target of the material with neutrons to see if they fall into the valence orbits one would expect to form around a rigidly spherical core. The much more demanding alternative of capturing neutrons by running a beam of freshly made 132Sn nuclei into a deuterium target requires, among other highly specialized facilities, the means to deal with the hazardous profusion of long-lived actinides that would accompany the creation of a sufficiently intense beam.
“At present, there’s only one lab in the world that can do that kind of 132Sn experiment,” says Paul Cottle of Florida State University. “That’s the Holifield Radioactive Ion Beam Facility at Oak Ridge.” And indeed Kate Jones (University of Tennessee, Knoxville) and coworkers at Oak Ridge National Laboratory have now reported 1 the results of just such an experiment that confirms and details the doubly magic character of 132Sn.
Why bother?
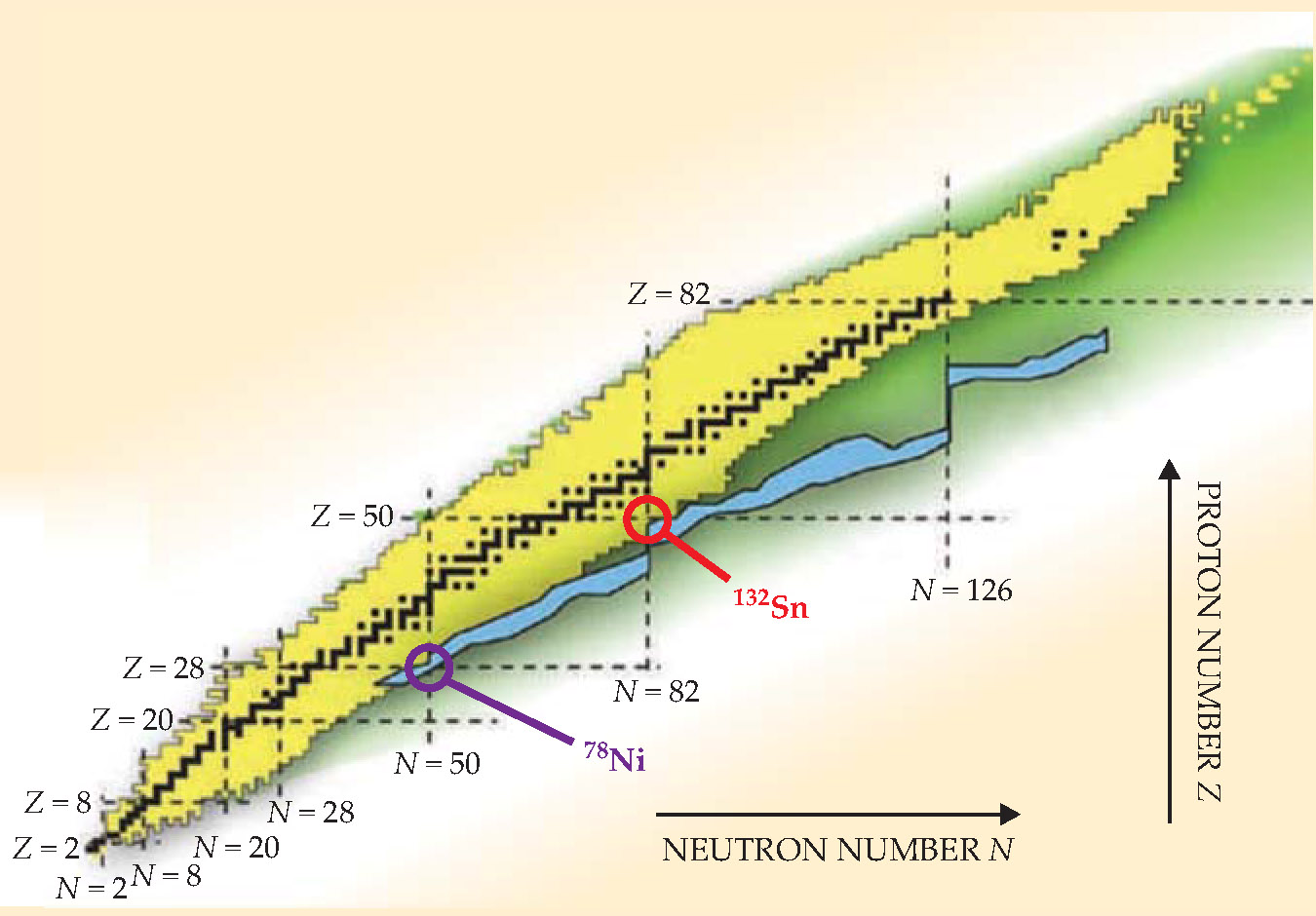
Figure 2 shows two properties of doubly magic nuclei that are much easier to measure than the valence states of extra neutrons. From archival data for various isotopes of Sn and Pb, figure

Figure 2. Doubly magic nuclides tin-132 and lead-208 clearly manifest special properties when compared, from archival data, with lighter isotopes that also have even neutron numbers N. (a) The energy of the first electric-quadrupole excitation peaks dramatically at N magic (82 for Sn, 126 for Pb). (b) The energy cost of removing a neutron pair falls abruptly after N magic.
(Adapted from
So why go to all the trouble of examining the states into which a neutron added to 132Sn falls? “Because, as has become clear in recent years, some doubly magic nuclei are more magic than others,” explains theorist Witold Nazarewicz, scientific director of the Holifeld facility. “The departure of the extra neutron’s spectrum from what’s expected for a rigid spherical core of closed shells is an important measure of polarizing shape vibrations that mix core and valence states. And the observations let us calibrate our nuclear-structure models in r-process regions where direct data will perhaps never be taken.”
In the Oak Ridge experiment, the 132Sn beam began with intense proton bombardment of a uranium target. From the great variety of fission products thus produced, electromagnetic mass separation culled the desired 132Sn ions for acceleration to 630 MeV in the Holifield lab’s tandem Van de Graaff accelerator (see the cover of this issue).
The resulting beam was focused onto a deuterium-rich target, which served as the neutron donor. A surrounding detector array recorded the energies and directions of protons emerging from the desired neutron-transfer reaction
The proton measurements suffice to determine the reaction’s center-of-mass scattering angle θ as well as Q, the increase of total kinetic energy from the initial to the final state. The “heat of reaction” Q reflects the binding energy of the 133Sn valence state in which the transferred neutron has landed.
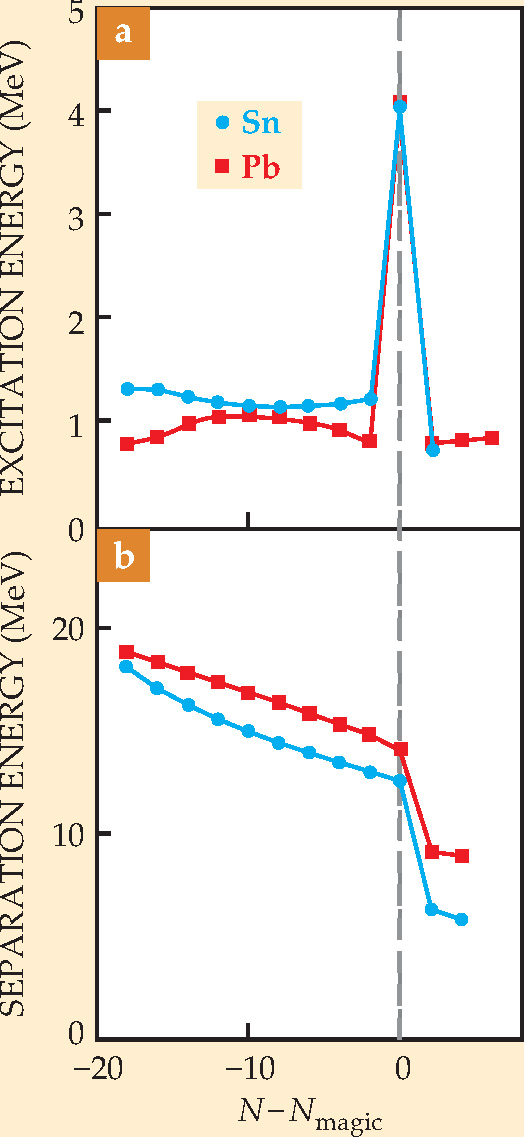
The four peaks in the Q distribution shown in figure 3, measured at one particular θ, indicate the ground state of the extra neutron and three excited states. The figure lists the best-fit excitation energies above the ground state. The fact that the ground state, unlike the excited states, peaks at Q > 0 means that the transferred neutron is more deeply bound in the 133Sn ground state than it was in the loosely bound deuteron.

Figure 3. Distribution of Q , the reaction heat of the neutron-transfer reaction described in the text, measured at a fixed center-of-mass scattering angle θ in an experiment at Oak Ridge National Laboratory. The four peaks indicate the valence ground state and three excited states in which transferred neutrons land to form 133Sn nuclei. Fitted curves assume Gaussian error distributions, and yield the excitation energies (relative to the ground state) listed in the color key.
(Adapted from
Valence-state purity
The absolute and relative peak heights in figure 3 depend on the θ at which the Q distribution was measured. In fact, for a given Q peak, the θ distribution reflects the angular momentum of the corresponding valence-neutron state. So Jones and company measured Q distributions at various fixed values of θ. From those Q spectra, they were able to calculate the differential scattering cross sections, as functions of θ, for neutron transfer to each of the four observed valence-neutron states.
The team then compared those differential cross sections with what one would see if the valence state were some particular pure quantum state nlj. (As in atomic-spectroscopy notation, n is the principal quantum number that specifies the radial dependence of the state’s wavefunction; l is the orbital angular momentum, alphabetically denoted; and the subscript j is the valence neutron’s total angular momentum.) From those comparisons, the team determined the best-fit quantum numbers for the four observed valence states. Shown in figure 4, they are indeed just what the shell model predicts for a single extra neutron orbiting the closed shells of a perfectly spherical 132Sn core.

Figure 4. Valence states of the extra tin-133 neutron. For each of the valence levels observed in the Oak Ridge experiment, schematically shown above the doubly magic 132Sn core, the best-fit quantum state is given (left) together with its spectroscopic factor S (right), a measure of spectral purity. In the spectroscopic notation, p and f denote, respectively, orbital angular momenta 1 and 3. If the best-fit state is pure, with no admixture of other quantum states due to core excitations, S = 1.
(Adapted from
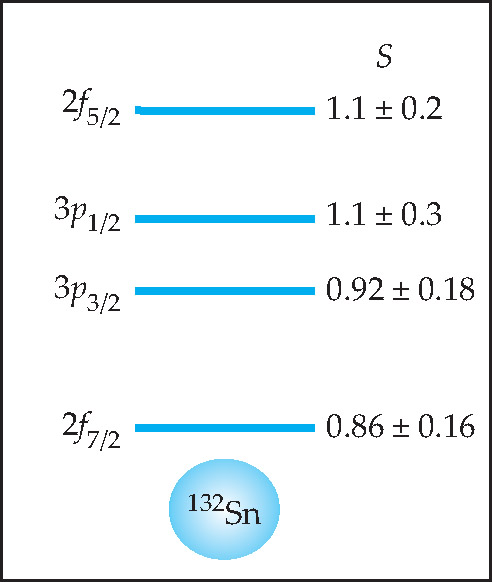
But testing the doubly magic character of that core requires more than just determining the quantum numbers that fit the valence states best. One must also assess the spectral purity of those states. If the valence states are not well isolated from the spherical core, they will mix with core states and become fragmented superpositions of several pure nlj states.
A widely used measure of spectral purity is the so-called spectroscopic factor S. If the valence state contains only a single nlj state then S = 1. Decreasing S means increasing fragmentation. Next to each valence state in figure 4 is its spectroscopic factor calculated by the experimenters from the fits between the measured cross sections and what’s expected for the pure states. All four turn out to be consistent with S = 1. (S greater than 1 has no physical meaning.)
“That’s even better than one gets for 208 Pb, the much studied paradigm of doubly magic nuclei,” says Nazarewicz. “So 132Sn may be the most magic of them all.” For the third and fourth valence-neutron states of 208 Pb, by comparison, Pb-target experiments find that S is no bigger than 0.6.
What about doubly magic light nuclei like 4He and 16O? The shell model, which approximates the effects of all the other nucleons on any one nucleon by a mean-field potential, gets better with increasing mass number. The structure of the very lightest nuclei is more appropriately a few-body problem that can be addressed by ab initio calculations.
With regard to the r process, attention is now turning to 78 Ni. As shown in figure 1, it sits at the only other magic-number intersection adjacent to the r-process region. With an excess of 16 neutrons, 78 Ni has a half-life of 0.1 s, 400 times shorter than that of 132Sn. “But that shouldn’t stop the experimenters,” says Nazarewicz. “In fact, they’ve already started.”
References
1. K. L. Jones et al., Nature 465, 454 (2010). https://doi.org/10.1038/nature09048
2. P. Cottle, Nature 465, 430 (2010). https://doi.org/10.1038/465430a

