Supersolid behavior in helium coincides with enhanced shear modulus

Solid helium is an odd and elusive material. At pressures less than 25 atmospheres, it doesn’t even exist. The interaction of the helium atoms is so weak, and their quantum zero-point motion so great, that helium can remain liquid down to absolute zero. Decades ago it was predicted that atomic vacancies, inherent in the solid due to zero-point energy, could condense into a single quantum state and allow the solid to flow without friction. The predicted phase was termed “supersolid,” in parallel with superfluidity and superconductivity.

In 2004, Moses Chan, of the Pennsylvania State University, and his then-student Eun-Seong Kim published results strongly suggesting that they had observed supersolidity. ¹ (See Physics Today, April 2004, page 21 , and November 2004, page 23 .) The researchers confined solid helium in a cylindrical cell, which was suspended by a torsion rod. From the resonant frequency at which the cell twisted back and forth, they deduced the helium’s moment of inertia. When they cooled the cell below 200 mK, a small fraction of the helium appeared to have decoupled from the rest. It wasn’t contributing to the moment of inertia and seemed to be flowing with respect to the twisting cell.

Several groups since then have performed their own versions of Chan’s torsion-oscillator experiment and have made new, mysterious observations. Cornell University’s John Reppy and his student Ann Sophie Rittner found that the amount of apparent mass decoupling is much greater in rapidly cooled samples, which are expected to have more structural defects. ² And Chan and colleagues have recently observed that the transition temperature is lower in isotopically purified helium, ³ with 1 part per billion helium-3, than in standard samples, which have about 300 ppb ³He.

Those results suggest that supersolidity—or whatever was observed in the torsion-oscillator experiments—is not an intrinsic property of the solid ⁴He crystal but depends strongly on disorder and impurities. Consistent with that interpretation, theoretical calculations found that the vacancies in a single crystal of pure ⁴He don’t form a superfluid after all, ⁴ but superflow could still be possible in glassy regions, near grain boundaries, or along the lines of dislocations.

Evidence that the solid helium might not be flowing at all came in 2006 from the University of Alberta’s John Beamish and his student James Day. ⁵ They looked for linear flow driven by a pressure difference—and found none. But late last year, Chan and colleagues measured a small peak in solid helium’s specific heat near the onset of the apparent mass decoupling, ⁶ evidence of a phase transition to a new state of matter, supersolid or not.

Now, Day and Beamish have measured solid helium’s shear modulus ⁷ —the force per unit area required to distort the solid by a certain amount. “Rigidity is the property that defines a solid,” explains Beamish, “and it’s affected by dislocations in ways that we think we understand. It really seemed to me that people should look at it directly.”

Day and Beamish found that at the same temperature that the moment of inertia drops in the torsion-oscillator experiments, the shear modulus changes too. Says Chan, “This is one of the most important breakthroughs on solid helium since the original discovery.”

Shear joy

The usual way of finding a solid’s shear modulus is by measuring shear sound waves, whose speed is a function of the material’s shear modulus and density. When the density is known, that method works well. But in a material with a supersolid component, part of the mass may decouple from the rest, and the effective density may vary. A change in the sound speed could come from a change in the shear modulus, the onset of supersolidity, or both.

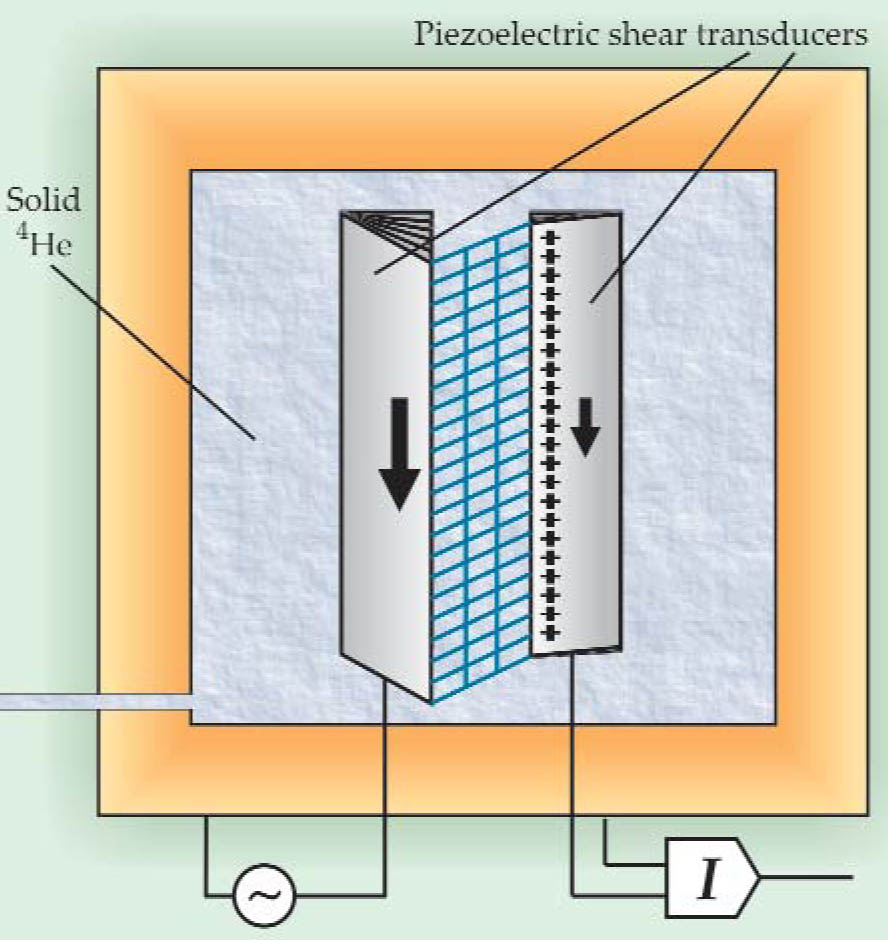
To resolve the ambiguity, Day and Beamish built a new apparatus, shown schematically in figure 1, for measuring the shear modulus directly. They sandwiched a layer of solid helium between two piezoelectric crystals and applied an oscillating voltage to one of them. The stress transferred to the other crystal generated an output current, from which the researchers deduced the shear modulus of the helium layer.

Says Beamish, “I certainly hoped to see a change in the shear modulus in the temperature range below 200 mK, but I wouldn’t have bet on the magnitude or the sign.” In fact, as the temperature was lowered, he saw the shear modulus increase. The helium got stiffer, and to a surprising degree. Whereas the torsion-oscillator experiments typically revealed a change on the order of 1% in the helium’s moment of inertia, the shear modulus often increased by 10% or more.

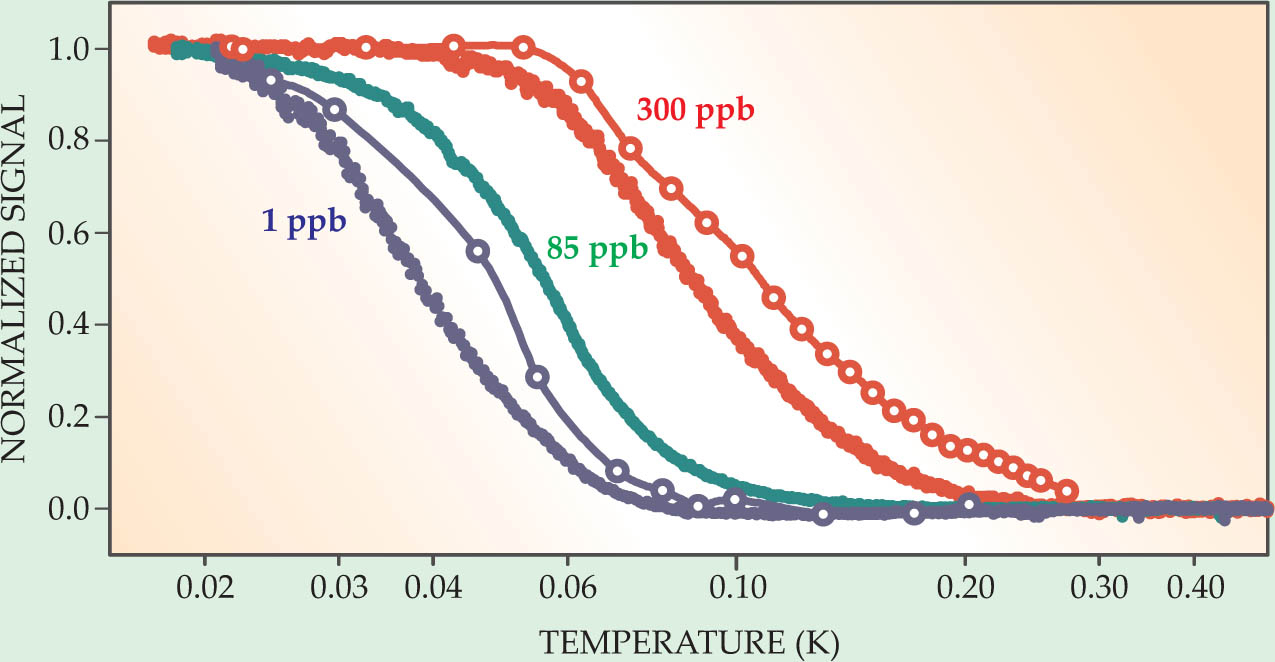
Another surprise was just how closely changes in the shear modulus paralleled those in the moment of inertia. The temperature dependence was almost identical between the two types of experiment, as was the dependence on the ³He concentration (see figure 2). Coaxing the helium into a better-quality crystal through annealing, which nearly eliminated the moment-of-inertia change in some torsion-oscillator experiments, also reduced the change in shear modulus. The two effects seemed related. But how?

Dislocation, dislocation, dislocation

Day and Beamish favor an explanation that involves the interaction of ³He impurities with structural defects in their ⁴He crystal, particularly line defects, or dislocations. Beamish explains, “We can understand our results generally with the sort of dislocation behavior already understood in metals. But it isn’t completely clear yet how quantum mechanics is affecting the dislocations’ behavior, nor how dislocation motion might affect a supersolid state.”

In metals and other classical solids, the crystal lattice is stretched on one side of an edge dislocation (the termination of an atomic plane) and compressed on the other. That makes the sites surrounding the dislocation ideal spots for impurities. Impurity atoms that are bigger or smaller than the lattice atoms can lower the energy of a dislocation by fitting into the stretched or compressed region of the lattice. There is thus an energy of attraction between impurities and dislocations. Because dislocations normally move more easily than impurity atoms, the binding between them makes the dislocations less mobile. That pinning of the dislocations, in turn, makes the whole crystal more difficult to deform and its shear modulus greater. (For more about dislocations and impurities in metals and their impact on the manufacture of cutlery, see the Quick Study by Louis Bloomfield, Physics Today, May 2007, page 88 .)

Usually, different isotopes of the same element are all the same size—determined by the electronic structure—so isotopic impurities do not interact with dislocations. But very light elements such as helium are different: The lattice spacing—the effective atomic size—is significantly affected by the atoms’ quantum zero-point vibrations. Because the lighter ³He vibrates more than the heavier ⁴He, ³He is effectively about 2% bigger. That difference suffices for ³He atoms to be weakly attracted to dislocations in a ⁴He crystal, with a binding energy of about 0.6 K. Only a fraction of the ³He atoms need to bind to the dislocations to pin them in place. When the ³He concentration is higher, that fraction is lower, and the pinning transition can occur at a higher temperature.

What such dislocation pinning has to do with the apparent mass decoupling in the torsion-oscillator experiments is much less clear. Day and Beamish think perhaps supersolidity requires long-range phase coherence that is disrupted by mobile dislocations but not by dislocations frozen in place by ³He. Boris Svistunov (University of Massachusetts Amherst) and colleagues have proposed a related mechanism, in which superflow occurs along the dislocation lines themselves. An isolated one-dimensional dislocation does not support superflow at any finite temperature. But at low temperature, the dislocations could cross-link into a 3D network, which would both stiffen the crystal and allow superflow.

Whatever mechanism underlies solid helium’s odd behavior must also be able to explain Kim and Chan’s original experiment, which looked at helium trapped in the tiny pores of Vycor glass. Dislocations and disorder operate very differently in such a confined geometry, yet Kim and Chan observed similar amounts of apparent decoupling in Vycor and in the bulk. “We clearly do not yet have the whole story about what is happening in solid helium,” says Robert Hallock of the University of Massachusetts Amherst. “But the work of Day and Beamish is very relevant and important. Any understanding of what is happening in the solid must also be able to deal with their new measurements.”