Short-range spin waves may underlie high-temperature superconductivity

Since the discovery nearly 25 years ago of high-temperature superconductivity in a family of copper oxides, or cuprates, theorists and experimentalists alike have struggled to understand the mechanism behind the phenomenon. Is it something akin to conventional superconductivity, in which a weak attractive interaction holds the fermionic electrons together in bosonic bound states, which then condense into a superfluid? Or might some fundamentally new theory be required?

In a conventional superconductor, as explained by the Bardeen-Cooper-Schrieffer (BCS) theory, the electrons are held together in pairs by an interaction mediated by lattice phonons. Each electron couples to the spectrum of phonons through its Coulomb attraction to the positively charged nuclei; the result is an attractive interaction between electrons. The attraction is very weak, but as Leon Cooper originally showed, even a weak attraction suffices to create electronic bound states.

The BCS theory is not specific to a phonon-mediated interaction; other excitations can also serve as the “pairing glue.” But until recently, phonons were the only candidate known to be present in all of the superconducting cuprates, and yet a phonon-mediated interaction didn’t seem to do the trick. Now, researchers led by Bernhard Keimer (Max Planck Institute for Solid State Research) have produced compelling evidence in favor of a different possibility: electron pairing mediated by paramagnons, or short-range spin waves superposed on the copper spins’ underlying antiferromagnetic order. ¹

Seeking spin waves

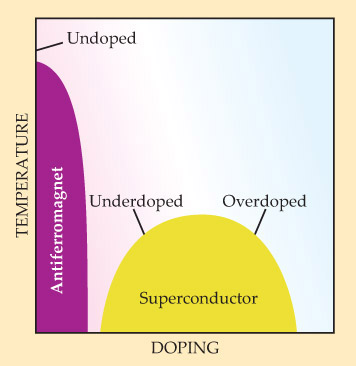
As the schematic phase diagram in figure 1 shows, the superconducting cuprates exist on a continuum with a family of nonsuperconducting antiferromagnetic insulators. “Doping” refers to the concentration of charge carriers (electrons or holes); undoped and weakly doped cuprates have long-range antiferromagnetic order at low temperatures. In the superconducting cuprates, that long-range order breaks down, but some short-range correlations remain. Nuclear magnetic resonance studies have revealed that optimally doped cuprates—those that exhibit superconductivity at the highest temperatures—have spin correlations on the scale of about three unit cells. ² In some underdoped cuprates—those that are still superconducting but have lower critical temperatures due to lower doping—the correlations extend over six unit cells.

That short-range order can still support spin waves, but the waves are damped, like the ripple formed by a pebble dropped into a puddle of viscous mud. Ordinary, long-range spin waves are called magnons; the damped ones are known as paramagnons. It’s been known experimentally that electrons do couple to spin waves, and theoretically that if paramagnons exist over a wide enough range of energies, they can produce the necessary attractive interaction to induce superconductivity. ³ But sufficiently strong paramagnons had never been seen over the full range of superconducting cuprates.

Keimer has been engaged in a long-standing program to study magnetic excitations in cuprates via inelastic neutron scattering. That technique has detected a broad paramagnon spectrum in some of the strongly underdoped cuprates—those closest to the antiferromagnetic parent compounds—but only very low-energy excitations (30–70 meV) for the rest of the cuprates, insufficient by an order of magnitude or more to produce superconductivity. Some researchers have inferred from the neutron-scattering results that paramagnons can’t mediate cuprate superconductivity. But Keimer notes that because of limitations in the technique—small scattering cross sections and low beam intensities—the inability to see the intense paramagnons doesn’t mean they’re not there.

X-ray vision

While working on an unrelated system (orbital excitations in titanium oxides), Keimer became aware of recent rapid improvements made by Giacomo Ghiringhelli and Lucio Braicovich in a different technique, called resonant inelastic x-ray scattering (RIXS). ⁴ Ghiringhelli and Braicovich’s latest success used RIXS to study the magnon spectrum in undoped, antiferromagnetic cuprates. They joined forces with Keimer and his colleague Mathieu Le Tacon to see if the technique would work on superconducting cuprates as well.

The researchers looked at a range of cuprates—from undoped to overdoped—over a range of scattering angles to access excitations of different energies. In every superconducting sample they tried, they found a paramagnon spectrum similar in intensity to the magnon spectrum of the undoped cuprates. Figure 2 shows the spectra for the two extremes in the range of compounds studied.

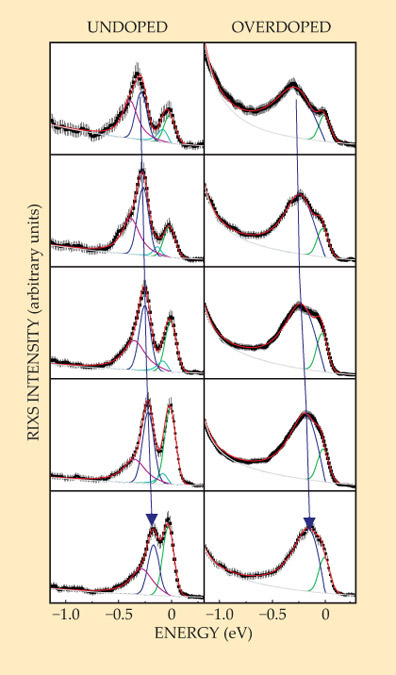
In fact, says Keimer, “The magnetic excitations were much more intense than we had expected.” The biggest challenge, he explains, was in accessing sufficiently low-energy excitations in order to get some overlap with the neutron-scattering experiments, to demonstrate that both techniques were detecting the same excitations. With a clever choice of scattering geometry to minimize the elastic-scattering background, they managed to obtain a few points of overlap.

Critical temperatures

Keimer and colleagues’ results show that paramagnons exist across the entire range of cuprates, and with sufficient intensity to mediate superconductivity. That addresses the main source of doubt about paramagnons as the cuprates’ pairing glue. But there’s still much that remains unclear. A full understanding of cuprate superconductivity will require, among other things, a theory to connect the observed paramagnon spectra to the observed critical temperatures.

The best existing theoretical methods applicable to magnetically mediated superconductivity are still very crude. Keimer and colleagues applied one method—called Eliashberg strong-coupling theory, which is also applicable to conventional superconductors—to their overdoped cuprate and found that it reproduced the critical temperature to within a factor of 2. That’s a similar level of accuracy to what Eliashberg theory can achieve for conventional superconductors.

As for further experimental proof that paramagnons not only exist but also mediate cuprate superconductivity, Keimer explains, “The materials chemistry of the cuprates and the physics of strongly correlated electrons are very complex. It would be naive to expect a single smoking-gun experiment. However, the evidence has been accumulating steadily over the past two decades.