Shaped light waves can pass through opaque material
DOI: 10.1063/1.2982110
Matter can block light, and thus appear opaque, by absorbing the light or by scattering it. Opaque materials with low absorptivity—milk, white paint, and some living tissue, for example—are generally well described as random arrangements of scattering particles. When light hits them, much of it is reflected, but some of it is transmitted as a diffuse blur with random speckles due to constructive and destructive interference. The thicker the material, the less light is transmitted.
Since the 1980s, theorists have used random matrix theory to study the scattering of both photons and electrons. 1 They found that for the transmission matrix of a randomly scattering material, each of the eigenvalues is either nearly zero or nearly one. That is, any wave entering a scattering material can be represented as a sum of modes, some of which are entirely transmitted and some of which are entirely reflected. Thicker samples have more reflecting (or closed) channels and fewer transmitting (or open) ones. In theory, then, as long as not all of the channels are closed, it should be possible to create an incoming wave that couples into only the open channels, not the closed ones.
Now, Allard Mosk of the University of Twente in the Netherlands and his recently graduated student Ivo Vellekoop have demonstrated a method for shaping a light wave that greatly increases the transmitted intensity. 2 And their results are in quantitative agreement with the predictions of random matrix theory. Says John Pendry of Imperial College London, “I find the results very exciting. The open–closed channel theorem is one of the most important results on disordered systems. As far as I am aware, it has not been verified experimentally before.”
Coming into focus
As Mosk explains, “The project began in 2005, when we realized that the diffusion of light waves in nontransparent materials is not a thermodynamically irreversible process. So there should be a way to reverse it.” In 2007 he and Vellekoop successfully focused a portion of the light transmitted through a layer of white paint onto a predefined target point.
3
(See Physics Today, October 2007, page 26

Figure 1. Focusing light through an opaque material. (a) When a plane light wave is shone on a strongly scattering sample, such as a layer of white paint, a diffuse speckle pattern is transmitted, and the rest of the light is reflected. The thicker the sample, the lower the transmitted intensity. (b) When the wavefront is shaped by adjusting the relative phases of different parts of the beam, the constructive interference is optimized at a target point. The diffuse speckle pattern is still present.
(Adapted from ref. 3.)
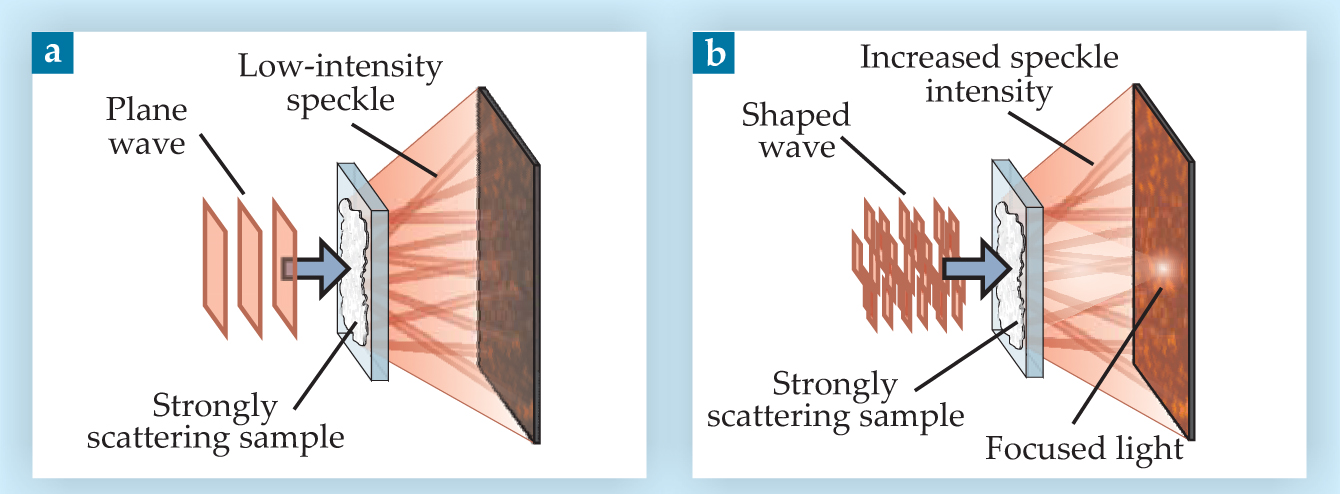
The researchers reflected a coherent laser beam off a spatial light modulator, an array of liquid-crystal pixels. With an applied electric field, they could tune the refractive index of each pixel, which in turn adjusted the phase of that part of the beam. They then passed the beam through a microscope objective so that the light reflected off each pixel was reduced to a diffraction-limited spot, a few hundred nanometers square. Their unshaped wave gave the expected random speckle pattern.
To shape the wave, they scanned the pixel phases one at a time and tracked the effect on the transmitted intensity at the target point. For each pixel, the phase that gave the maximum target intensity was the one for which the contribution of that segment of the beam was in phase with the diffuse background. In principle, when all the pixels are set to their optimum phases, the contributions at the target point from all the segments of the beam should be in phase with each other, so the intensity at the target point would be maximized.
But in the 2007 experiments, the waves weren’t controlled nearly as well as they might have been, for two reasons. First, slight temperature changes in the laboratory caused parts of the apparatus to drift over the course of the few minutes it took to create a shaped wave—a shift of the scattering sample by half a wavelength with respect to the laser beam would destroy the entire optimization. Second, spatial light modulators exhibit a phenomenon called cross modulation, whereby tuning the phase of a segment of a beam also changes its amplitude. So although the intensity at the target spot increased by a factor of 1000 for some of the samples, that increase was less than 10% of what might have been achieved with a perfect optimization.
Shedding more light
Since last year, Vellekoop, Mosk, and their colleague Elbert van Putten have developed a way to correct for cross modulation. 4 By working with the pixels of the spatial light modulator in groups of four rather than individually, they can tune a segment’s amplitude and phase independently. As a result, they can adjust its phase while keeping its amplitude constant. That improvement, along with upgrades to other parts of the apparatus, allows for much more control over the shaped wave.
The new experiments offer an answer to an important question about the behavior of random scatterers: When light is focused onto the target point, does it diminish the intensity of the reflected light rather than the diffuse transmitted light? In other words, is the focusing algorithm also a method for increasing the total transmission—for coupling more light into the open channels that are predicted by theory?
As figure 2 shows, it is. Compared with the unshaped wave, the shaped wave transmits more light not only to the target point, as expected, but also to the rest of the speckle area. For the shaped wave shown, the target intensity increased by a factor of about 750, and the total transmission increased from 0.23 to 0.31.

Figure 2. Transmitted intensity distributions for (a) an unshaped wave and (b) a shaped wave. (c) The same distributions summed in the vertical direction. The shaped wave (solid blue curve) produces not only a high-intensity focus but also a brighter speckle pattern than the unshaped wave (dashed brown curve).
(Adapted from ref. 2.)
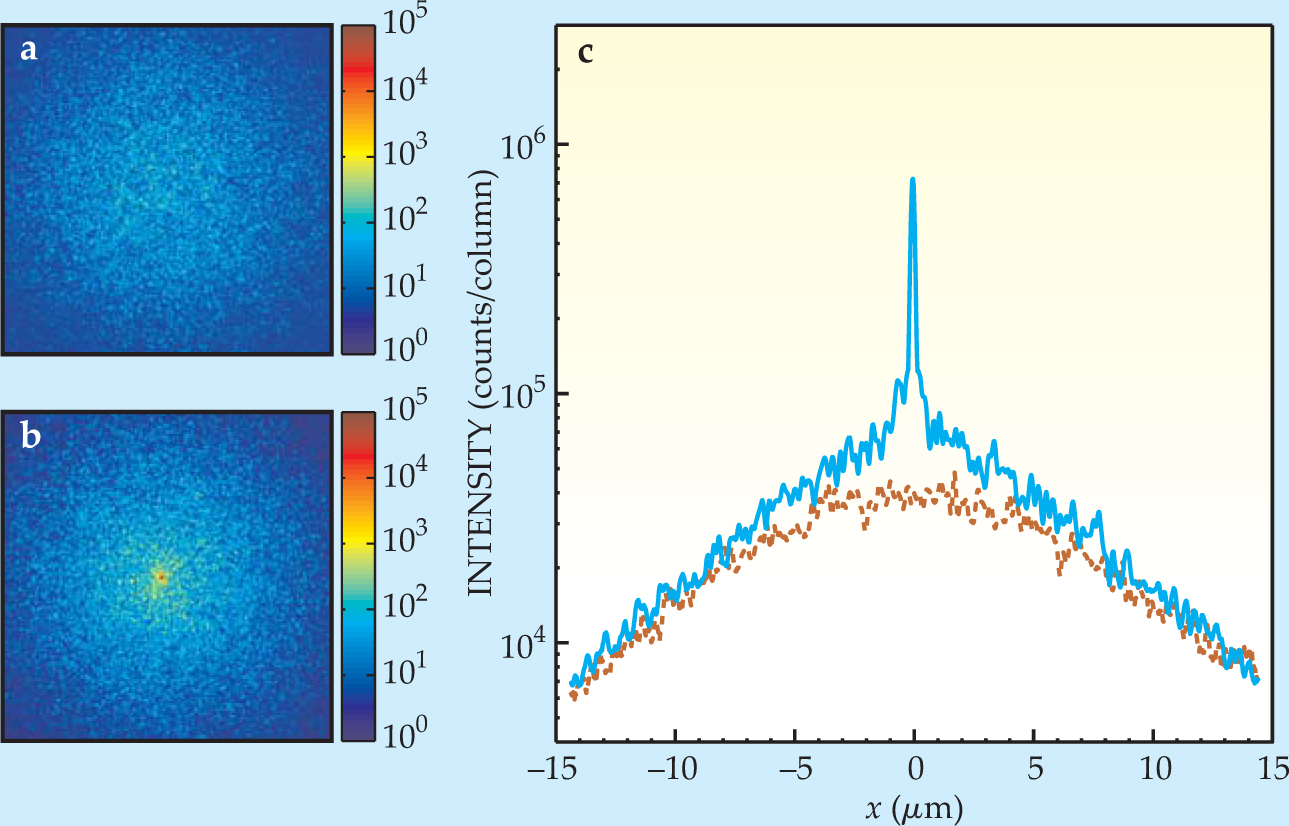
To make a quantitative comparison between their results and the theory, Vellekoop and Mosk represented their shaped wave as the sum of a perfectly shaped part and a random part. Their so-called degree of control is the intensity of the perfectly shaped part divided by the total intensity of the incident beam. By definition, the intensity at the target point is proportional to the degree of control. Theory predicts that the total transmitted intensity is a linear function of the degree of control, so the target intensity and the total transmitted intensity should be linearly related to each other.
The total transmission of the unshaped wave depends on many properties of the sample, including its thickness. But according to random matrix theory, the transmitted fraction of the perfectly shaped wave is always
Vellekoop and Mosk’s experimental limitations prevent them from creating a perfectly shaped wave—the highest degree of control they’ve been able to achieve is about 0.33. But they do see an excellent linear fit between the total transmission and the degree of control, and extrapolating from their data to a perfectly controlled wave gives a transmitted fraction of 0.68 ± 0.07, in agreement with the theoretical value. Says Carlo Beenakker of Leiden University, “The experiment is really a striking demonstration of the existence of open channels.”
References
1. O. N. Dorokhov, Solid State Commun. 51, 381 (1984); https://doi.org/SSCOA4
10.1016/0038-1098(84)90117-0
J. B. Pendry, A. MacKinnon, P. J. Roberts, Proc. R. Soc. A 437, 67 (1992). https://doi.org/PRLAAZ10.1098/rspa.1992.0047 2. I. M. Vellekoop, A. P. Mosk, Phys. Rev. Lett. (in press).
3. I. M. Vellekoop, A. P. Mosk, Opt. Lett. 32, 2309 (2007). https://doi.org/OPLEDP
10.1364/OL.32.002309 4. E. G. van Putten, I. M. Vellekoop, A. P. Mosk, Appl. Opt. 47, 2076 (2008). https://doi.org/APOPAI
10.1364/AO.47.002076
More about the Authors
Johanna L. Miller. jmiller@aip.org




