Sensitive cantilevers detect the persistent currents in normal-metal rings

In 1983 Markus Büttiker, Yoseph Imry, and Rolf Landauer made a bold prediction: Persistent currents, long thought to be the exclusive province of superconductors, should also exist in a normal-metal ring—provided the ring is threaded with a magnetic flux. ¹ Controversial at the time, the prediction could hardly have been more counterintuitive. Currents induced in a resistive wire usually decay in less than a picosecond, due to thermal fluctuations and the scattering of electrons with defects, phonons, and each other. The inelastic electron-electron and electron-phonon scattering mechanisms, moreover, alter the quantum states of the electrons and rob them of their phase memory.

If the ring is small enough and cold enough, though—on the order of a micron at temperatures under a kelvin, say—the electrons’ phase coherence length may exceed the ring’s circumference as inelastic scattering becomes increasingly rare. Electrons still scatter elastically from thousands of atomic defects, grain boundaries, and other static impurities during each orbit around the circuit. But those collisions, the theorists realized, do not destroy the phase information contained in the wavefunction; they merely shift its phase, even as they increase the resistance.

The magnetic field threading the ring breaks time-reversal symmetry, so the persistent current can flow in a specific direction, either clockwise or counterclockwise. Measuring that current is a daunting challenge. On the order of a nanoamp according to theory, the current flows only within a closed ring and thus cannot be measured with a conventional ammeter. Only in the induced magnetic moment µ is the current revealed. And the moment from an individual ring is remarkably faint—roughly 100 bohr magnetons, the sensitivity limit of the best magnetic detectors.

Despite the difficulty, separate groups led by Laurent Lévy (then at Bell Labs) and Richard Webb (then at IBM) confirmed the 1983 prediction nearly a decade later using superconducting quantum interference devices. ^{2 , 3} Lévy’s group enhanced the minuscule magnetic signal of a single copper ring by sensing the response of an array of 10 million of them. Webb’s group measured the SQUID’s response to single, individual rings. But in both experiments the measured currents were larger than expected—in the IBM case, between 30 and 150 times larger (see Physics Today, April 1992, page 17 ). The discrepancies between experiment and theory (and indeed between different experiments, mostly SQUID-based) prompted a still-ongoing effort to fully understand the phenomenon. ⁴

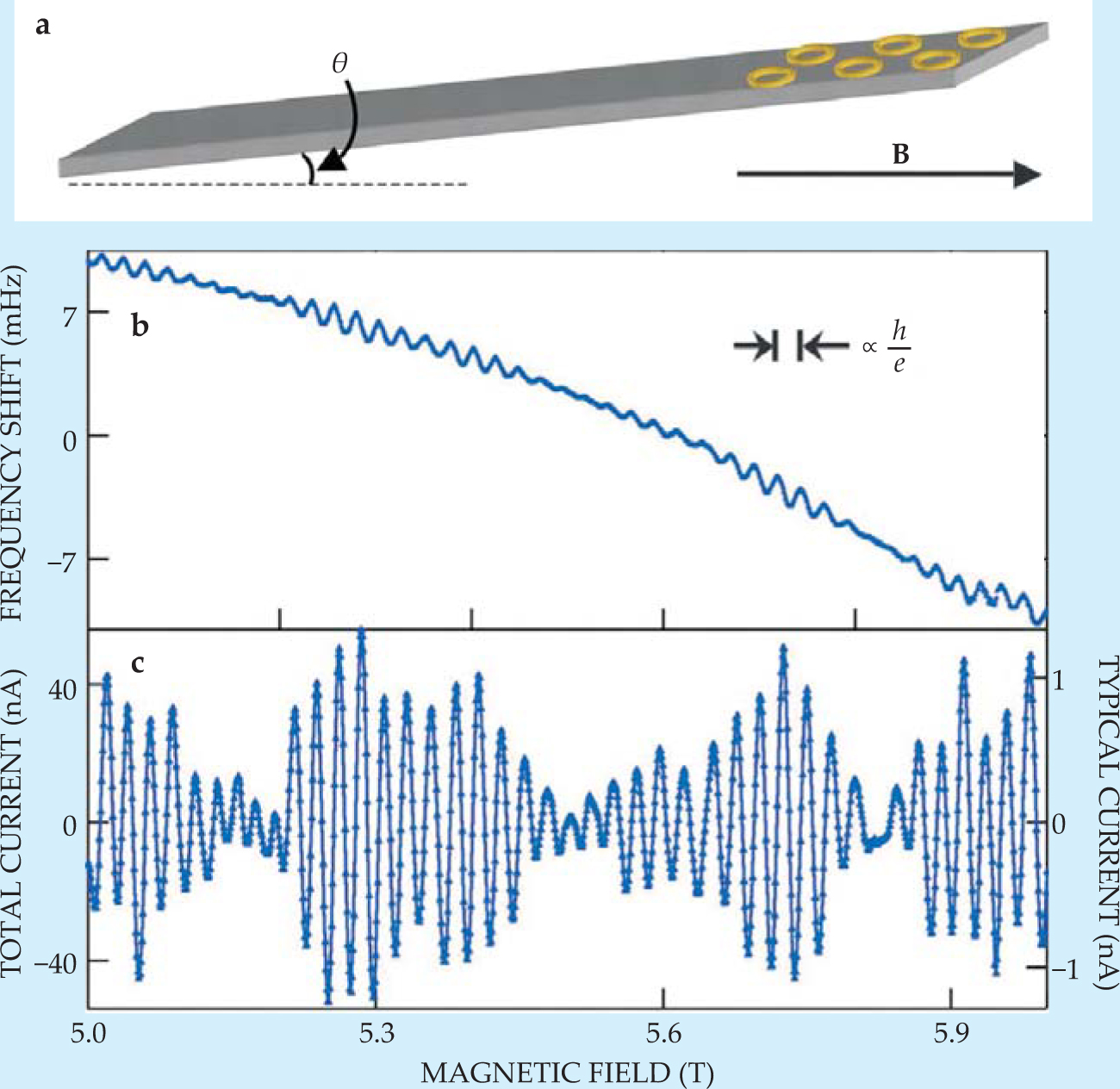
Jack Harris and colleagues from Yale University and the Free University of Berlin have now developed an alternative measurement scheme, ⁵ as outlined in figure 1. Theirs is based on a micro-mechanical approach: In essence, the team deposited aluminum rings on a cantilever whose vibration frequency can be precisely monitored. In the presence of an applied magnetic field B, each ring’s current produces on the cantilever a torque τ = µ × B, recorded as a shift in the cantilever’s resonance frequency of vibration. From that frequency shift, they could deduce the persistent current.

The allure of the technique, says Büttiker, lies in its sensitivity—more than two orders of magnitude greater than SQUID-based approaches. “This method may become to persistent currents what the telescope was to astronomy.”

Aharonov–Bohm

Because phase coherence and quantum interference are behind its existence, a metal ring’s persistent current can exhibit an Aharonov-Bohm effect. For a magnetic flux ø threading the ring, the electron wavefunction acquires a phase proportional to øe/h around the circumference of the ring, where e is the electron’s charge and h is Planck’s constant. The electron wavefunction must be single-valued going around the ring, so the phase added by the magnetic flux is compensated for by the electron’s motion to make the total phase an integer multiple of 2π. That motion, which corresponds to the persistent current, is consequently periodic in the applied magnetic field with a period given by the addition of one flux quantum h/e through the ring.

The beauty of those Aharonov-Bohm oscillations is that they provide a clear signature so that the persistent current stands out from stray electromagnetic signals induced by magnetic impurities such as iron. Unfortunately, in addition to their low signal-to-noise ratios, SQUIDs perform best in low magnetic fields, a regime that gives researchers few oscillations to measure and complicates the subtraction of background signals unrelated to persistent current.

Still, SQUID-based research has steadily narrowed the gap between theory and experiment in the past decade. Earlier this year Kathryn Moler and her Stanford University colleagues ameliorated those problems by modifying a SQUID to scan across 33 individual gold rings, one at a time. That approach helped distinguish spurious signals and led to measurements of the current’s amplitude in close agreement with theory, although the rings’ small magnetic moments still required hours of statistical averaging. ⁶

The micromechanical approach extends the measurements to high magnetic fields, where the signal is easier to detect. The extension also makes it possible to probe the behavior of superconductors well above the magnetic field that turns them normal. The researchers observed as many as 450 oscillations in Al rings over a 5.5-T range. (Figure 1(c) shows just a fraction of the data.) The aperiodic component of the current arises from the fact that the applied field doesn’t just thread the ring; it also penetrates the metal, which leads to different phase shifts for electron paths that enclose different areas. The phase randomization, Harris argues, alters the effective disorder potential felt by electrons in the ring.

The flexibility of the approach is also an advantage. The Yale group measured persistent currents induced in a single ring and arrays of them over a much broader range of temperatures and magnetic fields than had been previously possible. “I have to say,” he admits, “when we started this project, I didn’t understand the theory well enough to know what to look for in most of those quantities. So the problem was not so much the case of finding the needle in the haystack as cataloging the entire haystack and then combing through it to see if it made sense.” Inspiration for the technique came from Harris’s earlier graduate work in the late 1990s designing cantilevers to sense the tiny forces created by two-dimensional electron gases.

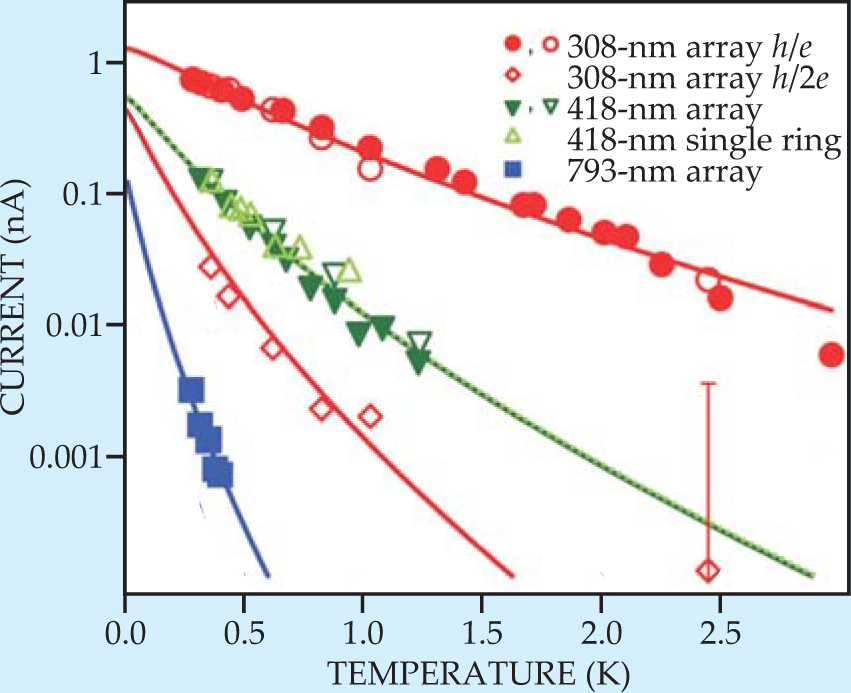
The new results, ⁵ shown in figure 2, illustrate a nearly perfect agreement with a model of noninteracting electrons, a model that requires just one fitting parameter—the electron diffusion constant of Al. The direction of the persistent current in each ring depends on details of its defects and the number of electrons and thus varies randomly from ring to ring. The total signal measured from an array of rings scales as the square root of the number of rings, reflecting the randomness.

Interacting electrons

It’s perhaps no surprise that the current’s properties depend just on temperature and resistivity of the metal in a regime where the independent-electron approximation reigns. But the Yale group’s quantitative account offers a proof of principle for the technique and sets the stage for work at low magnetic fields, where richer physics lies. There, as Imry puts it, “electron—electron interactions turn on and all hell breaks loose.”

The interactions and screening effects are manifest in a component of the current whose period is half the magnetic flux quantum, or h/2e. The component’s origin lies in a two-particle version of coherent backscattering. To every zigzagged path an electron might take as it circles the ring there corresponds a precise, time-reversed path through the same scattering centers. Those equivalent pairs of trajectories reinforce each other constructively, which adds the factor of two to the phase shift. Because the effect is a delicate interference involving a sum over relatively few coherent terms, it’s easily upset by any significant magnetic field in the metal.

Lévy’s group detected the h/2e signal in its early 1990 study on copper, ² though with a magnitude at least five times the theoretical value and a sign that indicated attractive electron interactions. That’s a surprise for a metal not found to superconduct even at temperatures as low as 10 µK. Last year Imry and collaborators proposed an intriguing explanation: ⁷ Copper would be a superconductor, they argue, were it not for the influence of tiny part-per-million (or less) levels of magnetic impurities. The impurities break electron pairs and suppress the phase transition but hardly affect the persistent current, which is determined on a larger energy scale.

Once the torque magnetometer is optimized for low fields, Harris plans to address that idea experimentally. He also wants to explore circuits more complicated than the simple metal ring. One can envision, for example, engineering a ring coupled to a quantum dot or grain of superconducting material; that configuration would set normal and persistent currents in competition with each other.