Relativistic effects seen at everyday distances and speeds

In George Gamow’s popular account of special relativity, his title character, Mr. Tompkins, dreams of a “Wonderland” in which passing bicyclists appear flattened by length contraction. Gamow achieved the effect in his fiction by setting the speed of light at a mere 30 miles per hour. Recently, researchers at NIST in Boulder, Colorado, also made relativity seem more commonplace, but not by resorting to a literary artifice. Instead, they used accurate clocks to measure the much smaller but very real relativistic effects that occur at everyday time and distance scales.

The NIST team has developed the most precise optical clocks in the world, based on the optical frequency of an electron transition in a single aluminum ion trapped nearly at rest (see the article by James C. Bergquist, Steven R. Jefferts, and David J. Wineland in Physics Today, March 2001, page 37) ). In the recent experiment, the clocks could detect the minuscule relativistic effects that arise when the ion in one clock oscillates with an average speed of just 10 meters per second (about 22 mi/hr) relative to the stationary ion in a second clock, or when the elevation of one clock changes by as little as 33 cm. ¹

The first of those effects is the equivalent of special relativity’s twin paradox. The oscillating ion plays the role of the traveler, whose clock runs more slowly than that of its look-alike at home. The second effect is the gravitational frequency shift experienced by clocks at different points in a gravitational potential.

The experiment is an excellent demonstration of the high performance reached by NIST’s optical clocks, states Christophe Salomon of the École Normale Supérieure in Paris. The more accurate of the two clocks used in the experiment was unveiled last February ² and has a systematic frequency uncertainty of 8.6 × 10^-18. By contrast, the current SI standard for time is a cesiumatom fountain clock, operating at microwave frequencies, with an accuracy on the order of 10^-16.

The NIST group is certainly not claiming to have made the most precise test of relativity; many other techniques at various scales have put the theory through its paces. James Chin-Wen Chou, lead author on the new NIST paper, points out that among laboratory measurements, Mössbauer spectroscopy and atom interferometry have greater sensitivities to gravitational effects than atomic clocks, although the two clocks have the distinction that they can be located in separate laboratories. Holger Müller of the University of California, Berkeley, finds a philosophical appeal to the optical-clock measurements. Unlike the other two techniques, which involve extremely high oscillation frequencies, he says, “the new work operates on everyday scales with a clock you can use to measure heartbeats.’

To see the relativistic effects, Chou and his colleagues required not only highly sensitive clocks but also a low-noise 75-meter-long optical fiber to transfer the signal from a clock in one laboratory to a reference clock located down the hall.

Ion clocks

To achieve high accuracy in the clocks used in the recent demonstration, NIST researchers needed a way to efficiently cool an ²⁷Al ion and to detect its optical transition. For those tasks, they exploited a logic operation developed for quantum information science (see Physics Today, October 2005, page 24) ). The technique pairs the Al ion with a fluorescing magnesium-25 ion, which is used to monitor whether a clock laser is on resonance with Al’s narrow ¹ S₀ ↔ ³ P ₀ line (8 mHz). As Chou explains it, if the clock laser has not excited the Al ion, a second probe laser will be able to induce a collective motion between the Al and Mg ions. The kinetic energy can be translated into a change in the internal state of the Mg ion, turning off its fluorescence signal. If, however, the pump laser has succeeded in exciting the ²⁷Al, the probe laser will fail to induce collective motion and the Mg ion will continue to fluoresce. The fluorescence then signals that the clock laser is tuned to the atomic transition.

In the older clock used as a reference in the recent experiment, the logic ion was beryllium-9 rather than ²⁵ Mg. The cooling and detection work better when the logic ion has a mass that’s closer to that of the Al ion because then the two ions more equally share the energy of collective motion.

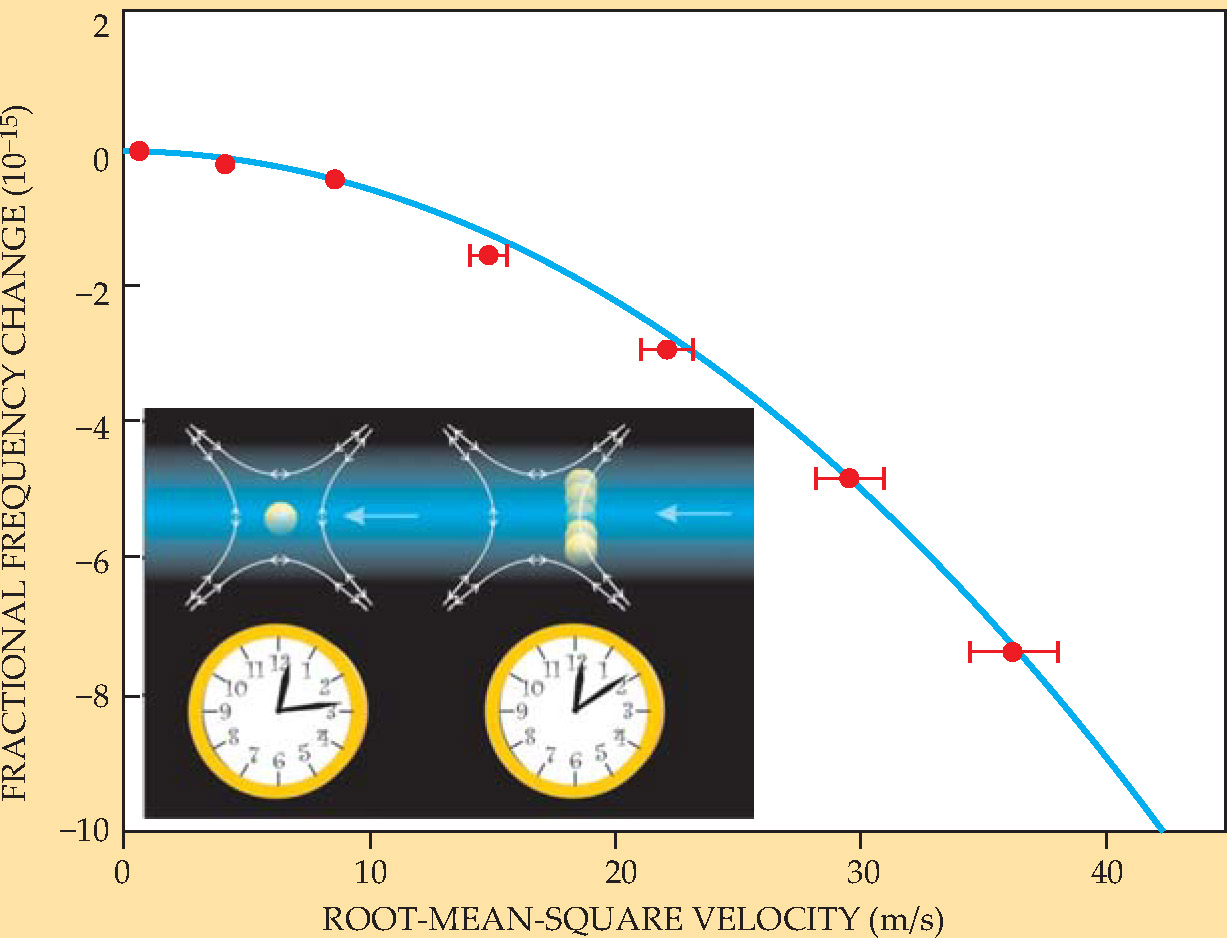
To measure time dilation due to motion, Chou and his colleagues nudge the Al ion in the Al-Mg clock a bit away from the ion trap’s center so that it experiences harmonic motion, while the Al in the Al-Be clock remains essentially at rest. As seen in figure 1, the faster the oscillation of the traveler ion, the greater is the downward shift of its clock frequency.

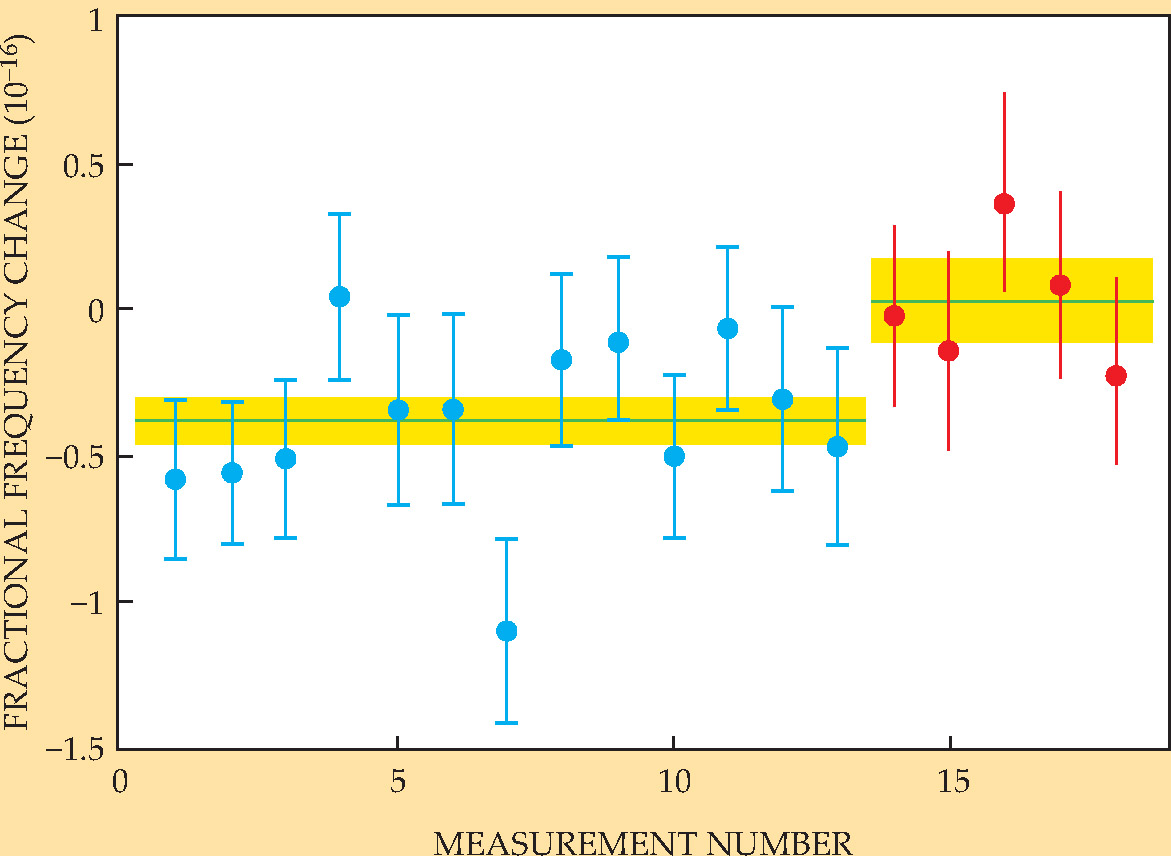
To determine the gravitational frequency shift that makes the two clocks beat at different rates, the NIST group put the Al-Mg clock on a table whose height could be altered with a jack. It was connected to an Al-Be clock that remained at one elevation in another lab. The Al-Mg clock started out 17 cm below the other clock and then was raised by a total of 33 cm. Figure 2 shows the shift in the clocks’ frequency difference.

Geodesic applications

Salomon notes that the NIST experiment has important implications for geodesy, the mapping of Earth’s gravitational potential and changes to it. A succession of satellite missions — CHAMP, GRACE, and GOCE—have been mapping Earth’s potential (see Physics Today, February 2003, page 18 ). Satellites can now determine the geoid, the hypothetical surface of constant gravitational potential, to about 1 cm but that’s averaged over areas hundreds of kilometers on a side. Optical clocks could complement those measurements with readings at distributed points on Earth’s surface if clock designers reach their goal of one part in 10¹⁸ accuracy and if researchers can find a way to accurately compare clocks at widely separated locations. MIT’s Daniel Kleppner has pointed out some challenges that arise when clocks become so accurate (see Physics Today, March 2006, page 10 ).

Rather than comparing distant ground-based clocks to one another, one might compare them to a reference clock on board a satellite. Researchers plan to launch a laser-cooled cesium clock and a hydrogen maser into space in a European Space Agency program, Atomic Clock Ensemble in Space (ACES). One of its missions is to provide high-precision space-to-ground and ground-to-ground comparisons of clock frequencies.

The clocks aboard ACES will also test relativity and measure the constancy of fundamental constants. The most accurate test of the gravitational redshift to date has been the 1980 measurement by Robert Vessot and colleagues using a hydrogen maser launched to an altitude of 20 000 km on a rocket. Recently, Müller and two colleagues reinterpreted ³ a decades-old atom interferometry experiment, initially performed as an accurate determination of the acceleration of gravity, in terms of a very precise measurement of the relativistic gravitational frequency shift (see Physics Today, April 2010, page 19 ). A Paris-based group has questioned that reinterpretation. ⁴ At issue is essentially whether the gravitational redshift can be measured independently of the acceleration of free fall.