Rapid data exchange helps keep a secret for 24 hours

Cryptography’s most familiar use is perhaps the sending of coded messages: Alice wants to communicate some information to her distant confidant Bob. She worries that her message might be intercepted by an eavesdropper, so she encrypts it in a way that only Bob can decipher. A related task involves digital signatures: Alice wants to prove to Bob that her message came from her rather than an impostor.

There’s a broad range of complementary cryptographic tasks, though, in which Alice and Bob seek to guard against dishonesty not from intervening third parties but from each other. Examples include silent auctions and secret ballots: Participants want to ensure not only that their own bids or votes are kept private but also that the outcome isn’t being unfairly manipulated by any other participant.

To develop algorithms to perform those tasks, cryptographers use a building block called bit commitment. Alice chooses a secret bit (a 1 or 0) to be revealed later. Bob wants to guarantee that Alice can’t change her mind in the meantime, and Alice wants to make sure Bob has no information about which bit she chose until she reveals it.

Anthony Martin, Hugo Zbinden, and their colleagues at the University of Geneva have now capitalized on the impossibility of faster-than-light signaling to implement a scheme that preserved the secrecy of one bit for 24 hours. ¹ Because the experiment was carried out entirely within the city of Geneva, with no parties more than a few kilometers apart, the commitment required a complex protocol involving billions of rounds of information exchange. The achievement was due in part to recent theoretical work ² proving that the protocol is fundamentally secure—and in fact, that it could feasibly be extended to commitment times of a year or more.

Quantum insecurity

In most cryptographic applications, tasks—including both message encryption and bit commitment—are carried out using protocols that rely on so-called computational security: To crack the code, a would-be cheater or eavesdropper must solve a problem, such as finding the prime factors of a large number, that would take billions of years on any present-day computer. When the stakes are especially high, however, it would be useful to have a protocol that’s secure against any adversary, even one with access to unlimited computing power. (See the article by Daniel Gottesman and Hoi-Kwong Lo, Physics Today, November 2000, page 22 .)

For message encryption, that perfect security can be achieved with quantum key distribution, in which Alice and Bob use a series of entangled qubits to derive a cryptographic key that only the two of them can possibly know. Because measuring a quantum state changes it, any eavesdropping attempt can be instantly detected, and Alice and Bob can discard the compromised key. But any hope that quantum theory could provide similar security for bit commitment was dashed by two 1997 papers proving that all quantum bit-commitment schemes can be cracked. ³

It’s possible, however, to achieve secure bit commitment if Alice works with a trusted partner, Amy, who can be isolated from Alice during part of the protocol. Alice and Amy need first to agree on the bit d that they wish to commit and a random integer a between 1 and some number N. Bob chooses a random integer b, also between 1 and N. With Alice and Amy cut off from each other, Bob shares b with Alice, who replies with (a + bd) modulo N. Alice and Amy remain isolated until it’s time to reveal the secret bit, at which point Amy tells Bob a, from which Bob can deduce d.

Bob has no way to cheat this system—that is, to learn the value of d before Amy reveals a. All he has from Alice is a random number, and he can’t possibly know whether it truly corresponds to a or to a + b mod N. Alice and Amy, on the other hand, might be able to cheat. Suppose they agree at the outset that d = 0. Alice answers Bob with a, as she should, but she and Amy want to convince Bob later that they’d actually chosen d = 1. They can do that if Amy gives Bob (a − b) mod N and pretends that that was the original a. Amy can’t perform that calculation because she doesn’t know b. But she can guess, and 1/N of the time she’ll guess correctly and get away with it. That risk of cheating can be made acceptably small simply by making N sufficiently large.

Practical cryptography doesn’t offer any mechanism of preventing agents from communicating with each other. But the laws of special relativity do: If Amy reveals a before any light-speed signal can reach her with information about Alice and Bob’s initial exchange, then she can have no information about b, just as if she and Alice had been isolated.

Round and round

With Alice and Amy both located on Earth, they can be at most 40 light-milliseconds apart. To achieve bit commitment for longer than that, it’s necessary to extend the above scheme into a more complicated, multiround protocol. Instead of revealing a right away, for example, Amy could exchange some information with Bob’s nearby partner Brian, so that Brian doesn’t learn the value of a right away but he’ll be able to deduce it later.

In his 1999 proposal for relativistic bit commitment, ⁴ Adrian Kent suggested that Amy treat the binary representation of a as a series of new bits d_i to be committed, each using new random numbers a_i (shared in advance between Alice and Amy) and b_i (supplied by Brian). Then Alice can either reveal the a_i to Bob or commit their binary representations d_ij to him with random numbers a_ij, and so on. In principle, that sequence of rapid exchanges—one between Alice and Bob, the next between Amy and Brian—could be carried out indefinitely. But in practice, because the amount of data exchanged grows exponentially with time, it would quickly overwhelm the capacity of any realistic signaling channel.

In 2015 Zbinden and his group teamed up with theorist Stephanie Wehner and her colleagues to design and implement a different protocol, shown in the figure. ⁵ In it, Alice and Amy need to prearrange just one random number a_i per round in advance of the planned commitment. Bob and Brian also need one number b_i per round.

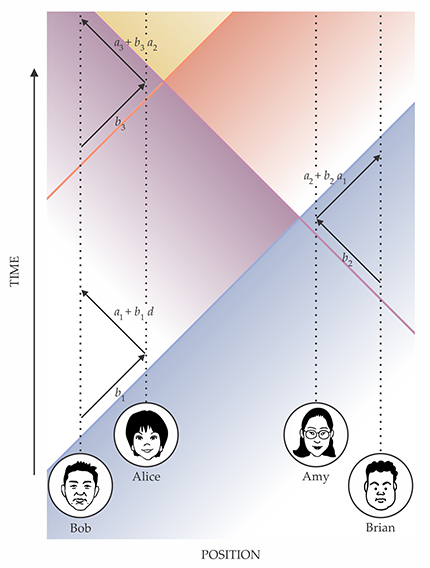
The first round proceeds as before: Bob sends Alice the value of b₁, and she replies with a₁ + b₁d. In each subsequent round, Brian (or Bob) sends b_i to Amy (or Alice), who replies with a_i + b_ia_{i − 1}. At the end of the m-round protocol, Alice or Amy reveals a_m and d, from which Bob and Brian can verify that d is in fact the bit that was chosen in the beginning. (Here, multiplication and addition are performed in the so-called finite field of N elements, and they behave slightly differently from the ordinary real-number operations. Subtraction and division are still well defined, however, so Bob and Brian can carry out all of Alice and Amy’s calculations in reverse at the end of the protocol.)

As before, Bob and Brian can’t cheat. The numbers they receive from Alice and Amy are all randomly distributed between 1 and N, and none of them carries any useful information. And as before, Alice and Amy can try to cheat by guessing one of the b_i with probability 1/N. But can they do better? Rigorously proving the protocol’s security is more complicated than guessing cheating strategies and calculating their success rate—it’s necessary to account for all possible strategies, even those that haven’t been discovered.

Rather than calculating Alice and Amy’s cheating probability exactly, Wehner and colleagues derived an upper bound on it. Unfortunately, that bound grew as a double-exponential function of the number of rounds m, although none of the cheating strategies they identified had success rates nearly as large as their bound. Still, to guarantee that the cheating rate was kept to a reasonable level, the researchers had to limit m to approximately log log N.

In their initial implementation of the protocol, ⁵ Zbinden and colleagues chose an N of 2⁵¹²—that is, each random number comprised a string of 512 bits. To keep the cheating rate below 10⁻⁹, they were limited to just six rounds of exchange. With Alice and Bob in Geneva and Amy and Brian 437 light-microseconds away in Bern, they thus sustained the bit commitment for 2 ms.

Better than expected

As it turned out, the protocol was actually much more secure than initially thought. Two groups of theorists, one led by Serge Fehr and the other by Anthony Leverrier, soon proved that the cheating probability doesn’t scale double-exponentially with m, but linearly. ² With that realization, longer bit-commitment times immediately became possible, with reasonable security over not just 6 rounds, but billions. Martin, Zbinden, and colleagues now had the luxury of using smaller random numbers (strings of 128 bits rather than 512) and shorter distances between agents, all within the city of Geneva.

The experimenters placed the computers representing Alice and Bob in the same room and connected them with a 1 m optical link. Just 23 light-microseconds away, Amy and Brian had a similar setup. With so little separation between the pairs, timing was critical to satisfying the relativistic constraints. To account for the nonzero duration of each round and to allow a small tolerance for error, the researchers chose to begin each round of the protocol 17 µs after the previous one. Each pair was synchronized to a GPS receiver that kept time with 150 ns accuracy.

All told, the 24-hour commitment of a single bit required 162 GB worth of random numbers; a year-long commitment would require 59 TB. That amount could be reduced by moving the agents farther apart and lengthening each round of the protocol. For example, if Alice and Bob were 10 000 km away from Amy and Brian, a year-long commitment could be achieved with just 81 GB.