Quantum memory for light takes a leap forward
DOI: 10.1063/1.3480062
Photons are good carriers of quantum information. They’re relatively easy to entangle, in amplitude and phase as well as in polarization, and they can traverse long distances quickly. But quantum communication protocols often involve storing qubits and saving them for later—to be measured jointly with other qubits, for example—and no method yet exists for storing light for arbitrarily long times without unacceptably corrupting its quantum state.
Beginning in 1999 several research groups have used electromagnetically induced transparency to slow and stop light (see Physics Today, March 2001, page 17
One measure of a light-catching scheme’s performance is its efficiency, defined as the intensity ratio of the retrieved signal to the input signal; efficiency normally represents an upper bound on the amount of quantum information that can be preserved. The standing efficiency record for a quantum memory—one that preserves any quantum information at all — is 15%. Now Matthew Sellars, of the Australian National University in Canberra, and colleagues have developed a quantum memory that’s up to 69% efficient. 2 Crossing the 50% efficiency threshold is significant because it makes it possible for more than half of the quantum information to be preserved—no eavesdropper could cobble together a better copy of the signal than the one retrieved from the memory. Furthermore, Sellars and company’s storage medium is a solid, not a gas, so it may be more easily incorporated into devices.
Broadening horizons
The Canberra group used a variant of a technique called controlled reversible inhomogeneous broadening, 3 first reported in 2006, to store light in an ensemble of rare-earth ions (praseodymium in their experiment) doped into a transparent crystal (yttrium orthosilicate, or Y2SiO5). Their procedure is shown in figure 1. An electric-field gradient Stark-shifts the energy levels of the dopant ions so that the energy of a particular electronic transition is different in different parts of the crystal. That is, the transition is inhomogeneously broadened.

Figure 1. Quantum memory in a praseodymium-doped transparent crystal. (a) An inhomogeneous electric field E shifts the Pr ions’ electronic transition energies ħw via the Stark effect. (b) An incident light pulse excites each ion into a coherent superposition of ground and excited states whose phase (symbolized by the rotation of the ion itself) evolves at a rate proportional to the transition energy. (c) Flipping the sign of E reverses the distribution of Stark shifts. (d) When the ions are all in phase, a pulse is emitted. The ratio of the output intensity to the input intensity is the memory’s efficiency.
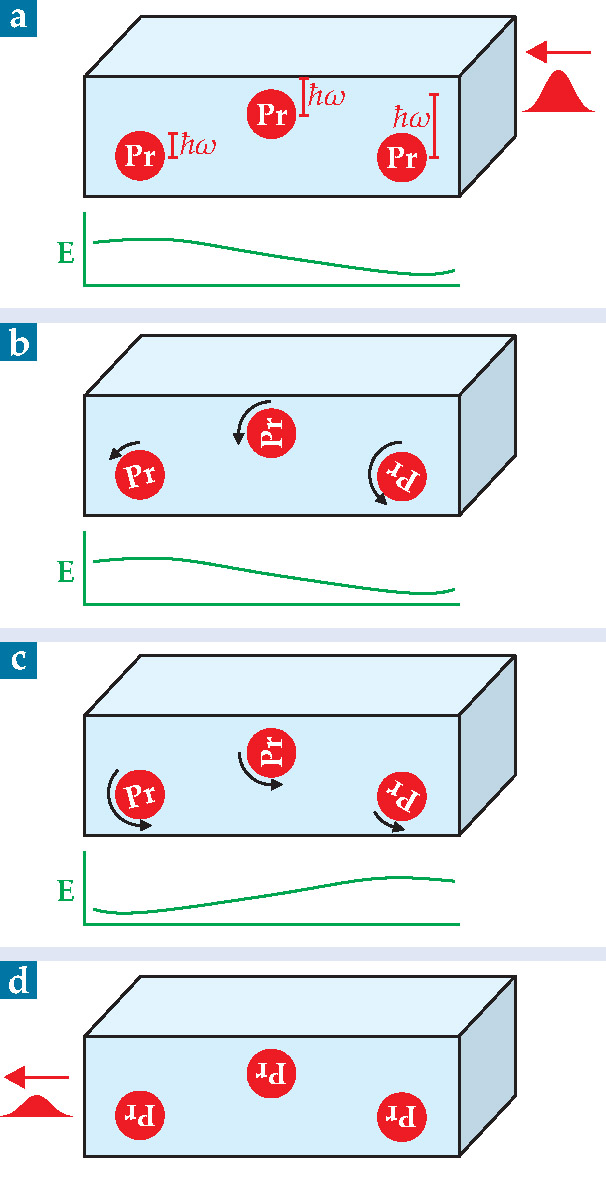
A light pulse, whose frequency spectrum lies within the broadened transition, excites the ions into coherent superpositions of their ground and excited states. The phase of the superposition evolves at a rate proportional to the transition energy, which is different in each ion, so before long, the ions are out of phase. Flipping the sign of the electric field reverses the distribution of Stark shifts. The ions come back into phase, at which point their spontaneous emission pathways interfere constructively in the forward direction, and a pulse is emitted.
Unfortunately, crystal inhomogeneities—slight differences in stress or orientation, for example—induce a natural inhomogeneous broadening much larger than the desired range of Stark shifts. To create a sharper transition, the researchers used spectral hole burning, as shown in figure 2: A frequency-stabilized laser beam optically pumps atoms into a different hyperfine state if their transition energies fall just above or just below a particular narrow range. The sharp absorption peak that remains can then be broadened by the electric field.
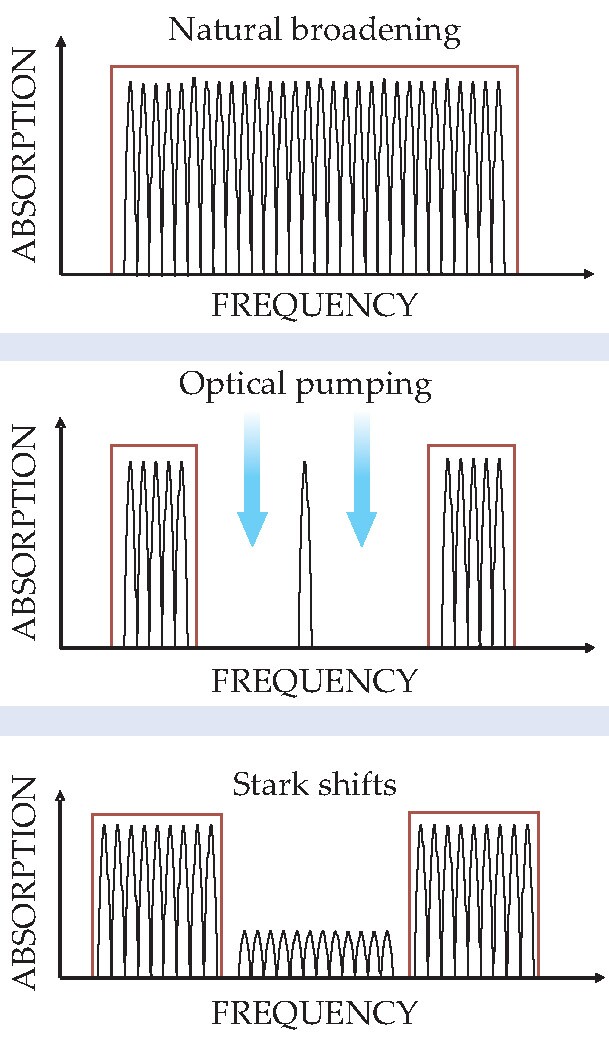
Figure 2. Spectral hole burning creates a narrow absorption feature out of a naturally broadened line by optically pumping some atoms into an out-of-the-way hyperfine state. The peak is then broadened by an applied electric field.
(Adapted from
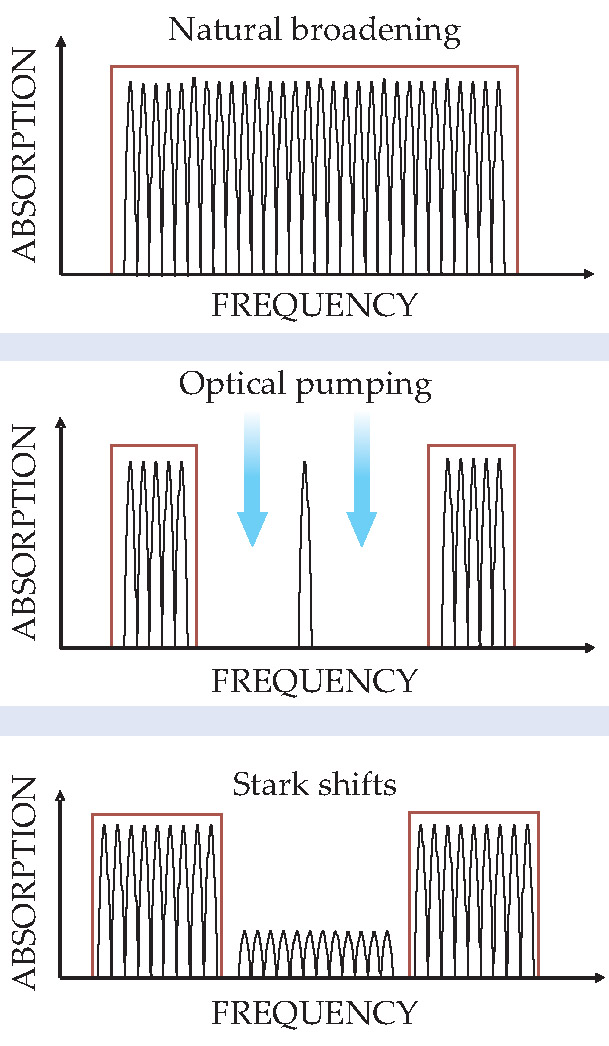
For hole burning to succeed, the optical pumping beams need to access the entire crystal. But to store the input pulse with high efficiency, the crystal needs to be optically thick—otherwise, much of the input light will pass straight through it and be lost. Sellars and company’s innovation was to use a long, thin, lightly doped crystal, with the hole-burning light applied to the side and the input pulse to the end. In that way, the researchers were able to create a strong, sharp absorbing feature with little background on either side. “I suspect this would be the sharpest spectral filter ever demonstrated,” says Sellars. “We hope it might have other applications.”
Memory test
The memory was 69% efficient for storage times of 1.3 µs and 45% for 2.6 µs; the efficiency declined exponentially from there. But efficiency is just a measure of the output pulse’s intensity; it says nothing about the information the pulse contains. To evaluate that—and to gauge how faithfully the outputs reproduced the inputs—a separate measure is needed.
Rather than characterizing any one pulse both before and after storage in the memory, the researchers measured several thousand input pulses and several thousand output pulses, and they compared the variance of each group. Measuring a pulse involved beating it against a local oscillator pulse derived from the same laser but offset by 2.5 MHz. By taking many measurements while slowly scanning the phase between the data pulse and the local oscillator, the researchers obtained a quantity that represented the variances in both amplitude and phase.
The result of interest is the variance of the outputs minus the variance of the inputs, or the variance added by storage in the memory, and there are two important thresholds to which to compare it. Performance beyond the classical limit is the defining characteristic of a quantum memory: The output is a better copy of the input than could be achieved by a perfect classical measurement and reconstruction. More stringent is the so-called no-cloning limit, which marks the point beyond which no eavesdropper could have a better copy of the input pulse.
A memory with efficiency η exceeds the classical limit if its added variance, in units of the vacuum variance, is less than 2η, and it beats the no-cloning limit if its variance is less than 2η − 1. Those are sufficient but not necessary conditions, but the latter shows that it’s difficult to exceed the no-cloning limit with an efficiency of less than 50%—that is, to convey more than half of the quantum information without more than half of the light.
Those benchmark values don’t depend on input intensity, so an intense pulse with a lot of classical noise must clear the same low threshold as a faint pulse with little classical noise. When the researchers measured the added variance for pulses of four different intensities—average photon numbers of 4, 30, 500, and 19 000—they found that the 4-photon and 30-photon pulses both exceeded the no-cloning limit, the 500-photon pulses beat the classical limit but not the no-cloning limit, and the 19 000-photon pulses exceeded neither limit.
The researchers looked exclusively at Gaussian pulses, but they note that more complicated signals could also be stored—as long as the signal’s Fourier transform fits within the memory’s bandwidth and as long as its duration doesn’t exceed the memory’s storage time.
Repeater performance
Quantum memory for light is relevant to long-distance quantum communication through its role in a so-called quantum repeater. A classical repeater—a device that receives a signal and rebroadcasts it at higher power—has no quantum equivalent, since an unknown quantum state can’t be amplified (see the Quick Study by William Wootters and Wojciech Zurek in Physics Today, February 2009, page 76
If Alice and Bob want to exchange one bit of information through a quantum channel, they must each possess one of a pair of entangled qubits. But when qubits are transmitted to widely separated locations, the probability of preserving their entanglement decreases exponentially with distance. If Alice is in Albany, New York, and Bob is in Bakersfield, California, direct distribution of entangled qubits is essentially impossible.
A quantum repeater divides a long transmission channel into shorter segments—with the help, say, of Charlene in Chicago, Illinois, and Denise in Denver, Colorado. (In practice, many more nodes would be required—at least one every 150 km or so.) Alice and Charlene transmit qubits to each other until one entangled pair gets through. If necessary, they can use an entanglement purification scheme 4 to convert collections of noisily entangled qubits into one well-entangled pair. Charlene and Denise do the same, as do Denise and Bob. Charlene then makes a joint measurement on her two qubits, which has the effect of entangling Alice’s qubit with one of Denise’s. Denise then does likewise, thus giving Alice and Bob their desired entangled pair.
For that protocol to work, Charlene needs to store the qubits she receives from Alice and Denise long enough to establish entanglement across both segments. That is, she needs a quantum memory with a storage time of milliseconds or, ideally, seconds. Combining Sellars and company’s high efficiency with longer storage times is one of the next big challenges for quantum-memory researchers.
Sellars plans to address the challenge by transferring the quantum information from the rare-earth ions’ electronic states to their nuclear spin states. That improvement, he says, could increase the storage time to seconds or even hours. He and his colleagues are also working on growing doped crystals with more perfect lattices and narrower rare-earth spectral lines. “If we can reduce the natural inhomogeneous broadening in the crystal,” he says, “then we won’t have to use spectral hole burning. The memory operation would then be incredibly simple.”
References
1. B. Julsgaard et al., Nature 432, 482 (2004). https://doi.org/10.1038/nature03064
2. M. P. Hedges et al., Nature 465, 1052 (2010). https://doi.org/10.1038/nature09081
3. B. Kraus et al., Phys. Rev. A 73, 020302–R (2006); https://doi.org/10.1103/PhysRevA.73.020302
A. L. Alexander et al., Phys. Rev. Lett. 96, 043602 (2006). https://doi.org/10.1103/PhysRevLett.96.0436024. See, for example, J. -W. Pan et al., Nature 410, 1067 (2001). https://doi.org/10.1038/35074041
5. W. Tittel et al., Laser Photonics Rev. 4, 244 (2010). https://doi.org/10.1002/lpor.200810056

