Precision spectroscopy reveals a highly forbidden electronic transition in helium

Willis Lamb’s 1947 measurement of the tiny energy splitting between the 2S and 2P states of atomic hydrogen largely spawned the development of quantum electrodynamics (QED). Ever since, precision spectroscopy of simple atomic systems has been used to test the theory and refine our understanding of it. In the latest contribution to that effort, ¹ researchers led by Wim Vassen (Vrije University Amsterdam) have resolved—to a precision of 1.5 kHz, or 8 parts in 10¹²—an exceedingly weak IR transition between the triplet and singlet metastable states of atomic helium, 2 ³S₁ and 2 ¹S₀. So highly forbidden is the excitation, which violates both spin and parity selection rules, that it has never before been seen, much less measured to high precision.

Individually, the states are energy levels of different species of helium—orthohelium, in which electron spins are parallel, and parahelium, in which they’re antiparallel. The distinct emission spectra of the two spin arrangements were noticed in the late 19th century but not understood until Werner Heisenberg explained them in 1926.

A photon’s electric field does not interact directly with the electron spin. Nor can it connect two states of the same parity. Yet for the doubly forbidden excitation to occur, one of the orthohelium spins must flip to form parahelium. Were it not for the photon’s magnetic field, which couples to an electron’s magnetic moment, such flips would be impossible. In fact, the magnetic interactions and relativistic corrections to the Schrödinger equation show that the triplet-to-singlet excitation is allowed as a magnetic dipole transition, but with a probability 14 orders of magnitude weaker than that of the familiar electric dipole transition in He from 2 ³S to 2 ³P.

Why go to the trouble of probing it? With the S states’ large electron density at the He nucleus, their energy levels are more sensitive to two-electron QED and to nuclear-size effects. In addition, because the singlet state 2 ¹S₀ is long-lived (20 ms), it has a natural linewidth of just 8 Hz, 200 000 times as narrow as 2 ³P.

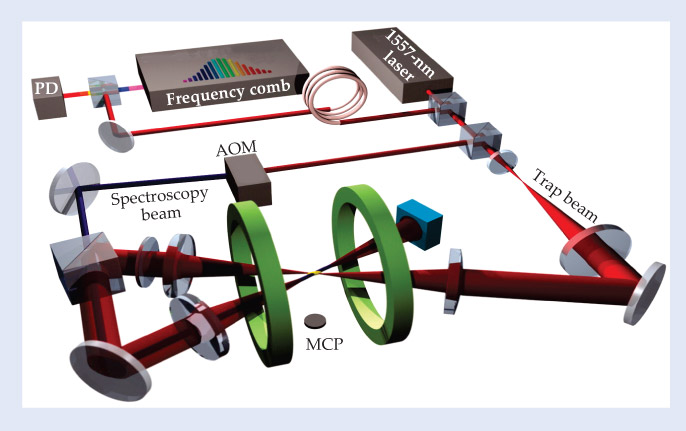
To measure so weak a transition requires either high laser power or long interaction times. Whereas earlier spectroscopy of He exploited atomic beams or gas discharge cells, in which atoms and light intersect for mere nanoseconds, the Amsterdam experiment combines optical trapping and frequency comb technology. ² The trap brings a few million He atoms to a near standstill, effectively eliminating Doppler broadening, and allows them to interact with excitation light for up to 6 s; the comb, in turn, is locked to a rubidium clock and provides a rock-solid laser-frequency calibration (see figure 1).

Load, cool, and drop

The Amsterdam team can load ³He, ⁴He, or both into the optical trap. To create a Bose–Einstein condensate of ⁴He, the researchers evaporatively cool the gas, which draws off the highest-energy atoms and leaves the rest to reequilibrate through elastic collisions. Fermionic ³He atoms are harder to tame: Because of Pauli exclusion, they stop colliding at millikelvin temperatures. Five years ago Vassen’s group succeeded in creating the first ³He degenerate Fermi gas by further cooling the ³He atoms “sympathetically” through collisions with ⁴He atoms to reach microkelvin temperatures. An appropriately tuned RF pulse can then spring the bosons, but not the fermions, from the trap. The following year the group used the experimental setup to study the pattern of bunching or antibunching that occurs when the bosons or fermions fall onto a surface (see PHYSICS TODAY, March 2007, page 18 ).

The advantage of using degenerate or near-degenerate gases in spectroscopy is the high density of atoms that can be packed into a tight laser focus. The disadvantage is the possible interactions between them. Surprisingly, though, Vassen and colleagues found that any frequency shifts associated with atomic collisions are so small as to fall within their error bars.

Another advantageous feature of the experiment, using either isotope of He, is that the same IR (1557-nm) laser used to trap the triplet-state atoms can also be used to excite them. Fortuitously, whereas the triplet-state atoms feel an attractive trapping potential from the light, the singlet-state atoms feel a repulsive one. So when the spectroscopy beam is resonant with the atomic transition, any atoms excited to the singlet state are subsequently expelled from the trap.

After a few seconds, the trapping and spectroscopy beams are turned off and the remaining atoms fall onto a microchannel plate that counts them. The researchers ran hundreds of experiments to resolve the transition frequency for the different isotopes. One such experiment is depicted in figure 2, which shows a Gaussian fit to the dip observed in the percentage of triplet-state ⁴He atoms as the applied laser frequency was stepped up or down through the resonance.

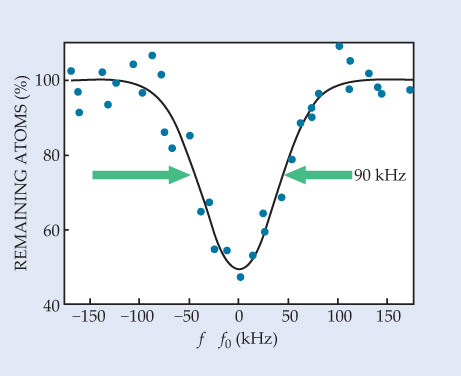
The group used an off-the-shelf IR laser. Its linewidth, combined with a contribution from the feedback loop between the laser and frequency comb, largely accounts for the broad 90-kHz width of the result. The linewidth for state-of-the-art lasers at national metrology labs is on the order of a hertz, so orders-of-magnitude improvement may be possible, at least in principle.

Nonetheless, the fitted plots, once corrected for systematic frequency shifts, such as the Zeeman effect caused by Earth’s magnetic field, revealed the transition frequency to a precision 1000 times better than that of current QED calculations. Reassuringly, experiment and theory agree, as nearly everyone expected. But the two approaches closely interact; improved experimental values may inspire better calculation methods to explain them.

Spectroscopy can even transcend atomic physics. So precise are the electronic measurements that even tiny variations in the size and shape of the nucleus influence them. Equally precise QED calculations for He are required to interpret that influence. Fortunately, the main problem of calculating the effect of emission and reabsorption of a virtual photon has recently been solved. ³ By measuring the isotope shift—the slightly different transition energies between triplet and singlet states in ³He and ⁴He—the Amsterdam group was able to deduce a competitive value for the charge radius of the ³He nucleus (1.961 ± 0.004 fm).

And that, down the road, may come in handy for calculating an improved value for the Lamb shift in He.