Polariton condensates show their nonequilibrium side

Can a Bose–Einstein condensate exist at room temperature? If it’s made of atoms, not by a long shot. To coax a gas of bosonic atoms to pile up in their quantum ground state, researchers must cool the gas to within a few millionths of a degree of absolute zero.

More accessible condensates can be made by replacing the atoms with polaritons: light–matter quasiparticles that form when photons in an optical cavity couple to electronic excitations in a solid. Because the quasiparticles have such low effective masses, their quantum effects set in much more easily.

Polariton condensates form at standard cryogenic temperatures—around 4 K, the temperature of liquid helium—and under some circumstances, even at room temperature. ¹ The warmer conditions make it easier to study the physics of quantum condensation and to pursue potential technological applications (see the article by David Snoke and Jonathan Keeling, Physics Today, October 2017, page 54 ).

But polariton condensates aren’t quite the same as atomic Bose–Einstein condensates. Unlike stable atoms, polaritons persist for only as long as their constituent photons remain trapped in the cavity—usually on the order of a few picoseconds. To keep a polariton condensate from decaying away to nothing, researchers have to keep repumping it with fresh photons. As a result, the condensate never thermally equilibrates; at best, it approaches a steady state.

Does it matter whether a polariton condensate is populated with new photons or old ones? Jacqueline Bloch (University of Paris–Saclay), Léonie Canet (Grenoble Alpes University), and colleagues have now shown that it does: Because of its nonequilibrium nature, a polariton condensate behaves in an observably different way from its equilibrium counterparts. ²

The behavior follows the form predicted by the Kardar-Parisi-Zhang (KPZ) model, which describes a wide variety of nonequilibrium systems—but until now, only classical ones. The polariton condensate work is the first observation of KPZ physics in a quantum system. It also offers a new way to study phenomena in nonequilibrium statistical mechanics that have stymied theorists and experimenters alike.

Universal fluctuations

When Mehran Kardar, Giorgio Parisi, and Yi-Cheng Zhang developed the KPZ model in 1986, they had in mind a specific type of system: the interface of a stochastically expanding or contracting classical object or region. ³ Although a large number of seemingly disparate interfaces fit the bill—including those of growing crystals, aggregating colloidal clusters, bacterial colonies, statues being eroded by acid rain, and burnt regions of forest or grassland—they’re all fundamentally governed by the same physics. That is, they belong to the so-called KPZ universality class.

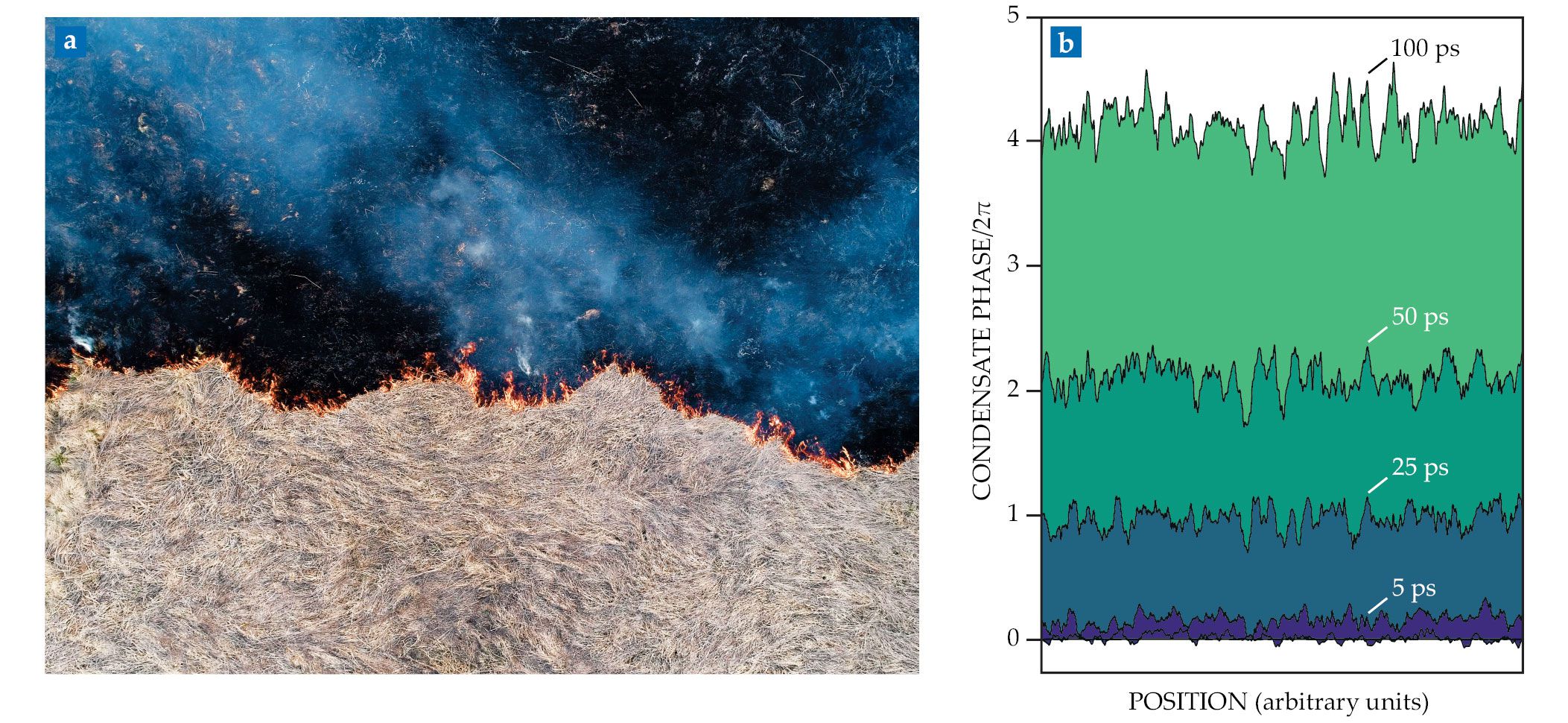
Kardar, Parisi, and Zhang formulated a partial differential equation that describes the interface evolution as a competition between smoothing from diffusion or surface tension, roughening from random noise, and nonlinear growth normal to the surface. From that equation, they started to derive the mathematical properties of the interface shape. In particular, the lumps and bumps of a KPZ interface, such as the wildfire front shown in figure 1a, are characterized by certain power-law correlations that differ from those that arise in systems without the nonlinear growth term. The KPZ model therefore captures the distinctions between a dynamic, growing system and an equilibrium one.

Figure 1.

But discovering all the implications of the KPZ model has taken a decades-long effort that’s still not complete. On the mathematical front, the model’s central equation wasn’t even well defined: It’s a differential equation, but the random noise it introduces is nondifferentiable. The analytical tools for dealing with stochastic noise in linear differential equations existed back in the 1980s, but it wasn’t until 2013 that mathematician Martin Hairer found an approach that would work for the nonlinear KPZ equation. For his work, Hairer was awarded the Fields Medal in 2014.

On the experimental side, it’s extremely challenging to measure an interface’s time evolution—by its very nature, an irreversible and irreproducible process—in enough detail to compute its statistical properties. Although the characteristic power-law correlations were observed in many systems shortly after Kardar, Parisi, and Zhang’s original work, only in 2010 did Kazumasa Takeuchi and Masaki Sano perform a comprehensive analysis of the scaling behavior and fluctuations of a growing interface in a turbulent liquid crystal. ⁴

Today, the KPZ model is well understood in one dimension—that is, for a line-like interface working its way across a planar landscape—but in higher dimensions, little is known. Simulations have offered some insight into the 2D KPZ model. But despite numerous efforts, detailed experiments on 2D interfaces of growing 3D objects are almost entirely absent, and the 2D KPZ equation is unsolved.

Phase transition

Polariton condensates aren’t characterized by interfaces, and they bear little resemblance to other systems in the KPZ universality class. But in 2015 two teams of theorists predicted that the mathematics of the KPZ model should describe the evolving phase of a polariton condensate wavefunction. ⁵ Figure 1b shows a simulation of what it might look like. As time progresses, the average phase advances at a constant linear rate. But the randomness introduced by the photon loss and repumping means that the phase picks up some local fluctuations, just like in any other KPZ interface.

The phase isn’t directly observable, but its correlations can be measured through Michelson interferometry: The light emitted by the condensate is passed through a beamsplitter, one of the beams is sent down a delay line and back, and the beams are recombined. If the time to traverse the delay line is, say, 50 ps, the intensity of the recombined beam measures the correlation of the phase at time t with the phase at time t + 50 ps. The spatial correlations, meanwhile, can be measured directly from the spatially resolved interference pattern. By varying the length of the delay line, one can therefore study the functional form of the phase correlations and test it against the KPZ prediction.

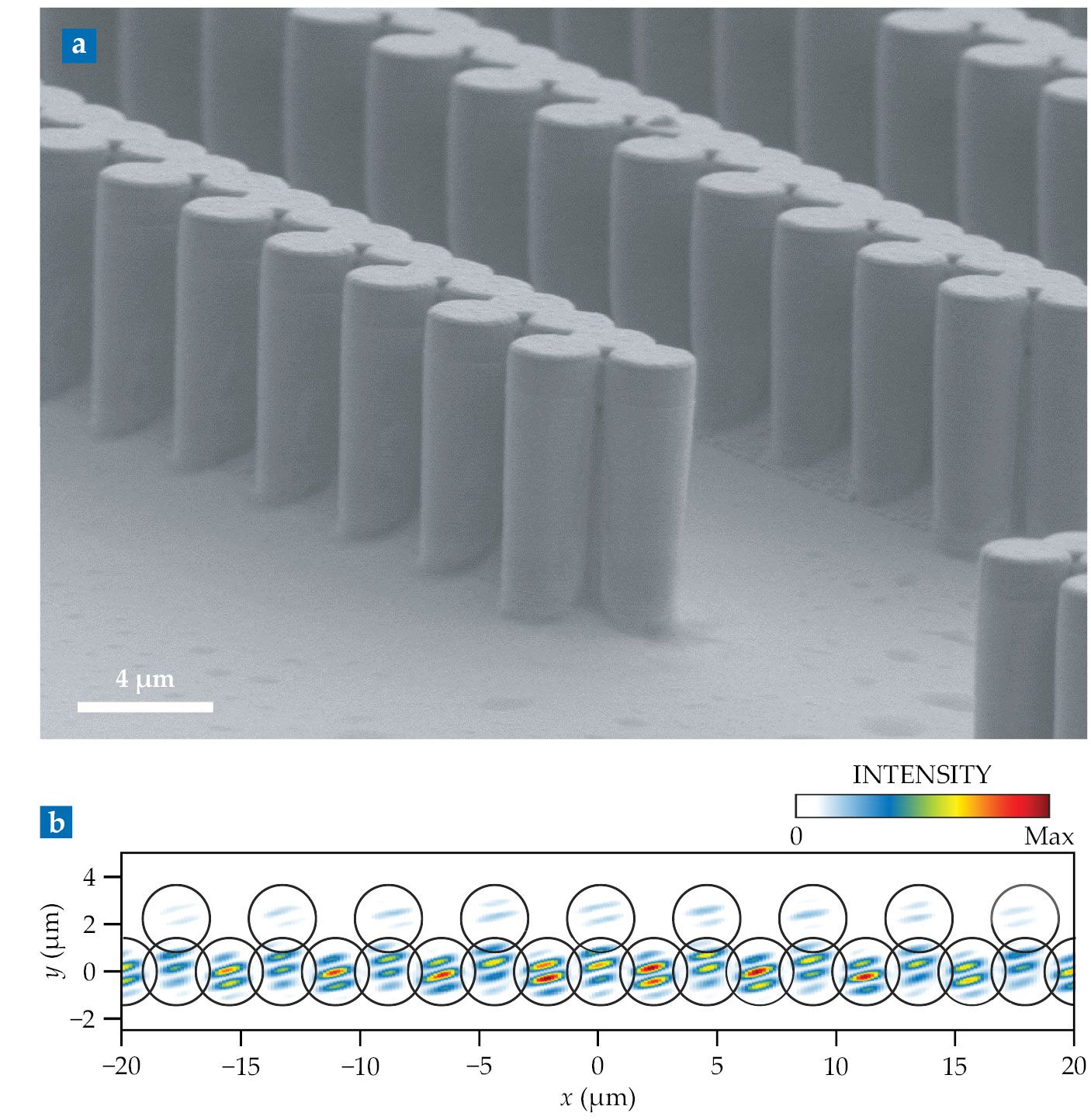
That was the basis of Bloch, Canet, and colleagues’ approach. To best compare with existing KPZ theory, they used a 1D polariton condensate confined to the row of micropillars in figure 2a. The pillars are made of layers of different semiconductor materials, some of which act as mirrors to trap the photons and others of which form the quantum wells that host the solid-state excitations. An example of the measured interference pattern is shown in figure 2b.

Figure 2.

“The biggest challenge was mapping the observations onto the theory,” says Bloch, “to make sure we were measuring the right thing.” Canet elaborates: “Polariton physics is quite far from statistical physics, and we needed to draw on expertise from various communities just to know what the relevant observables were and how to disentangle KPZ physics from other effects.” With Bloch’s experience with polariton experiments, Canet’s expertise in KPZ theory, and collaborator Anna Minguzzi’s knowledge of the theory of Bose–Einstein condensation, the team was able to confirm that the polariton condensate’s phase correlations did indeed adhere to the predictions of the KPZ model.

Confounding vortices

A natural next step is to extend the work from one dimension to two. It’s a lot easier to measure correlations in the phase of a 2D polariton condensate than in, for example, the 2D surface of a 3D expanding forest fire. Polariton condensates might seem to be a gift to the KPZ universality class to launch the model into the next dimension.

But before that can happen, researchers will need to fully understand a complicating factor that distinguishes polariton condensates from other KPZ systems. Whereas the height of a physical interface can be any real number, phase takes values only between 0 and 2π, so a phase of π is the same as a phase of 3π, 5π, 7π, and so on.

A 2D polariton condensate can therefore host phase vortices, where traveling around a closed loop picks up a phase change of some multiple of 2π. The condensate can undergo a phase transition (the Berezinskii-Kosterlitz-Thouless transition; see Physics Today, December 2016, page 14 ) in which vortex–antivortex pairs form and separate. And the vortex dynamics can influence the measured phase correlations, potentially overwhelming the KPZ effects.

Because closed loops don’t exist in one dimension, it might seem that the researchers haven’t yet encountered any vortices. But to their surprise, they found that they have. When they simulated the phase dynamics in 1 + 1 dimensions (that is, one space dimension and one time dimension), vortex–antivortex pairs did show up—and the pairs didn’t necessarily disrupt the KPZ dynamics. When the vortices are sparse enough, the signature KPZ fluctuations still shine through.

The researchers have some ideas for how to lessen the vortex effects in a 2D condensate by shaping the semiconductor lattice that hosts it. But because so little is known about KPZ physics in higher dimensions, it’s hard for them to even speculate about what they might find. “The polariton condensate is really different from an equilibrium Bose–Einstein condensate, and it is far richer than a classical growing interface,” says Canet. “It’s essentially a new state of matter—a new object—and that could lead to some really different applications.”