Physics Nobel Prize to Nambu, Kobayashi, and Maskawa for theories of symmetry breaking

For their contributions to the understanding of symmetry breaking in particle physics, three theorists have been awarded this year’s Nobel Prize in Physics. The Royal Swedish Academy of Sciences awarded half the prize to the University of Chicago’s Yoichiro Nambu “for the discovery of the mechanism of spontaneous broken symmetry in subatomic physics.” The other half is awarded jointly to Makoto Kobayashi of KEK, Japan’s high-energy accelerator research organization in Tsukuba, and Toshihide Maskawa of Kyoto University “for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature.”

All three laureates were born and educated in Japan. But Nambu, born in Tokyo in 1921, is a generation older than Kobayashi and Maskawa, who were born in the early 1940s. And unlike them, Nambu has spent most of his career in the US, having left war-ravaged Japan in 1952 for what he has described as the “paradise” of Princeton, New Jersey.

Spontaneous symmetry breaking

Introduced into particle physics by Nambu in 1960, spontaneous symmetry breaking was to become a pillar of the field’s standard model, which since its completion in the mid-1970s has survived every experimental challenge. When a physical state does not exhibit all the symmetries of the dynamical laws that govern it, the violated symmetries are said to be spontaneously broken.

The idea had been around for a long time in classical mechanics, fluid dynamics, and condensed-matter physics. An oft-cited example is ferromagnetism. Its underlying laws of atomic physics are absolutely invariant under rotation. Nonetheless, below a critical temperature the atomic spins spontaneously line up in some arbitrary direction to create a state that is not rotationally symmetric. Similarly, the cylindrical symmetry of a state in which a pencil is perfectly poised on its tip is spontaneously broken when the pencil inevitably falls over. But such examples give little hint of the subtlety and power of the notion once Nambu began exploiting it in quantum field theory.

It began with a paper Nambu wrote in 1959 about gauge invariance in superconductivity. ¹ The paper exhibits his virtuosity in two disparate specialties—quantum field theory and condensed-matter theory. He became conversant with both as a graduate student at the University of Tokyo after he was mustered out of the army in 1945. Eventually he began working with the group around Sin-itiro Tomonaga, one of the creators of modern quantum electrodynamics (QED). Tomonaga was actually based at another university in Tokyo. But the University of Tokyo was strong in condensed-matter physics. So Nambu started out working on the Ising model of ferromagnetism.

After two years at the Institute for Advanced Study in Princeton, Nambu came to the University of Chicago in 1954, just before the untimely death of Enrico Fermi. When John Bardeen, Leon Cooper, and Robert Schrieffer published their theory of superconductivity in 1957, Nambu and others noted that the BCS superconducting ground state lacked the gauge invariance of the underlying electromagnetic theory. In classical electrodynamics, gauge invariance refers to the freedom one has in choosing the vector and scalar potentials. In QED that freedom is linked to the freedom to change the phase of the electron wavefunction arbitrarily from point to point in space. Did the gauge-symmetry violation mean that the BCS theory was simply wrong? Or perhaps superconductivity was a manifestation of some yet unknown force beyond electromagnetism and atomic physics.

Having heard Schrieffer give a talk about the new theory in 1957 without mentioning gauge invariance, Nambu spent the next two years thinking about its role in the theory. He recast the BCS theory into the perturbative quantum-field-theoretic formalism with which Richard Feynman had solved—independently of Tomonaga—the problem of the intractable infinities in QED. From that reformulation, Nambu concluded that the superconducting ground state results from the spontaneous breaking of the underlying gauge symmetry. He showed that all the characteristic manifestations of superconductivity—including the expulsion of magnetic flux and the energy gap that assures lossless current flow—follow simply from that spontaneous symmetry breaking.

Exploiting an analogy

“I began this work with no thought that it might be relevant to particle physics,” recalls Nambu. But his analysis revealed several possible connections:

The spontaneous symmetry breaking in the BCS theory generated collective excitations of quasiparticle pairs whose frequencies vanished in the limit of long wavelength. In other words, energy vanished at zero momentum—the hallmark of a zero-mass particle. Nambu proposed that such massless, spinless particles or excitations are an inevitable consequence of any theory with spontaneous breaking of a continuous (as distinguished from discrete) symmetry. And indeed a year later theorist Jeffrey Goldstone revisited Nambu’s conjecture and offered a more rigorous and general proof. Then for much of the decade, the supposed inevitability of these so-called Nambu–Goldstone bosons was to pose a frustrating but extraordinarily fruitful problem for theorists seeking quantum field theories of the strong and weak nuclear forces.

Furthermore, Nambu noted that the mechanism by which the spontaneous symmetry breaking generates the BCS energy gap was suggestively analogous to what one would need to generate a nonvanishing nucleon mass in a theory of the strong interactions whose underlying symmetry requires the nucleon to be massless.

Nambu promptly applied those ideas to outstanding problems in particle physics, where, he argued, the analogue of the BCS ground state that manifests the broken symmetry would be the vacuum itself. ²

In Fermi’s 1934 theory of beta decay, the weak interaction of the hadrons (at that time only the proton and neutron) is ascribed to a so-called weak hadronic current analogous to the electron current of electrodynamics. By 1958, a year after the discovery that the weak interactions violate parity conservation, it was clear that one had to add an axial-vector current to the vector current of the Fermi theory. “Vector” and “axial vector” refer to the transformation properties of the currents under mirror inversion (parity).

The vector current was known to be conserved in the sense that like the electromagnetic current, it obeys a continuity equation. It was appealing to suggest that the axial-vector current was also conserved. Conserved quantities imply symmetries. In particular, a conserved axial current implied a chiral symmetry that might serve as the basis for a theory of the strong interactions. Chirality or handedness, refers to whether a nucleon (or any other spin-1/2 fermion) spins like a left- or right-handed screw. A chirally symmetric theory of the strong interactions would be invariant under independent global phase shifts of the left- and right-handed components of the theory’s fundamental fermions.

The problem was that strict chiral symmetry makes all the fermions in the theory massless—which the nucleon certainly is not. If, on the other hand, the nucleon acquires its mass through spontaneous breaking of the chiral symmetry, that breaking should generate a triplet of massless, spinless Nambu–Goldstone hadrons. But they were just as nonexistent as the massless nucleons.

To resolve that bind, Nambu proposed that the chiral symmetry is indeed spontaneously broken. But, he argued, the chiral symmetry of the underlying dynamics is slightly imperfect even before the spontaneous breaking, and therefore the Nambu–Goldstone bosons don’t have to be strictly massless, just much lighter than the nucleon. And for that, the three charge states of the pion (with about 1/7 the nucleon’s mass) fit the bill.

In two follow-up papers with Giovanni Jona-Lasinio, Nambu fleshed out that idea with a simple illustrative theory in which the nucleon, before spontaneous symmetry breaking, has a “bare mass” about 1% that of the physical nucleon. ³ That nonvanishing bare mass mars the underlying chiral symmetry just enough for the spontaneous breaking to generate the pions as bound states of nucleon–antinucleon pairs.

All this was 3 years before the quark model and 12 years before the formulation of quantum chromodynamics, the standard model’s theory of the strong interactions to whose conceptual basis Nambu would soon make seminal contributions. In QCD, nucleons and pions are bound states of quarks about as light as the bare nucleons of Nambu’s illustrative model. And in QCD, it’s the quark masses that mar the theory’s underlying chiral symmetry.

So what’s the lasting value of such an unrealistic model, which made no pretense of being a fundamental theory of the strong interactions? Chiral symmetry was to become the basis of a very useful effective-field theory. “Nambu’s prescient work in the early 1960s profoundly deepened our understanding of mass,” says Princeton University theorist Curtis Callan. “It lets us explain today not only why the pion is so light but also how the proton, a bound state of three almost massless quarks, can be so much heavier than its constituents.”

Electroweak unification

The crowning triumph of spontaneous symmetry breaking was the successful creation of a unified theory of the weak and electromagnetic interactions in 1967 by Steven Weinberg and independently by Abdus Salam. But achieving electroweak unification first required finding the exception to Goldstone’s theorem.

In 1963 condensed-matter theorist Philip Anderson had pointed out that the massless excitations Nambu found in the BCS theory actually acquire mass when one includes Coulomb interactions that the theory explicitly neglects. ⁴ He suggested that the mechanism by which those excitations acquire mass also applies to spontaneous symmetry breaking in a particular class of field theories in particle physics. They are the so-called local gauge theories, which, like QED, remain invariant under independent, arbitrary phase shifts or more complicated transformations of the wavefunction at every point in space and time.

A year after Anderson’s paper, a number of particle theorists worked out in detail how spontaneous symmetry breaking in local gauge theories avoids the embarrassment of spinless, massless Nambu–Goldstone bosons that don’t exist. ⁵ (The chiral symmetry to which the pions were attributed is a global rather than a local symmetry.) In some local gauge theories, for example QED and QCD, the gauge symmetry remains unbroken. Such theories require the existence of massless, spin-1 “gauge bosons” like the photon and the gluons. The theorists concluded that if the gauge symmetry is spontaneously broken, the Nambu–Goldstone bosons mix with the gauge bosons in a way that makes the former disappear and the latter become massive.

Massive gauge bosons had been much sought after. The massless photon mediates the infinite-range electromagnetic force. The very-short-range weak force, by contrast, appeared to require mediators much heavier than the proton. Weinberg proposed that the photon and the massive mediators of the weak interaction are in fact gauge-boson siblings in a unified local gauge theory. ⁶ Their gross disparities of mass and coupling strength, he argued, follow from a spontaneous symmetry breaking that avoids the unwanted Nambu–Goldstone bosons.

The experimental confirmation of the resulting electroweak theory culminated in 1983 with the discovery of the predicted charged (W^±) and neutral (Z⁰) weak gauge bosons—almost a hundred times heavier than the proton. “For me, the most wonderful implication of Nambu’s introduction of spontaneous symmetry breaking in the early 1960s was that there were heavily disguised symmetries in nature that remained to be discovered,” recalls Weinberg.

Kobayashi and Maskawa

When it was discovered in 1957 that the weak interactions are not invariant under mirror inversion (denoted by the parity operator P), theorists generally assumed that the laws of particle physics nonetheless remain invariant under CP , the combined transformations of parity and charge conjugation (C). In other words, particle interactions should be indistinguishable from those of their antiparticles as viewed in a mirror. But that strategic retreat became untenable in 1964, when it was found that about one time in a thousand, a neutral K meson decays in a way that violates CP invariance.

Parity violation had been explained by positing that only the left-handed spin components of the fundamental spin-1/2 fermions (and the right-handed components of their antiparticles) participate in the weak interactions. But such schemes appeared to be CP -invariant, thus leaving the violation unexplained. Theorist Lincoln Wolfenstein promptly suggested that the observed CP violation might involve a “superweak” interaction outside the purview of the ordinary weak interactions that was, indeed, unique to the neutral-kaon system.

Not until 2001 was CP violation finally observed in another system: the decay of neutral B mesons. The B mesons, 10 times heavier than the kaons, carry the very heavy bottom quark, which was discovered in 1977. But its existence had been predicted by Kobayashi and Maskawa in their 1972 quest to explain CP violation as a consequence of the ordinary weak interactions. ⁷

Maskawa and Kobayashi were both born in Nagoya (in 1940 and 1944) and did their PhDs in the particle-theory group led by Shoichi Sakata at Nagoya University. In the 1950s Sakata had formulated an influential precursor to the quark model. “Maskawa and I first met when he was a teaching assistant in one of my undergraduate courses,” recalls Kobayashi. After Kobayashi finished his PhD, the two were reunited as post-docs at Kyoto University in 1972 and together undertook the investigation that would win them the Nobel Prize.

By 1972, even though the predicted W and Z bosons were still to be discovered, the Weinberg–Salam model was already the presumptive theory of the weak interactions. But to make predictions about decays involving hadrons, one has to augment the model with information about the quark content of the weak hadronic currents. At the time, only three flavors of quarks were known: up (u^+2/3), down (d^−1/3), and strange (s^−1/3). But Sheldon Glashow, John Iliopoulos, and Luciano Maiani had already made a strong theoretical case (the so-called GIM model ⁸ ) for the existence of a fourth quark, which they called charmed (c^+2/3). The charmed quark would be discovered in 1974.

In a quantum field theory, the CP operator transforms fields into their complex conjugates. Unless one embellishes the basic Weinberg–Salam model with additional scalar fields, the only way it could yield CP violation is if one or more of the coupling constants that couple the W boson to the different quark flavors is irreducibly complex—in the sense that its phase cannot be made to vanish by clever redefinitions or phase conventions.

Before Kobayashi and Maskawa set to work seeking the origin of CP violation within the confines of the basic Weinberg–Salam model, it was already clear that a theory with only the three known quarks could yield no such complex coupling constant. Therefore they looked first at the GIM scheme, in which the four quarks come in two pairs—(u,d) and (c,s)—closely related, respectively, to the lepton pairs (e⁻, v _e) and (µ ⁻, v _µ ). Each quartet of two quarks and two leptons is nowadays called a family of the fundamental fermions.

Mixing flavors

In the GIM scheme, the quark flavor eigenstates u, d, s, and c are not quite the weak-interaction quark eigenstates in the hadron currents that couple to the W. The two sets of basis states are related by a rotation through a small mixing angle θ in two dimensions of the flavor space. Called the Cabibbo angle, θ was introduced by Nicola Cabibbo in pre-quark days (1963) to preserve the universality of the weak interactions in spite of nature’s observed preference for decays that do not change strangeness.

Kobayasahi and Maskawa pointed out that, in this four-quark scenario, the relevant coupling constants among which one must seek an irreducible phase are just the matrix elements of the 2 × 2 Cabibbo rotation matrix (times a universal constant g). For example, the coupling constant for the udW vertex in the Feynman diagram on page 18 would be g cosθ, while the weaker coupling constant for the strangeness-changing vertex usW would be g sinθ. All the coupling constants would be real. They would be determined by the one parameter θ, with no extra degree of freedom for an irreducible phase. Therefore the basic Weinberg–Salam model with only the four GIM quarks offered no mechanism for CP violation.

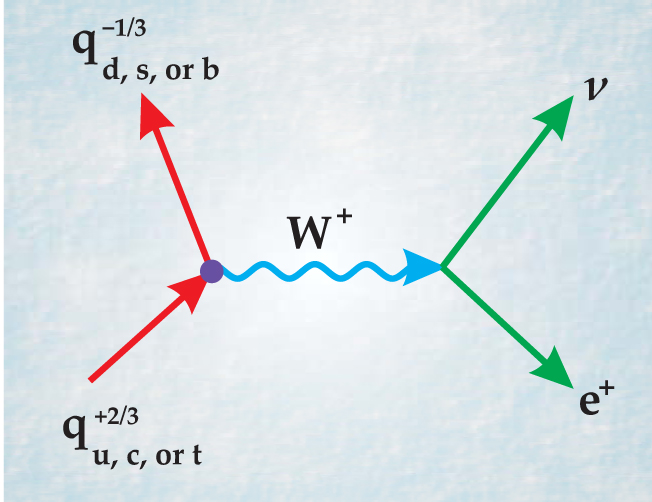
Then Kobayashi and Maskawa went on to systematically eliminate all the other, “less natural” four-quark scenarios that were consistent with the Weinberg–Salam model. Those that did allow an irreducible phase turned out to be incompatible with well-established empirical characteristics of hadronic decays. Thus the authors had shown that no realistic four-quark scheme would do. So they went on to consider an expansion of the GIM scheme by adding a putative new pair of quarks to make six.

Called by their present names, the new quarks would be the bottom (b^−1/3) and the top (t^+2/3). The Cabibbo matrix then generalizes to become a 3 × 3 mixing matrix describing a rotation in three dimensions of flavor space. The expanded Cabibbo-Kobayashi-Maskawa (CKM) matrix has four degrees of freedom: three rotation angles and, most important, an irreducible phase that might be responsible for the observed CP violation.

In effect, Kobayashi and Maskawa were predicting that unless the CP violation was due to new physics beyond the basic Weinberg–Salam model, there had to be a third family of quark and lepton pairs. “Our paper began to attract real attention when the [heavy] τ lepton was found in 1975,” says Kobayashi. And then, after the discovery of the bottom quark two years later, the paper became one of the most cited in the history of particle theory. The top quark, almost 200 times heavier than the proton, was not discovered until 1994.

B factories

The nine elements of the unitary CKM matrix are the relative coupling constants for the nine different q^+2/3q^−1/3W⁺ vertices indicated in the figure. If the irreducible phase is not zero, no phase convention can make them all real. One can measure all the CKM matrix elements in a variety of processes that do not exhibit CP violation, and from them predict where and how strongly CP violation will occur—assuming that a nonzero CKM phase is indeed the cause.

Because the B mesons are so heavy, they were expected to offer experimenters a rich variety of decay modes that would exhibit CP violation much better than the kaon decays for comparison with the CKM predictions. To that end, the “B factories” KEKB at KEK and PEPII at SLAC were built in the late 1990s. Both facilities first confirmed CP violation in B decays in 2001 (see May 2001, page 17 ). And since then, all their results have been consistent with what the CKM matrix predicts.

That’s gratifying for particle theory but problematic for cosmology. The overwhelming preponderance of matter over antimatter in a cosmos that presumably began with neither requires some source of CP violation. (See the article by Helen Quinn in February 2003, page 30 .) But cosmologists conclude that the CP violation offered by the Kobayashi–Maskawa mechanism, though it explains what’s been seen in meson decays, is far too weak to explain the cosmic asymmetry. There must be additional CP -violating phenomena in nature.

Kobayashi, who retired from the directorship of KEK’s Institute of Particle and Nuclear Studies in 2005, is still investigating the symmetry-violating implications of various theories that propose new physics beyond the standard model. Maskawa, having retired from the faculty of Kyoto University’s Yukawa Institute for Theoretical Physics in 2003, is now a professor at Kyoto Sangyo University.