Physics Nobel Prize Goes to Gross, Politzer, and Wilczek for Their Discovery of Asymptotic Freedom

Particle theorists David Gross, David Politzer, and Frank Wilczek have been awarded this year’s Nobel Prize in Physics “for the discovery of asymptotic freedom in the theory of the strong interactions.” The laureates are, respectively, professors of physics at the University of California in Santa Barbara, Caltech, and MIT. The discovery was made in 1973 by Gross and Wilczek ¹ at Princeton University and, independently, by Politzer ² at Harvard University. At the time, Wilczek was Gross’s graduate student and Politzer was a graduate student of Sidney Coleman.

Asymptotic freedom refers to the vanishing of the strong nuclear force between quarks as the distance between them goes to zero. The surprising discovery by Gross, Wilczek, and Politzer that a certain class of quantum field theories has this property led quite quickly to quantum chromodynamics (QCD), the now standard theory of the strong interactions (see the article by Wilczek in Physics Today, August 2000, page 22 ). The dauntingly complex laboratory manifestations of the strong interactions had prompted Freeman Dyson in the late 1950s to predict pessimistically that it might be 100 years before a proper theory emerged.

Why call the freedom of quarks at small separations “asymptotic,” which to the uninitiated suggests large distances? The arcane nomenclature invokes the reciprocal relation between length and momentum in quantum mechanics. The reference is to asymptotically high momenta. Probing the short-distance interaction of quarks inside a nucleon requires scattering experiments in which a high-energy probe particle transfers a large fraction of its momentum to a target nucleon.

Deep-inelastic scaling

Quite unexpected results from a series of such experiments at SLAC had been puzzling particle theorists since 1969. Ateam led by Jerome Friedman, Henry Kendall, and Richard Taylor was measuring the deep-inelastic scattering of high-energy electrons off protons—that is, inelastic scattering events in which the electron suffers a large momentum transfer q. It turned out that the dependence of the differential scattering cross section on q and ν, the electron’s energy loss in the collision, was peculiarly constrained: The cross section seemed to depend only on the ratio q ²/ν.

Theorist James Bjorken soon explained this “scaling” behavior of the SLAC deep-inelastic scattering data in terms of Richard Feynman’s 1969 conjecture that the nucleon is made up of individual pointlike “partons.” It was not yet clear that these partons were, in fact, the fractionally charged quarks hypothesized by Murray Gell-Mann and George Zweig in 1964. The deep-inelastic scaling, Bjorken pointed out, would be just what you’d expect if the electrons were scattering off partons that rattle around perfectly free inside the nucleon, unaffected by any nuclear force other than the long-distance constraint that keeps them confined.

This picture of partons free at short distances was appealingly simple. But it seemed to make no sense in the search for a real theory of the strong interactions. How could hadrons—the particles that experience the strongest force in nature—be made of constituents that are oblivious of each other at short distances? In quantum electrodynamics (QED), the paradigm of quantum field theories, the electric force between point charges increases with proximity. With growing distance, the effective charge of the electron is decreased by vacuum screening. The relativistic quantum vacuum, constantly sprouting polarizable pairs of virtual electrons and positrons, screens charge very much like a dielectric. That’s just the opposite of what one would need for a quantum field theory of the strong interactions that could explain deep-inelastic scaling.

Down with field theory!

“Field theory was in bad repute in the 1960s,” recalls Gross, “especially in Berkeley,” where he finished his PhD under Geoffrey Chew in 1966. Chew and his disciples argued that a few very general principles such as analyticity, unitarity, and various symmetries would suffice to yield a unique universal scattering matrix for the strong interactions. Field theories, they contended, introduce unobservable, fictitious entities. In any case, the “nuclear democracy” of the so-called S-matrix approach recognized no fundamental constituents on which a field theory could be built. Every hadron species was as fundamental or as composite as any other; and no one had ever seen a quark. But even if one could create a legitimate field theory of the strong interactions, the argument went, it would be largely useless for calculating anything because perturbation expansions in powers of the coupling constant wouldn’t con verge. Unlike the small coupling constants of the electromagnetic and weak interactions, the strong coupling constant was so big that perturbative calculations would yield nonsense.

As a postdoctoral Harvard junior fellow (1966–69), Gross began a productive collaboration with Curtis Callan that continued when both moved on to Princeton in 1969. Much of their work involved the formulation of experimentally testable sum rules based on the algebra of hadronic-current operators in quantum field theories. Current algebra was, at the time, a kind of halfway house between the S-matrix approach and field theory. Gell-Mann had pointed out that one could learn about the fundamental makeup of hadrons by abstracting rules for hadronic currents involved in electromagnetic and weak interactions from model field theories one didn’t have to believe in. He likened it to the haute cuisine practice of cooking a pheasant breast between slices of veal and then discarding the veal.

By 1972, the application of current-algebra sum rules to deep-inelastic electron and neutrino scattering data had convinced Gross that quarks were real dynamical constituents of nucleons. Applying the Callan–Gross sum rule to the data clearly showed that the only components of the nucleon that coupled to bombarding electrons or neutrinos were pointlike spin-^1/2 objects—just what one expected of quarks. Applying other sum rules to the data showed that these constituents also had the fractional charge and baryon number expected of quarks.

“At the end of 1972, I undertook to settle the issue of the validity of quantum field theory by proving that no field theory could explain deep-inelastic scaling,” recalls Gross. “I would show that there are no nontrivial asymptotically free field theories.” Within a few months, Gross and Coleman had largely completed the proof for most renormalizable field theories. But they had not yet tackled a particularly difficult and subtle class: the non-abelian gauge theories.

QED is an abelian, locally gauge-invariant field theory. That is, the theory is invariant under phase shifts of the electron’s wave function that differ arbitrarily from point to point. Invariance is preserved by applying a compensating gauge transformation to the electromagnetic vector potential at every point. In fact, the unbroken local gauge invariance, by itself, fixes the nature of the interaction and dictates that it be mediated by spin-1 massless photons. In group-theoretic terminology, the theory is called abelian because simple phase shifts commute with one another.

The Yang–Mills loophole

In 1954, searching for a field theory of the strong interactions, Chen-Ning Yang and Robert Mills generalized the notion of local gauge invariance from simple phase shifts to rotations in isospin space. Just like rotations in ordinary space, rotations in the abstract isospin space do not commute. Hence the appellation non-abelian. Yang and Mills failed to find a satisfactory theory of the strong interactions, but the Yang—Mills idea of non-abelian gauge theory did bear fruit in the late 1960s, in a unified field theory of the electromagnetic and weak interactions. And in 1971, Gerard’t Hooft made the particle-physics community take the electroweak unification theory seriously by showing that such Yang–Mills theories are renormalizable—that is, one can subtract away the nonphysical infinities that they, like all quantum field theories, inevitably generate.

With Wilczek, who had come to Princeton in 1970 after earning his undergraduate degree in mathematics at the University of Chicago, Gross set out to complete the demolition of strong-interaction field theories. “Frank was my first graduate student,” says Gross. “He spoiled me. I thought they’d all be that good.” Wilczek himself was particularly interested in studying the high-energy behavior of the electroweak theory.

In QED, as in almost all renormalizable field theories, the effective coupling constant decreases as the fermions get farther apart. It only remained to show that the same was also true for all Yang–Mills theories. The formidable task of examining how the coupling varies with distance was made easier by a renormalization-group formalism developed by Callan and, independently, by Kurt Symanzik on the basis of a 1954 paper by Gell-Mann and Francis Low and later work by Kenneth Wilson. In renormalizable field theories, the coupling constant must be dimensionless. But renormalization requires the introduction of an arbitrary mass scale. Of course, the observable consequences of the theory cannot depend on that arbitrary renormalization scale. “This physical triviality is given mathematical expression by the Callan–Symanzik equations,” explains Coleman. “But they yield highly nontrivial information about the asymptotic behavior of the theory.”

The formalism introduces a differential equation that governs a function β(g), where g, the effective coupling constant, is itself a function of distance—or, equivalently, of momentum transfer. The Callan–Symanzik β function is essentially the negative of the logarithmic derivative of g with respect to distance. The sign convention is important. The field theory possesses asymptotic freedom if and only if the sign of the β function becomes negative as g goes to zero.

The telltale sign of β

Callan and Symanzik had provided an acid test for asymptotic freedom. And the telltale limiting sign of β could be reliably calculated from Feynman diagrams corresponding to the lowest-order perturbative expansion in g. Nonetheless, the actual calculation for Yang–Mills theories was laborious and fraught with pitfalls. “Nowadays it’s a straightforward, though still laborious homework problem in field theory courses,” says Wilczek. “But the theoretical tools available back then were primitive, and it’s always easier to do a calculation when you already know the answer.” Sign mistakes were a particular hazard. “One last sign mistake convinced us for a few days that the β function limit was positive—that we had proven what David set out to prove.”

But after more checking, it became clear that there were indeed asymptotically free Yang–Mills theories. For the most plausible of these, given what was known about the strong interactions, the non-abelian local gauge symmetry was invariance under rotation of the quark wavefunctions in the abstract space of three “colors” described by the Lie group SU (3). In that particular case, which soon turned out to be the heart of QCD, Gross and Wilczek found that the coefficient of the lowest-order term in the perturbation expansion of the β function in g was proportional to $-\left(11/2-n/3\right)$ , where n is the number of distinct quark flavors.

This result implies that the theory is asymptotically free so long as there are no more than 16 flavors of quarks with masses less than qc, where q is the momentum-transfer scale at which a hadron is being probed. Three flavors (up, down, and strange) were known in 1973, and there is good reason to believe that there are no more than the six quark flavors we know now. Too many different varieties of light quarks would be a problem because vacuum creation of virtual quark–antiquark pairs tends to subvert asymptotic freedom by screening the color charge in much the same way that virtual e⁺e⁻ pairs screen charge in QED.

Under color- SU (3) symmetry, each quark flavor comes in three absolutely equivalent colors. The notion of hadronic color was introduced by O. W. Greenberg and, independently, by Yoichiro Nambu and Moo-Young Han in the mid-1960s to add a new degree of freedom that would resolve a quantum-statistics paradox in the early quark model. Nambu soon suggested a color- SU (3) gauge field as the source of the strong interactions. Color, he was saying, might be the generalized analog of electric charge for the strong force. And that, indeed, is its role in QCD.

Politzer’s calculation of the negative limiting sign of the β function was essentially identical and simultaneous with that of Gross and Wilczek. But Politzer had come to the task with a different purpose in mind. In 1972, Coleman and Erick Weinberg, another of his Harvard students, had discovered a possible mechanism for dynamical symmetry breaking in QED, and they had begun to generalize it to non-abelian theories. Politzer thought that calculating the β function for the non-abelian case might give additional insight into the symmetry breaking, and that it might be a suitable thesis topic.

He assumed, at first, that the β function would yield the information he sought about the low-momentum (long-distance) behavior of the Yang–Mills theories, as it does for abelian theories. But he soon found, as Gross and Wilczek did, that β was negative at small g. It was useless for examining electroweak interactions at large distances, but it meant asymptotic freedom, which was just what was needed for a theory of the strong interactions.

In high excitement, Politzer phoned Coleman, who was spending the spring of 1973 on sabbatical at Princeton, to report his “stupendous” discovery. But Coleman put a temporary damper on Politzer’s enthusiasm. Gross, still under the influence of a momentary sign blunder, had just assured him that Yang–Mills theories cannot be asymptotically free. But Wilczek soon found the offending sign error and Politzer, having rechecked his own calculation, was confident in the negative leading term of the β function. The two discovery papers appeared back-to-back in the 25 June 1973 issue of Physical Review Letters.

The following summer, Politzer, as a junior fellow at Harvard working with Thomas Appelquist, applied the concept of asymptotic freedom to the heavy “charmed” quark, which had not yet been seen. But its existence was confidently predicted by Sheldon Glashow and coworkers. Appelquist and Politzer calculated that, if the charmed quark exists, it should form a bound charm–anticharm state with an extraordinarily narrow width plus a positronium-like set of excited “charmonium” states. The system would resemble positronium, they argued, because asymptotic freedom renders the strong force between the heavy quarks coulomb-like at distances appropriate to heavy-quark bound states.

By the time arguments with the editors of Physical Review Letters about the neologism “charmonium” had been settled, the historic discovery of the J/ψ—the first charmonium state—had been announced on 11 November 1974. The Appelquist–Politzer paper, ³ appearing two months later, took due note of the discovery. “The discovery of charmonium was a huge psychological boost for asymptotic freedom,” recalls Wilczek.

Understanding and testing QCD

“Our first paper ¹ already had the full-blown QCD Lagrangian,” says Gross. But some things were still unclear. On its face, the color- SU (3) gauge theory implies that the strong force between quarks is mediated by massless spin-1 “gluons”—multicolored analogs of the photon. But why hadn’t such particles been seen? Most likely, it seemed, the gluons were rendered very massive by spontaneous symmetry breaking, as are the heavy vector bosons of the electroweak theory. Now we know that color symmetry is unbroken and that the gluons are indeed massless but inescapably confined inside hadrons, as are the quarks. Confinement in QCD has taken longer to understand than asymptotic freedom. “I hold the minority opinion that confinement is still largely a mystery,” says Ken Wilson.

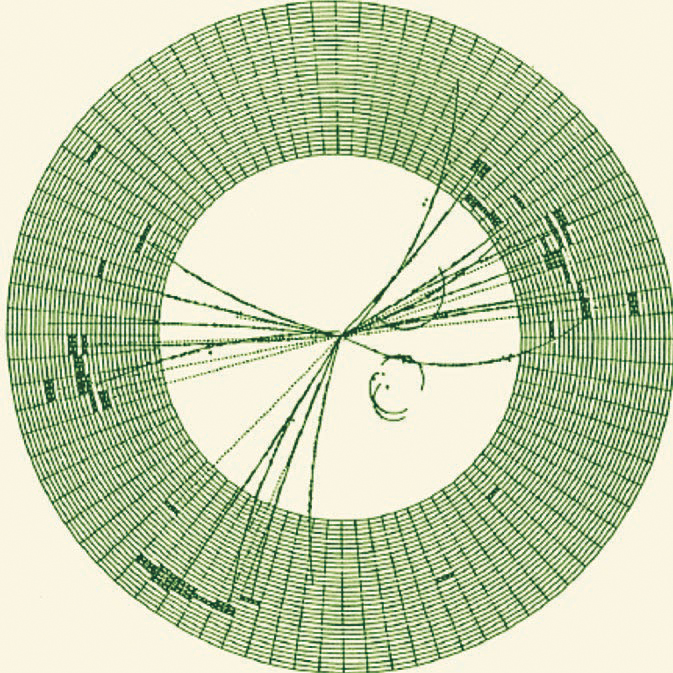
Despite their absolute confinement, the reality of quarks and gluons is nowadays made vividly manifest by the highly collimated jets of hadrons they occasionally generate in e⁺e⁻ collisions at sufficiently high energies. QCD predicts very accurately the energy-dependent cross section for producing events like that in figure 1, whose three jets reveal two quarks and a gluon.

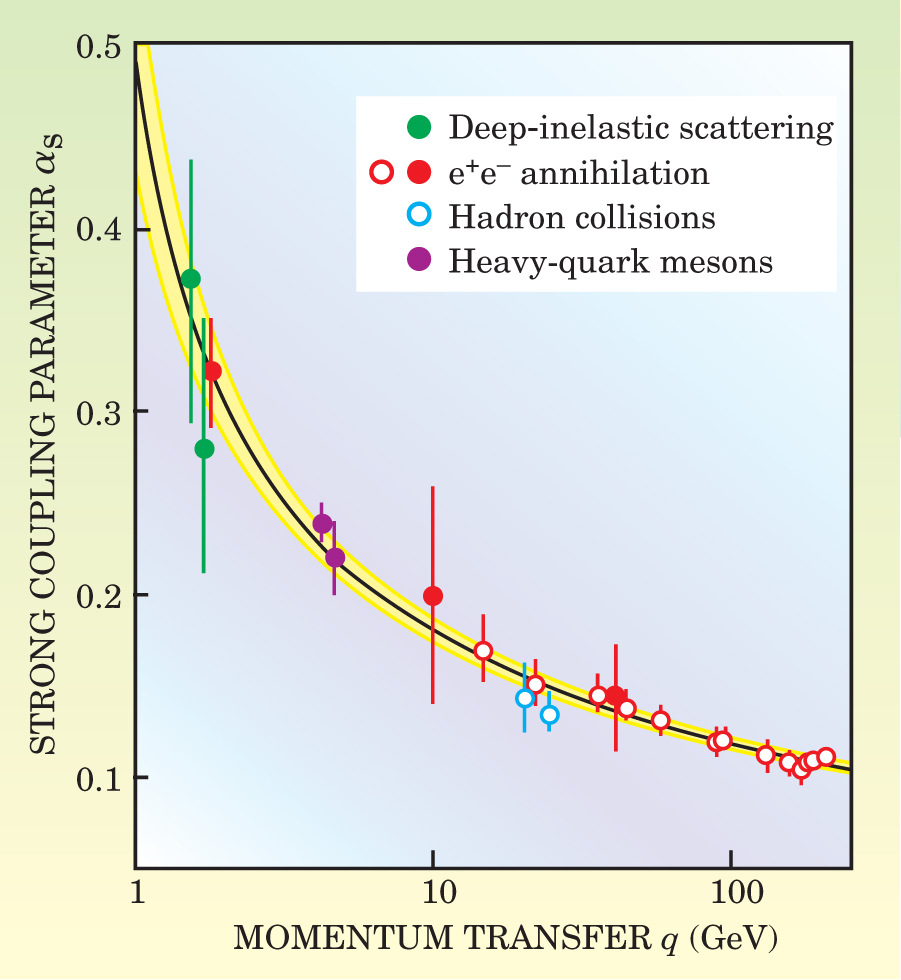
Further strong evidence for the validity of QCD comes from small logarithmic departures from deep-inelastic scaling at energies much higher than those of the original SLAC experiments. Gross and Wilczek pointed out, in a longer followup paper, ⁴ that QCD requires such corrections to naive Bjorken scaling. And their prediction was amply confirmed by experiments at CERN in the late 1970s. Figure 2 shows how well QCD predicts the hallmark of asymptotic freedom, namely, the momentum dependence of the strong coupling constant.

Asymptotic freedom has ramifications far beyond QCD. “The weakening of the strong force at high energies, together with the mathematical resemblance between QCD and the electroweak theory,” says Wilczek, “makes possible the quantitative examination of ambitious schemes for a grand unification of the two.” Just before asymptotic freedom was discovered, Steven Weinberg had written that in the first microseconds after the Big Bang, at temperatures above 10¹² K, “we encounter theoretical problems of a difficulty beyond the range of modern statistical mechanics.” ⁵ Wilczek says that “the discovery of asymptotic freedom dispelled this pessimism overnight. At those primordial temperatures and densities, matter actually becomes weakly interacting and you can calculate its equation of state.”

The laureates

Politzer was born in New York City in 1949. The story is told that, after this year’s Nobel prizes were announced, he received a congratulatory call from an old high-school classmate. “I always knew,” said the classmate, “that you’d be the first in our class to win the Nobel prize.” “Not quite!” Politzer had to reply. He’d been beaten to Stockholm by Russell Hulse, another member of the Bronx High School of Science class of 1966, who shared the 1993 physics prize with Joseph Taylor for their discovery of binary pulsars. Politzer earned his undergraduate physics degree at the University of Michigan. He’s been on the Caltech faculty since 1975.

Wilczek is also a native New Yorker, born in 1951. “The commute to Bronx Science was too far,” he recalls, “but I got a terrific education at Martin Van Buren, my local high school in Queens.” He started at Princeton in 1970 as a graduate student in math. “But taking Gross’s field theory course showed me my true vocation.”

Wilczek taught at Princeton until 1981, when he moved to UC Santa Barbara, where he was appointed the first permanent member of the Institute of Theoretical Physics. From 1990 to 2000, he was at the Institute for Advanced Study in Princeton. Since then he has been at MIT.

The Santa Barbara institute is now called the Kavli Institute for Theoretical Physics, and Gross is its director, having left Princeton in 1997 to take that post. He was born in Washington, DC, in 1941. When he was 12, the family moved to Israel, where his father served as an economic adviser with a US delegation. Gross’s undergraduate education in physics was at the Hebrew University of Jerusalem.

A historical footnote: In the summer of 1972, ‘t Hooft already knew that the small-g limit of the β function can be negative for Yang–Mills theories. That he had done the calculation is clear from a public comment he made after a talk by Symanzik. But ‘t Hooft’s comment was not widely known, and he didn’t publish his result until several months after the discovery papers had appeared. ⁶ In any case, for his earlier proof that Yang–Mills theories are renormalizable, ‘t Hooft shared the 1999 physics Nobel prize with Martinus Veltman.