Matter-wave metrology meets cavity optics

You don’t weigh the same in Boston as you do in Berlin. Granted, the difference—a consequence of Earth’s rotation and unevenly distributed mass—is minuscule, but it’s easily detected with state-of-the-art gravimeters. In fact, atom interferometers can detect Earth’s gravitational pull to better than one part in 10¹¹, which makes them sensitive enough to register the change in gravity due to a change in elevation of just a few millimeters. ¹

The interferometers exploit the wave nature of matter: Pulses of light are used to deliver momentum kicks that split a free-falling atom into two wavepackets, steer them along separate paths through space, and recombine them. The constructive or destructive nature of the wavepackets’ interference reveals information about the respective distances they traveled and the acceleration they experienced.

The resulting ultraprecise measurements are more than curiosities. They can be used to locate buried mineral deposits and to monitor aquifers, and they could conceivably provide a basis for global positioning systems that work underground. (For more on matter-wave interferometry, see the article by Markus Arndt, Physics Today, May 2014, page 30 .)

Atom interferometry was still relatively new when Holger Müller joined the field as a postdoc more than a decade ago. Müller, now at the University of California, Berkeley, recalls an offhand suggestion that his PhD adviser, Achim Peters, made around that time: “Someday, somebody should put an atom interferometer inside an optical cavity.”

The idea had been floating around for a while. Because optical cavities amplify certain resonant modes of light, they can, in theory, be used to deliver bigger momentum kicks using lower- energy pulses. Because they suppress nonresonant modes, they can also narrow a pulse’s linewidth and refine its wavefront, which would make each kick more precise.

Realizing the proposal, however, was fraught with technical stumbling blocks. Now, some 10 years later, Müller and coworkers at UC Berkeley have succeeded in operating a cesium atom interferometer inside a half-meter optical cavity. ² In a proof-of-principle experiment, they demonstrated that the interferometer, pictured in figure 1, can achieve precision comparable to that of conventional atom interferometers while using far less power—microwatts instead of milliwatts. The work could lead to new classes of compact, portable gravimeters and accelerometers.

Cavity gravimetry

As in conventional atom interferometry, the Berkeley group manipulates atoms using two-photon Raman transitions. If two incident photons have a frequency difference that corresponds to a hyperfine transition, they can transfer their momenta to the atom via a sequence such as the one illustrated in figure 2a: The atom recoils from the absorption of the first photon, recoils again from the emission stimulated by the second, and in the process is pumped into a new angular momentum state F. If the two incident photons are counterpropagating, both recoils are in the same direction and the atom receives a momentum kick equal to twice the average photon momentum ℏk.

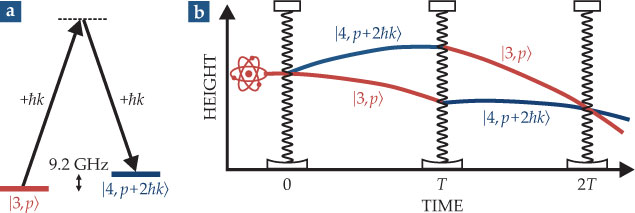
To build an interferometer based on those transitions, one needs to orchestrate a succession of pulses known as a Mach–Zehnder sequence. Figure 2b shows a Mach–Zehnder sequence based on a transition between the F = 3 and F = 4 angular momentum states in the Cs ground level. A first pulse places the freefalling Cs atom in a coherent superposition of two states—one that received a momentum kick and another that didn’t. The two components form distinct localized wavepackets travelling along distinct trajectories. A second pulse inverts the wavepackets’ states, and a third mixes them and causes them to interfere.

The pulse sequence, analogous to the Ramsey sequence (see the article by Serge Haroche, Michel Brune, and Jean-Michel Raimond, Physics Today, January 2013, page 27 ), has become commonplace in quantum optics. But pulling it off inside an optical cavity is tricky. The two laser frequencies must simultaneously meet two strict criteria: Their frequency difference must be tuned precisely to the atomic transition, and their absolute frequencies must each be tuned to a cavity mode. In essence, Müller and his colleagues had to custom tailor their cavity to ensure that the cavity length was an integer multiple of half wavelengths for both frequencies used in the transition.

An optical cavity also seemingly presents a degeneracy problem. In an atom interferometer, a particular Raman transition needs to produce a kick in a particular direction. That’s straightforward to accomplish in free space: If one wants to ensure, for instance, that promotion from the F = 3 to the F = 4 state generates an upward kick, one simply directs the higher-frequency pulse upward and the lower-frequency one downward. In an optical cavity, however, both modes necessarily propagate in both directions as they reflect between the cavity mirrors. To first approximation, any two-photon transition is just as likely to yield a downward kick as an upward one.

As it turns out, however, the Doppler shift experienced by a free-falling atom can lift the degeneracy. By detuning the pulses’ difference frequency by an amount equal to the Doppler shift, the researchers can choose to kick the atom either upward or downward. The cavity itself is just forgiving enough to permit that; the linewidths of the cavity modes are large enough that the researchers can detune the pulses from the atomic transition and still keep them resonant with the cavity.

To make a gravity measurement, the researchers release a cloud of 10⁸ cold Cs atoms into a vacuum chamber inside the optical cavity and then implement the pulse sequence illustrated in figure 2. Because the atoms accelerate under gravity during the course of each measurement, the detuning required to offset the Doppler shift changes, at a constant rate, between the first and last pulses. Through trial and error, the researchers identify the sweep rate that best compensates for the atom’s acceleration—that is, the sweep rate for which the atoms’ final state is independent of the time T between pulses. From that rate they can use a simple formula to back out the acceleration due to gravity.

Size matters

In their proof-of-principle experiment, Müller and his coworkers showed that they could match the sensitivity of similar-sized conventional atom interferometers using orders-of-magnitude less power—just 50 µW. That could pave the way to energy-efficient interferometers that can ride aboard satellites and space probes, where they could be used, for instance, to test predictions of general relativity.

In addition to using the cavity to save power, the researchers could also use it to gain precision. An interferometer becomes more precise as the separation between its arms—in this case, the wavepacket trajectories—grows. In an atom interferometer, that means increasing either the time the atom spends in freefall or the magnitude of the momentum kicks it receives. The former calls for increasing the instrument’s length; so far, the record is a 10-m-tall interferometer, built at Stanford, that permits more than two seconds of free fall. ¹

The Berkeley team seeks to enhance precision by implementing bigger momentum kicks. The intracavity amplification of a moderately strong laser pulse should yield fields intense enough to instigate many-photon atomic transitions. Instead of exploiting two-photon transitions, says Paul Hamilton, the paper’s lead author, “we’d like to push it to 50 or 100 photons.”

To do that, however, they’ll first need to devise a method to cool their atom clouds substantially below the roughly 2 µK achieved in their proof-of-principle demonstration. “When you’re applying really big momentum kicks,” explains Hamilton, “the atoms’ initial velocity needs to be very well defined.”

“It’s a technical hurdle,” Müller adds. “But it’s the type of hurdle we’ve overcome many times in the past.”