Lab experiments mimic the origin and growth of astrophysical magnetic fields

Magnetic fields permeate the space between objects throughout the universe, from galaxy clusters to protogalaxies to nebulae like the one shown in figure 1. It’s not difficult to explain how those fields might be initiated: Weak fields originate in astrophysical plasmas through various mechanisms—for example, temperature or density gradients in the plasma that alter electron trajectories.

Figure 1.

But it remains challenging to demonstrate how seed fields of 10⁻²¹ gauss in intergalactic space grow to their measured astronomical values of several microgauss. Theory suggests that turbulent motion in an astrophysical plasma amplifies tiny magnetic fields by converting kinetic energy into magnetic energy. Such a self-sustaining energy conversion mechanism is called a dynamo.

Dynamos are often distinguished between large scale and small scale. The familiar large-scale geodynamo relies on Earth’s symmetry-breaking rotation to generate a magnetic field that grows at scales larger than those of the liquid-core motion. But in a small-scale dynamo, the magnetic field grows below the length scales of fluid motion. There, turbulence operates first at the smallest length scales, where it rapidly amplifies the fields. The mechanism works even in isotropic conditions.

Now Gianluca Gregori (Oxford University), Petros Tzeferacos (University of Chicago), and colleagues have measured the amplification of a magnetic field in a turbulent laboratory plasma and provided the first physical demonstration of a dynamo resulting from turbulent motion. ¹ The study shows that the turbulent dynamo could be a viable mechanism for magnetic field amplification in the lab and in astrophysical settings.

Galaxies far, far away

To sustain a dynamo, a fluid needs to be electrically conductive, and its motion cannot be too symmetric. Dynamo conditions also require that the magnetic field lines stay in the plasma, rather than diffusing away. Those conditions are easily satisfied by the turbulent, high-temperature, high-velocity plasma that fills intergalactic space.

Even though conditions favorable for dynamos are common in astrophysical settings, the strong turbulence is extremely difficult to replicate in the lab. (See the article by Daniel Lathrop and Cary Forest, Physics Today, July 2011, page 40 .) Astronomical x-ray observations provide information about the temperature, density, and composition of hot plasmas in the universe. But observations cannot convey the geometry and topology of the magnetic field lines, both of which strongly affect basic plasma processes such as thermal conduction. Most knowledge of how astrophysical plasmas behave is based on numerical simulations and modeling. ²

Joseph Larmor first invoked the dynamo mechanism a hundred years ago to explain solar magnetic fields, ³ and theoretical predictions of how the turbulent dynamo should operate go back more than half a century. In 2001 Agris Gailitis and colleagues achieved the first laboratory amplification of a self-exciting magnetic field in a turbulent swirling flow of liquid sodium. ⁴ In 2012 Gregori generated shock waves in a laboratory plasma with a laser and showed that asymmetric shocks, like those occurring in supernovae remnants and gamma-ray bursts, produced seed magnetic fields. ⁵ But the plasma did not reach high enough temperature and velocity to trigger and sustain the dynamo effect. The advent of high-power lasers has now opened a new field of research in which astrophysical environments can be studied in the laboratory.

Galaxy in a lab

At the Omega Laser Facility at the University of Rochester, Tzeferacos and his colleagues irradiated two fixed targets of penny-sized pieces of chlorine-doped polystyrene foil with a series of progressively stronger UV laser pulses to deliver a total of 5 kJ to each target. The foils faced each other 8 mm apart. The laser energy quickly stripped and ionized each foil’s atoms and generated two hot plasma jets directed toward each other. Along the way the jets each passed through a grid of holes. The grids were offset from each other and created interpenetrating fingers of plasma that sheared when they collided and generated a strongly turbulent region. Colliding plasma jets offer a laboratory representation of merging galaxy clusters.

“We’ve tried similar experiments at smaller-scale facilities, but generating plasma conditions where a dynamo can operate was impossible. We needed the power and diagnostics of Omega,” says Tzeferacos. The Omega laser experiments were based on earlier efforts by Tzeferacos, Gregori, and colleagues that used the IR Vulcan laser at the UK’s Rutherford Appleton Laboratory but that did not have sufficient power to achieve dynamo conditions. (See Physics Today, September 2015, page 16 .)

Images taken by an x-ray framing camera showed that the experiments reached the turbulent regime. Inhomogeneities developed in a region more than 1 mm across after the plasma flows collided (see figure 2a). The intensity fluctuations are directly related to electron density fluctuations, which in turn indicate the plasma turbulence. Results from numerical simulations, seen in figure 2b, verify that x-ray images capture the electron density fluctuations expected in a turbulent plasma.

Figure 2.

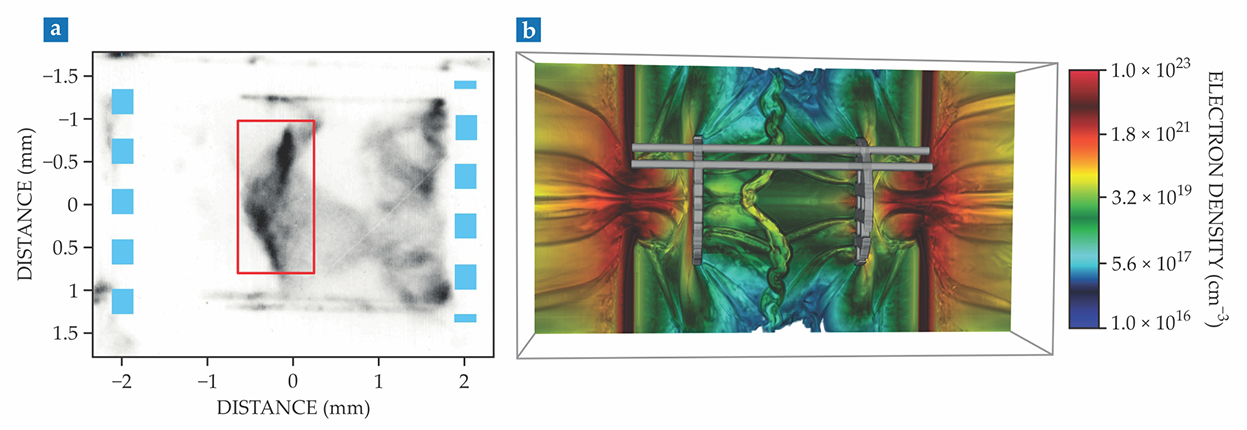
“The big advance was getting the laboratory plasmas to high enough temperature and velocity,” says Christopher Reynolds (University of Cambridge). “We have good simulations, but at the end of the day, lab work is real gas doing real things.”

Measuring magnetism

Tzeferacos and colleagues used numerical simulations to develop two methods for measuring the magnetic field produced by the plasma. Simulations were necessary to determine when to run the diagnostic tools since the experiments lasted tens of nanoseconds, but the strongly amplified magnetic fields persisted for only a fraction of that time.

In one method, the researchers measured the polarization of light passing through the plasma. They based their approach on a technique astronomers use to measure the magnetic fields of distant objects. In the other method, they imaged protons fired through the plasma (figure 3a). Protons are focused into concentrated regions by a magnetic field that bends the protons’ trajectories. By analyzing the concentration of protons, the researchers could reconstruct the magnetic field at the moment the protons were fired through the plasma (see figure 3b).

Figure 3.

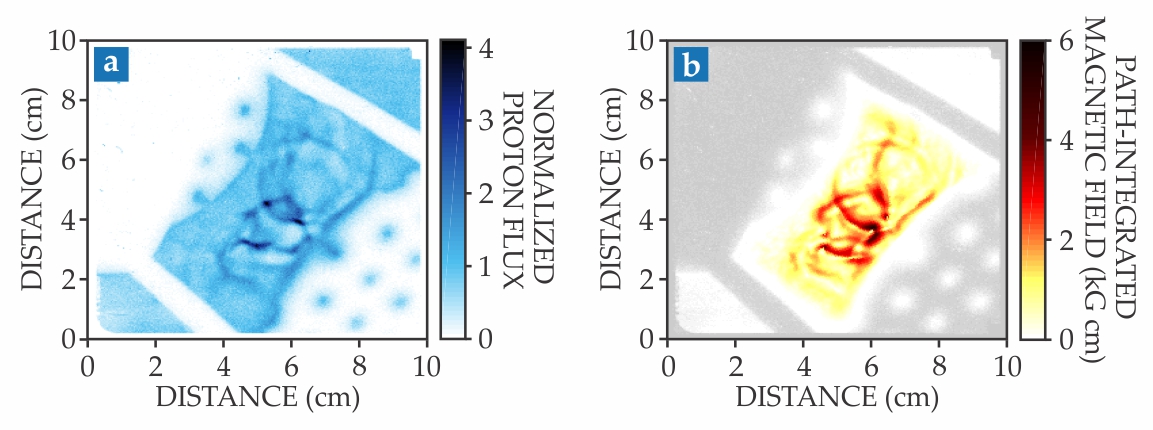
Both methods determined the magnetic field in the turbulent region at several times during the experiment and found that in less than 10 ns, the field amplified by a factor of 25–30. On galactic spatial and temporal scales, the same amplification mechanism could grow a tiny seed field to the observed values.

The initially weak magnetic fields in turbulent dynamo theory evolve according to Maxwell’s equations. When the magnetic field becomes strong enough to deflect the moving plasma, the magnetic energy grows linearly until the plasma motion can no longer amplify the magnetic field. The ratio between magnetic and kinetic energy saturates at a value that depends on the individual fluid properties.

From the lab measurements, the team determined that the magnetic field energy of the plasma saturated at about 4% of its kinetic energy. “It’s reasonable that the mean magnetic energy is quantitatively smaller than the kinetic energy,” says Tzeferacos. Larger and denser plasmas would give the same result, and the measured 4% value is consistent with models in the literature.

Numerical simulations supported the case that the precollision plasmas became primed with tiny seed magnetic fields as a result of density and temperature gradients produced by the laser. ⁶ Simulations also showed that the fields grew exponentially, but the experiments did not temporally resolve the magnetic field growth rate. Follow-up experiments will address the rate at which the magnetic field grows and other, more detailed questions.

From lab to universe

“The fact that the dynamo effect is seen in an experiment validates simulations and provides very strong evidence that this is indeed what happens in the universe at large,” Gregori says. The equations that describe fluids are scale independent—waves in a water glass have the same properties as waves in the ocean.

For magnetic fields, the condition for scale invariance is that the magnetized fluid remains a good conductor. Mathematically, the condition means that a dimensionless parameter called the magnetic Reynolds number R_m is above a critical threshold value of 200. The higher the R_m, the more closely the magnetic field lines move with the plasma. The experiments achieved an R_m of 600, consistent with modeled intergalactic plasmas.

Reynolds observes that “lab work has often not had the prominence it deserves in astrophysics, because it’s difficult to get gases to have meaningful properties. Experiments like this are important for providing fundamental verification of an important theory.”

Atoms in a laboratory plasma frequently collide with each other. That tends to homogenize the plasma, making laboratory plasmas simple to analyze. Unfortunately, the same homogenization does not occur in many less dense astrophysical plasmas, which are harder to understand. However, laboratory plasmas are beginning to approach the collision rate of their astrophysical brethren.

The laboratory platform offers a new opportunity to test theories about magnetic turbulent plasmas in situations relevant to astrophysics, and to analyze how charged particle acceleration develops in a plasma. Future experiments could provide insight into how quickly the magnetic field increases in strength, how strong it can get, and how it alters the turbulence that amplified it.