Hidden order emerges in stream networks

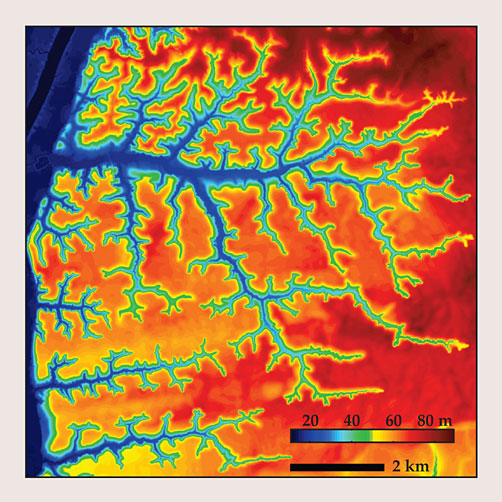
As water drains toward oceans and seas, it slowly carves networks of valleys and channels such as the one shown in figure 1, a topographical map of a stream system that feeds the Apalachicola River near Bristol, Florida. Those so-called drainage networks form in part due to erosion by surface runoff, a process that involves a complex, hard-to-disentangle feedback: Runoff flows shape the topographical landscape, but that landscape also shapes the paths of runoff flow.

Drainage-network formation is also partly due to groundwater flows. Precipitation absorbed by the ground tends to settle into subsurface reservoirs, or aquifers. If an aquifer is pierced by a deep channel—one whose lowest point sits below the water table—then groundwater can seep into the channel and, in the process, erode the channel walls. Known as seepage erosion, that process causes low-lying streams to widen and lengthen over geologic time scales. Because the flow dynamics in aquifers are in most cases independent of the overlying topography, the seepage fluxes are relatively straightforward to model (see the article by Mary Anderson, Physics Today, May 2007, page 42 ). In new work that pairs theory with field observations, an MIT group led by Daniel Rothman has discovered that such seepage flows leave a distinct, and seemingly universal, fingerprint on the complicated patterns seen in many drainage networks. ¹

Branching out

Because rivers and streams form over time spans of millions of years, one can’t observe the growth of natural drainage networks in real time. One challenge the MIT researchers faced, then, was identifying a suitable attribute—some trace of the growth dynamics that’s preserved in the network structure—to use as a benchmark. Says coauthor Olivier Devauchelle, “The difficulty was to find a property that is both unambiguously measurable and theoretically understandable.” “After standing in front of a chalkboard for three months,” recalls coworker Alexander Petroff, “we figured out that we could predict the networks’ branching angles.”

As channels grow due to erosion, they occasionally bifurcate into two branches. Because the channels grow geologically in the upstream direction, those bifurcations are evidenced by the convergence of two streams in the downstream direction. As illustrated in figure 2a, the MIT team modeled a bifurcated channel as a Y-shaped line sink (blue) in an expansive field of groundwater. The sink constantly saps water from the system, so it attracts a steady flow of groundwater from the nearby field. Mimicking the effects of erosion, the tips of the branches grow in the direction from which groundwater enters them—that is, in the direction charted by the two red streamlines. Mathematically, the problem turns out to be nearly identical to diffusion-limited aggregation, the process that gives rise to intricate dendritic patterns in frost formations, mineral deposits, and other systems (see the article by Thomas Halsey, Physics Today, November 2000, page 36 ).

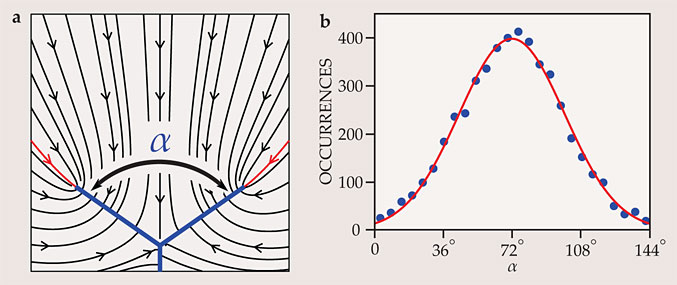
On calculating the flow field as a function of the branching angle α, the group discovered that α = 2π/5 radians, or 72°, has a special quality: If α is larger, the streamlines curve in a way that causes the arms to bend inward, and if α is smaller, they cause the arms to bend apart; but if α = 2π/5, the branches grow straight at a perfectly fixed angle. What’s more, because the relevant dynamics are scale invariant and independent of the flow parameters, the predicted angle should be found at any branch in any seepage network.

The Bristol network is in many ways a perfect system against which to test the theory. Lying on deltaic sediments 40 miles inland from the Gulf of Mexico, it occupies a sandy terrain that readily absorbs precipitation. As a result, there’s no appreciable surface runoff, and one can safely assume that the stream network was carved out entirely via seepage erosion. Indeed, as shown in figure 2b, a histogram of the actual α values observed in the network is well described by a Gaussian distribution with mean 71.9° ± 0.8°. A popular alternative theory—that the natural branching angle is the one that yields the least stress on the channel walls—would have predicted a characteristic branching angle of 90°.

The researchers can’t yet explain the distribution’s large standard deviation, nearly 28°, but they suspect it may be attributable to heterogeneities in the landscape or to stream–stream interactions that aren’t accounted for in the model. “The real system is not just a pristine set of channels growing in a groundwater field. There are fallen trees, there’s vegetation and mud everywhere—it’s a total mess,” explains Rothman. “The surprise is that the model worked as well as it did.”