Gravity Probe B concludes its 50-year quest

In 1962 Francis Everitt arrived at Stanford University as the first full-time staff member of Gravity Probe B (GP-B), a satellite-borne experiment conceived to test Albert Einstein’s general theory of relativity. A half century and $760 million later, Everitt announced at a NASA press conference in May, seven years after launch, that GP-B had completed its data analysis and Einstein’s magnum opus passed comfortably. ¹

If the experiment had run to spec, it would have measured with unprecedented precision two properties predicted by general relativity: the so-called geodetic and frame-dragging effects, which imply that an orbiting gyroscope will precess even when no external torque acts on it. Though Everitt and colleagues were able to confirm the geodetic effect with an impressive and currently standard-bearing error of 0.3%, they could only confirm frame dragging—a much smaller effect less well measured by independent efforts—to within 20%. Nonetheless, GP-B’s half-century-long experiment was a remarkable odyssey that included the fabrication of gyroscopes the size of Ping-Pong balls, now included in Guinness World Records as the most perfectly spherical objects ever made, and a five-year effort to understand some strange things those gyros did while GP-B was collecting data.

What’s the point?

In the Newtonian world, a mass exerts a gravitational force on other masses. The general-relativistic description is rather different. In Einstein’s view, energy and momentum influence the geometry of spacetime, and geometry—not force per se—determines motion.

The geodetic effect arises in the presence of any mass, but frame dragging comes about only when the spacetime-distorting mass is itself spinning. To understand the two effects in the violent environment of two spinning black holes, you’d need the full machinery of general relativity. But in the vicinity of Earth, where gravity is relatively weak, you can intuitively grasp much of what’s going on by appealing to electromagnetic analogues. The geodetic effect can, in part, be understood as the gravitational analogue of the spin–orbit coupling familiar from atomic physics. A spinning electron orbiting in the Coulomb field of a nucleus sees a magnetic field that exerts a torque on it. Likewise, a gyroscope orbiting Earth sees a magnetic-like field that exerts a torque on it. That analogue field accounts for one-third of the geodetic precession.

The remaining two-thirds is intimately tied to the curvature of space; you can realize the effect with a needle and a globe. Start with the needle at the North Pole. Point it south along the prime meridian and drag it tangent to the globe down to the equator. Then drag the needle west along the equator to the 90° W meridian, keeping it pointed south. Return to the pole along the 90° W meridian and when the needle arrives, you’ll see that it is pointing perpendicular to the direction you chose at the start: In the course of its roundtrip, the needle precesses by 90°.

The four GP-B gyroscopes orbiting Earth saw not only a torque-exerting, magnetic-like field by virtue of their orbital motion but also a magnetic-like field created by the revolution of the planet itself. That second field is the source of the frame-dragging effect measured by the experiment. As a consequence of the effect, a freely falling object outside Earth tends to rotate along with Earth—that is what is meant by “frame dragging.” The planet rotates relatively slowly, and the frame-dragging effect is minute at the location of the GP-B satellite. But the dragging is nonetheless predicted to be there and to be measurable.

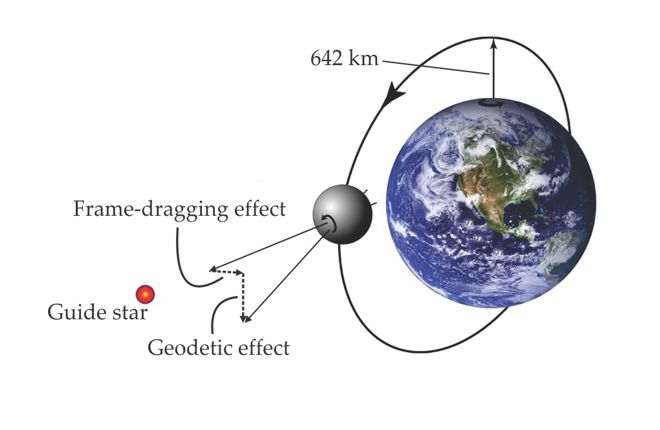
The geodetic and frame-dragging effects act differently on a gyroscope orbiting Earth. The GP-B team exploited that difference by having the gyroscope-carrying spacecraft orbit in a polar plane. As figure 1 shows, the small changes in a gyroscope’s spin vector predicted by the two effects are then perpendicular to each other. Thus GP-B had the capability to tease out independent measurements of geodetic and frame-dragging precession.

Four balls

In a technical memo written for the Institute for Defense Analyses in 1959, MIT physicist George Pugh suggested that general relativity could be tested with a gyroscope orbiting in a satellite free of atmospheric drag, and he gave rough values for the precession due to the geodetic and frame-dragging effects. A few months later Stanford’s Leonard Schiff properly worked out the numbers and, with colleagues William Fairbank and Robert Cannon, began what would eventually become the GP-B collaboration.

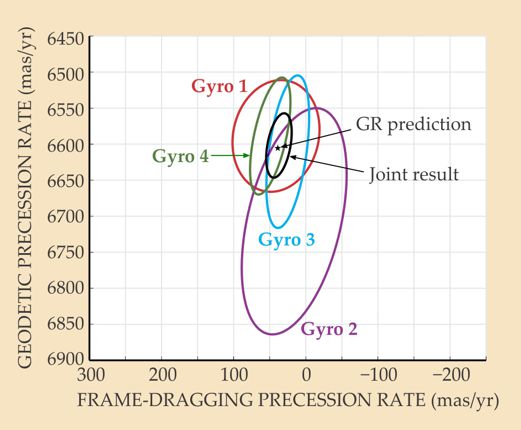
The spacecraft housing the experiment was launched in April 2004. Data collection began in August and continued for about a year. At the NASA press conference, Everitt announced a geodetic precession rate of 6602 ± 18 milliarcseconds/year and a frame-dragging rate of 37.2 ± 7.2 mas/yr. The general-relativistic predictions are, respectively, 6606 mas/yr and 39.2 mas/yr. Figure 2 shows the results obtained for each of GP-B’s four gyroscopes along with the combined result.

The heart of the GP-B experiment was a fused silica structure containing the four gyroscopes (for redundancy) and a beautiful telescope much like the one shown in figure 3. The gyroscopes are remarkably spherical: If they were blown up to Earth size, the tallest mountain would be 3 meters high. That’s essential, lest Newtonian torques overwhelm the relativistic effects GP-B planned to measure. Helium gas gave the gyroscopes their spin, which was initially aligned with the telescope axis. The telescope remained pointed at a guide star, providing a reference direction against which the evolving gyroscopic spin could be compared. The spacecraft itself rolled around the telescope axis with a period of about 80 seconds; that rotation helped average out stray Newtonian torques and other annoyances.

It is the physics of superconductivity that allowed the GP-B team to monitor the spin precession of the featureless, almost perfectly spherical gyroscopes. Each gyro was covered with a very thin layer of niobium and cooled with superfluid helium to 1.8 K. Once the gyros were set spinning, the positive charges in the superconductor’s lattice produced a magnetic dipole field whose axis was parallel to the gyro spin axis. That field could be tracked with a superconducting quantum interference device (SQUID).

Stray charge and straying gyros

The GP-B collaboration overcame numerous hurdles in the course of the experiment: The SQUID calibration proved to be subtle; the proper motion of the guide star needed to be carefully measured; the superfluid He wanted to escape from its dewar flask; and even at an altitude of 642 km, Earth has a tenuous atmosphere that drags the spaceship. That last problem was ingeniously solved by shunting evaporated He to microthrusters that compensated for atmospheric drag with puffs of gas only one-hundredth as forceful as a human breath.

But one difficulty, though anticipated, was severely underestimated and made the uncertainties larger than foreseen: stray patches of static charge on the gyroscopes and their housing. Spherical as they were, the GP-B gyros were not perfect. Consequently the spin axes of the gyros were not perfectly aligned with the gyros’ axes of maximum-moment of inertia. That misalignment enabled the patch charges to exert unwanted torques on the gyros.

The severity of the problem was revealed only after the data had been collected. During 46 days of subsequent calibration runs, the GP-B experimenters deliberately misaligned the spacecraft’s roll axis and the spin axis of the gyroscopes to enhance the torques exerted by the surface charges. Extrapolating back to the experimental conditions, they found that the misalignment torques were 100 times as large as had been expected.

The post-calibration analysis also revealed a dramatic manifestation of the surface charge, a behavior that had remained hidden to the GP-B team before the calibration runs: Every so often—apparently at random—the spin axis of a gyroscope would migrate by tens of milliarcseconds over the course of a day. In fact, the migration was not random: It was a resonance phenomenon that occurred only when the slowly varying period for the precession of the gyroscope’s moment-of-inertia axes about its spin axis was an integral multiple of the spacecraft’s roll period.

For more than five years after collecting the data, the GP-B scientists struggled to understand and model the distribution of the charge patches and the effects caused by those charges. Once they imposed the corrections implied by their complicated model, the data from the four gyros were seen to be mutually consistent, as shown in figure 2. The cost of all that complexity is the large error bars in the GP-B results.

Not as easy as it sounds

Everitt and company had hoped to measure the geodetic precession to an accuracy of 0.01% and the frame-dragging precession to 1%. Had they succeeded, they would have achieved by far the most precise tests of those general-relativistic effects. However, as early as 1996, lunar-ranging data had confirmed the geodetic effect to 0.7%, and improved lunar-ranging experiments are currently under way. In 2004, just after GP-B began taking data, Ignazio Ciufolini and Erricos Pavlis announced the results of their laser-ranging experiments on two artificial LAGEOS satellites. They reported confirming the frame-dragging effect to 10%, but they had to assume a priori the correctness of the general-relativistic geodetic effect. A third satellite, the Italian Space Agency’s LARES, is scheduled for launch later this year. It may enable an order-of-magnitude improvement in the precision with which frame dragging can be tested.

Fairbank remarked early on, “No mission could be simpler than GP-B: It’s just a star, a telescope, and a spinning sphere.” But conceptual simplicity is no guarantee that a cutting-edge experiment will come off as anticipated. “Did I have the slightest idea,” muses Everitt, “that it was going to take 50 years? No. If I had known it would be 50 years, would I have done it? Probably not. But one has never been bored.”