From quantum cheating to quantum security

Cryptography—the art of code-making—has a long history of military and diplomatic applications, dating back to the Babylonians. In World War II, the Allies’ feat of breaking the legendary German code Enigma contributed greatly to their final victory. Nowadays, cryptography is becoming increasingly important in commercial applications for electronic business. Sensitive data such as credit card numbers and personal identification numbers (PINs) are routinely transmitted in encrypted form. Quantum mechanics is a new tool for both code-breakers and code-makers in their eternal arms race. It has the potential to revolutionize cryptography both by creating perfectly secure codes and by breaking standard encryption schemes.

The best-known application of cryptography is secure communication, ¹ illustrated in figure 1. Suppose Alice would like to send a message to Bob, but there is an eavesdropper, Eve, who is wiretapping the channel. To prevent Eve from knowing the message, Alice may perform encryption—that is, transform the message to something that is unintelligible to Eve—during the communication. On receiving the message, Bob inverts the transformation and recovers the message.

Figure 1.

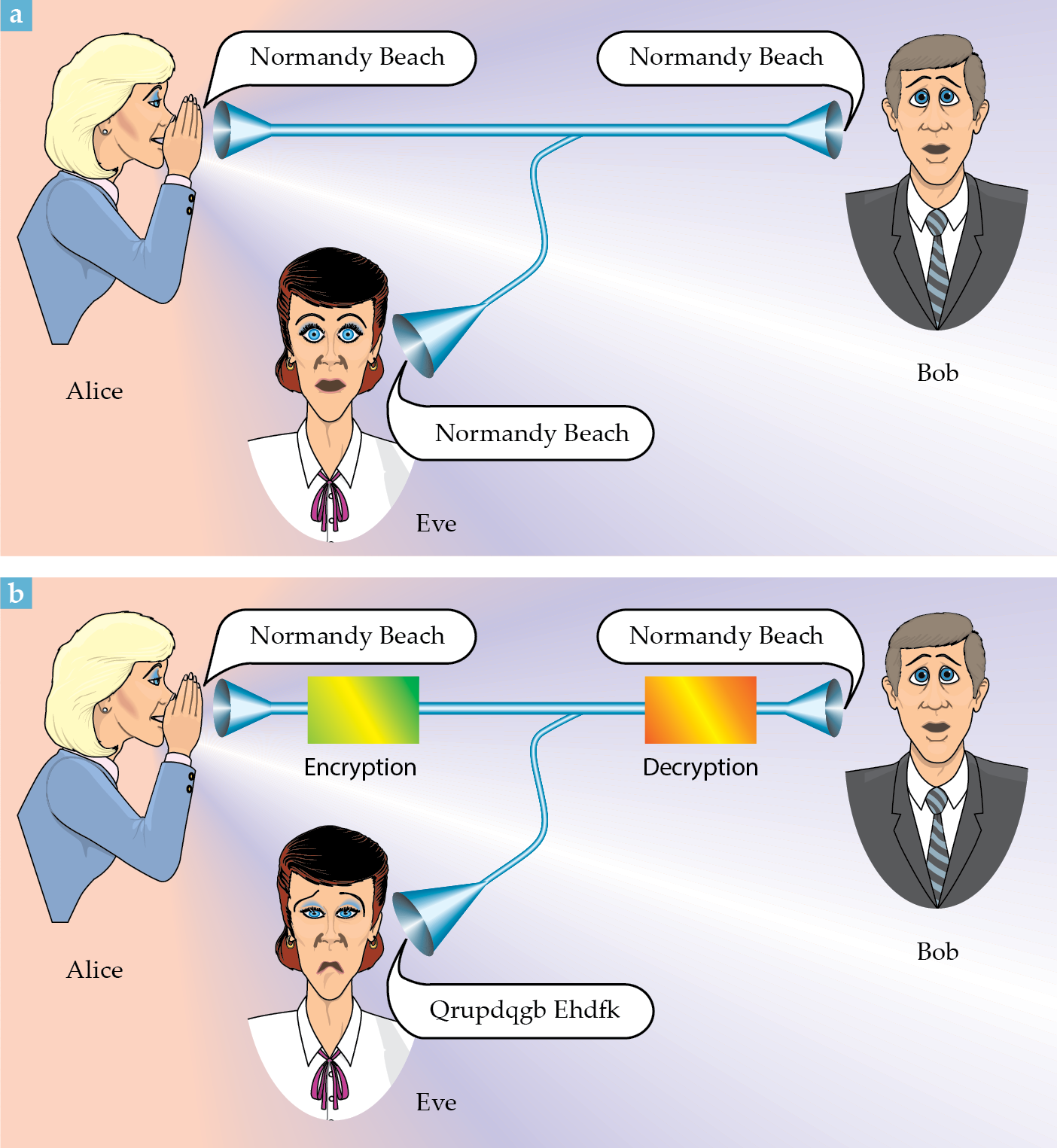
Bob’s advantage over Eve lies in his knowledge of a secret, commonly called the key, that he shares with Alice. The key tells him how to decode the message. Consider this example (in the style of Cold War espionage thrillers):

Blond is using a perfectly unbreakable cipher, a “one-time pad.” The secret codebook allows N and Blond to share a long secret binary string—the key—before Blond leaves on his mission. Whenever N would like to send a message to Blond, she first converts it to binary. She then takes the exclusive-OR (XOR) between each bit of the message and the corresponding key bit to generate the encrypted message, which is transmitted over a public channel. An enemy can intercept the encrypted message, but without the key, it is incomprehensible gibberish, offering no clue to the contents of the original message. On the other hand, Blond, by looking up the key in the codebook, can recover the original message by taking the XOR between the encrypted message and the key. Blond immediately burns the used page of the codebook to prevent it from falling into enemy hands in the future.

Key distribution problem

R was serious for a good reason. The reuse of keys by the Soviet Union (due to the manufacturer’s accidental duplication of one-time pad pages) enabled US cryptanalysts to unmask the atomic spy Klaus Fuchs in 1949. ² When the key for a one-time pad is used more than once, enemy cryptanalysts have the opportunity to look for patterns in the encrypted messages that might reveal the key. Nevertheless, excellent cryptosystems (known as symmetric cryptosystems) that reuse the key have been developed. The longer the key, the more secure the system. For instance, a widely used system is the Data Encryption Standard (DES), which has a key length of 56 bits. No method substantially more efficient than trying all 2⁵⁶ values of the key is known for breaking DES. It is still conceivable, however, that some yet unknown clever algorithm could defeat DES and its cousins.

For top-secret applications, therefore, the one-time pad is preferable. Blond’s predicament illustrates the drawback of the one-time pad: When the secret key is used up, the code cannot be used until the sender and receiver get together to share a new secret key. Sending a courier with a new codebook into the Prague Spring is a dangerous and unreliable business. Even if the courier arrives, Blond and N can never be sure that the codebook was not copied during its journey.

This issue is known as the “key distribution problem.” A possible solution is public key cryptography. Instead of a single long key shared between the sender and receiver, public key cryptography uses two sorts of keys: one public key, which is known to the world, and one private key, known only to the receiver. Anyone with the public key can send secret messages, but only someone who knows the private key can read them. The important defining feature of public key cryptography is that, even knowing the encryption key, there is no known computationally efficient way of working out what the decryption key really is. As an example, the security of the best-known public key cryptosystem, RSA, relies on the difficulty of factoring large integers (see figure 2).

Figure 2.

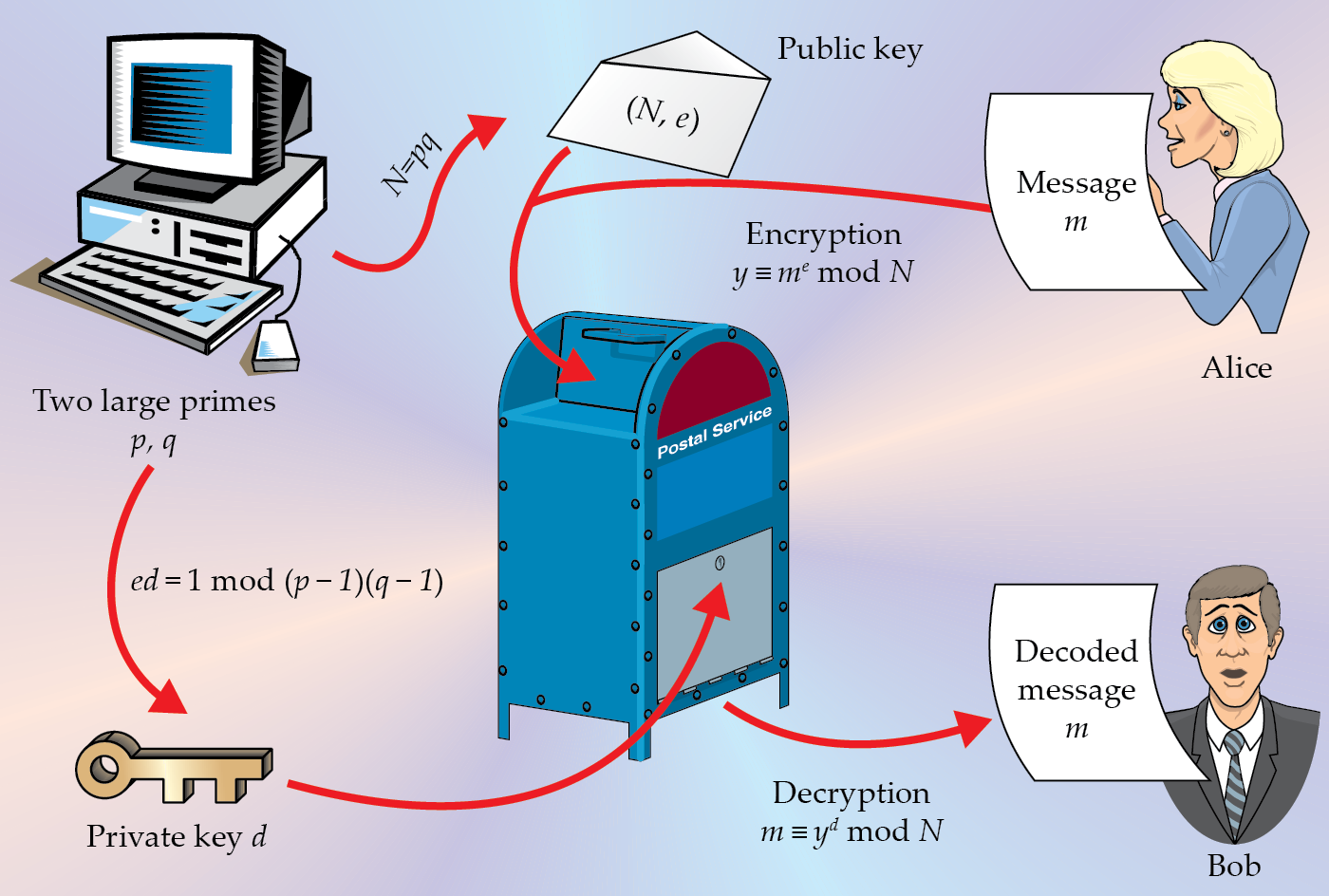
Public key cryptography can be used for another important task: digital signatures. A digital signature exchanges the role of the keys used in public key cryptography: The private key is used to generate a signature and the public key is used to verify it. Only someone with the private key could have created the signature.

Quantum code-breaking

Both DES and RSA rely on an unproven assumption: There is no fast algorithm to determine the secret key. For instance, RSA is believed to be secure because mathematicians throughout the world have worked very hard to break it, steadily producing modest improvements in factoring algorithms, but without groundbreaking success. With only modest increases in key size, users of RSA can easily keep ahead even of the exponential growth in computing power over the years.

Quantum mechanics changed this. In 1994, Peter Shor of AT&T Laboratories invented a quantum algorithm for efficient factoring of large numbers. ³ The state of a quantum computer is a superposition of exponentially many basis states, each of which corresponds to a state of a classical computer of the same size. By taking advantage of interference and entanglement in this system, a quantum computer can perform in a reasonable time some tasks that would take ridiculously long on a classical computer. Shor’s discovery propelled the then-obscure subject of quantum computing into a dynamic and rapidly developing field, and stimulated scores of experiments and proposals aimed toward building quantum computers.

Another remarkable discovery was made by Lov Grover of Bell Laboratories, Lucent Technologies, who in 1996 invented a quantum searching algorithm ⁴ (see Physics Today, October 1997, page 19 ). To find one particular item among $N$ objects requires checking $O(N)$ items classically. With Grover’s algorithm, a quantum computer need only look up items $O(\sqrt{N})$ times. It can be used to radically speed up the exhaustive key search of DES (that is, trying all 2⁵⁶ possibilities).

If a quantum computer is ever constructed in the future, much of conventional cryptography will fall apart! To provide the same security, the key lengths of symmetric schemes like DES would have to be doubled due to Grover’s algorithm. The most commonly used public key schemes are RSA and others based on discrete logarithms or elliptic curves; Shor’s algorithm breaks all of them. Even if it is decades until a sufficiently large quantum computer can be built, this is a matter of current concern: Some data, such as nuclear weapons designs, will still need to remain secret, and it is important that today’s secret messages cannot be decoded tomorrow.

Quantum code-making

Even if DES and RSA do fall apart, the one-time pad remains a perfectly unbreakable cipher even against a quantum computer. However, as previously discussed, it has a serious catch: the key distribution problem. It presupposes that Alice and Bob share a key that is secret and as long as the message. There is no way to guarantee that in practice. Trusted couriers can be bribed or even intercepted without their knowledge. More generally, classical signals are distinguishable. An eavesdropper can reliably read the signals without changing them. Therefore, in classical physics there is nothing, in principle, to prevent an eavesdropper from wiretapping the key distribution channel passively.

Fortunately, quantum mechanics helps to make codes as well as break them. ⁵ (See also Charles Bennett’s article, “Quantum information and computation ,” Physics Today, October 1995, page 24.) The Heisenberg uncertainty principle dictates that it is fundamentally impossible to know the exact values of complementary variables such as a particle’s momentum and its position. This apparent limitation imposed by quantum mechanics can be a powerful tool in catching eavesdroppers. The central idea is to use nonorthogonal quantum states to encode information. More concretely, the essence of quantum cryptography can be understood in a single question: Given a single photon in one of four possible polarizations (↔, ↕, ⤢, or ⤡), can one determine its polarization with certainty? Surprisingly, the answer is no. The rectilinear basis (↔ and ↕) and the diagonal basis (⤢ and ⤡) are incompatible, so the Heisenberg uncertainty principle forbids us from simultaneously measuring both. More generally, experiments distinguishing nonorthogonal states, even if only partially reliable, will disturb the states.

The key distribution problem can be partially solved by quantum mechanics using the idea of quantum key distribution (QKD). The first and best-known protocol, usually called “BB84” because it was published in 1984 by Charles Bennett and Gilles Brassard, ⁶ is described in the box. In a prototypical QKD protocol, Alice sends some nonorthogonal quantum states to Bob, who makes some measurements. Then, by talking on the phone (which need not be secure), they decide if Eve has tampered with the quantum states. If not, they have a shared key that is guaranteed to be secret. Note that Alice and Bob must share some authentication information to begin with; otherwise, Bob has no way to know that the person on the phone is really Alice, and not a clever mimic. The key generated by QKD can subsequently be used for both encryption and authentication, thus achieving two major goals in cryptography.

Experimental QKD

QKD is an active experimental subject. The first working prototype, constructed in 1989 at IBM in Yorktown Heights, New York, transmitted quantum signals over 32 cm of open air. ⁷ Since then, various groups—including those led by Paul Townsend at the British Telecommunications Photonics Technology Research Centre (now part of Corning), Jim Franson of Johns Hopkins University, Nicolas Gisin and Hugo Zbinden of the University of Geneva, and Richard Hughes of Los Alamos National Laboratory—have made important contributions. A primary focus has been a series of impressive experiments over commercial optical fibers. 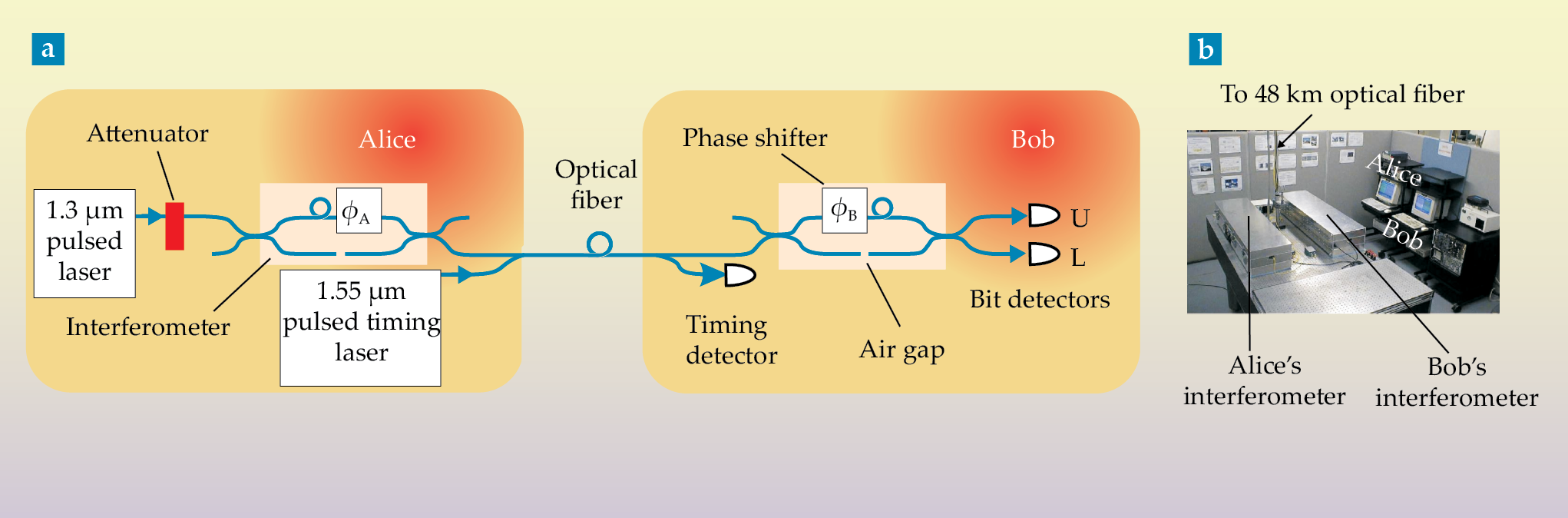The world record distance for QKD, ⁸ at the time of writing, is about 50 km. One of the long-distance experiments, performed at Los Alamos, is depicted in figure 3.

Figure 3.

Most experiments to date have used variants of either the BB84 or B92 schemes (see the box), although recently three groups—one led by Paul Kwiat of Los Alamos, Gisin and Zbinden’s group at Geneva, and a collaboration led by Anton Zeilinger of the University of Vienna and Harald Weinfurter of the University of Munich—have independently implemented protocols based on entangled pairs of particles, also known as Einstein-Podolsky-Rosen or EPR states. In the BB84 and B92 schemes, typically a single-photon source is simulated using attenuated coherent states—on average, only a fraction of a photon is actually sent. With additional losses in the fiber, very few arriving laser pulses actually contain a photon. This low yield does not interfere much with key distribution, however, since only the photons that reach Bob are used in the protocol. The key is generally encoded in either the polarization or the phase of the photon. Error rates in the photons actually received are usually a few percent.

For commercial applications in, say, a local area network environment, it is useful for a quantum cryptographic system to be integrated into a passive multiuser optical fiber network and its equipment to be miniaturized. Townsend’s group has done much work in this area. ⁹ For point-to-point applications, the Geneva group has devised a so-called “plug and play” system that automatically compensates for polarization fluctuations. ¹⁰ Such systems might someday convey secret information between government agencies around Washington, DC, or connect bank branches within a city.

QKD has also been performed in open air, ¹¹ during daylight, with a current range of about 1.6 km. Ambitious schemes to perform a ground-to-satellite QKD experiment have been proposed. If successful, quantum cryptography may be used to ensure the security of command control of satellites from control centers on the ground.

Future experiments will aim to make QKD more reliable, to integrate it with today’s communications infrastructure, and to increase the distance and rate of key generation. Another ambitious goal is to produce a quantum repeater using techniques of quantum error correction. Such an accomplishment will require substantial technical breakthroughs, but would allow key distribution over arbitrarily long distances.

Is QKD secure?

While experiments in QKD forged ahead, the theory developed more slowly. A clever Eve can adopt many possible strategies to fool Alice and Bob, including subtle quantum attacks entangling all of the particles sent by Alice. Taking all possibilities into account, as well as the effects of realistic imperfections in Alice and Bob’s apparatus and channel, has been difficult. A long series of partial results has appeared over the years, addressing restricted sets of strategies by Eve, ¹² but only in the past few years have complete proofs appeared.

One class of proofs, by Dominic Mayers ¹³ and subsequently by others, including Eli Biham and collaborators and Michael Ben-Or, ¹⁴ attacks the problem directly and proves that the standard BB84 protocol is secure. Another approach, by one of us (HKL) and H. F. Chau, ¹⁵ proves the security of a new QKD protocol that uses quantum error-correcting codes. ⁵ (For more on quantum error correction, see John Preskill, “Battling decoherence: The fault-tolerant quantum computer ,” Physics Today, June 1999, page 24.) This approach allows one to apply classical probability theory to tackle a quantum problem directly. It works because the relevant observables all commute with each other. While conceptually simpler, this protocol requires a quantum computer to implement. The two approaches have been unified by Peter Shor and John Preskill, ¹⁶ who showed that a quantum error-correcting protocol could be modified to become BB84 without compromising its security.

The proof of the security of QKD is a fine theoretical result, but it does not mean that a real QKD system would be secure. ¹⁷ Some known and unknown security loopholes might prove to be fatal. Apparently minor quirks of a system can sometimes provide a lever for an eavesdropper to break the encryption. For instance, instead of producing a single photon, a laser may produce two; Eve can keep one and give the other to Bob. She can then learn what polarization Alice sent without revealing her presence. There are various possible solutions to this particular problem; it is the unanticipated flaws that present the greatest security hazard. Ultimately, we cannot have confidence that a real-life quantum cryptographic system is secure until it has withstood attacks from determined real-life adversaries. Traditionally, breaking cryptographic protocols has been considered to be as important as making them—the protocols that survive are more likely to be truly secure. The same standard will have to be applied to QKD.

Post–Cold War applications

There are many problems beyond secure communication that can be addressed by cryptography.

This dating problem can be phrased as the problem of computing a function f(a, b) = ab, where a and b are single bits held respectively by Alice and Bob (0 = not interested, 1 = interested). Problems like this can be solved classically using variants of public key cryptography, which we know might be rendered insecure by quantum computers. By exchanging quantum states, can Alice and Bob solve the above dating problem with absolute security?

There are many possible functions f that two people might wish to compute together, too many to consider each of them individually. Instead, cryptographers rely on a suite of primitive operations that can be combined to build more complex functions. One important protocol is called bit commitment, and it is the electronic equivalent of a locked box. Alice chooses a bit, 0 or 1, and writes it on a piece of paper, which she deposits in the box. She gives the box to Bob but keeps the key. She cannot change what she wrote, and without the key, Bob cannot open the box. But at some later point, Alice can give Bob the key and reveal her bit. By itself, bit commitment is useful mostly for debunking professional psychics, but it serves as a useful building block for more interesting functions.

Consider the following bit commitment scheme ⁶ proposed by Bennett and Brassard: If Alice wishes to commit to a 0, she sends Bob a polarized photon in the rectilinear basis; if she wishes to commit to a 1, she sends Bob a polarized photon in the diagonal basis. In either case, Alice flips a coin to decide which of the two polarizations to send. Bob has no way to tell which basis Alice used; no matter which bases Alice and he choose, Bob would measure a random value. But when Alice unveils her bit, telling Bob which of the four states she sent, Bob can measure in the appropriate basis to verify that Alice is telling the truth. If she lies about which basis she used, Bob has a 50% chance of finding out. If the protocol is repeated many times, Alice’s chance of successfully cheating is abysmally small.

This protocol is secure against a classical cheater, who does not have much ability to store and manipulate quantum states. But as Bennett and Brassard recognized, a quantum cheater can break the protocol. Suppose that instead of picking a specific state and sending it to Bob, Alice creates an entangled pair of photons, (|↔↕⟩ − |↕↔⟩)/√2 (an EPR pair), and sends the second photon to Bob, keeping the first one. She stores the quantum state of the first photon and delays measuring it. Suppose that when the time comes for Alice to open the commitment, she decides she would like the committed bit to read 0, which requires her to specify a state in the rectilinear basis. Because of the entanglement, Alice knows that if she and Bob measure in the same basis, they will get opposite results. Therefore, she can measure her photon in the rectilinear basis and tell Bob he has the opposite polarization, and she will always be right.

If Alice instead wishes the committed bit to read 1, she needs a state in the diagonal basis. But (|↔↕⟩ − |↕↔⟩)/√2 ≡ (|⤢⤡⟩ − |⤡⤢⟩)/√2. So Alice can measure her particle in the diagonal basis and again be sure that Bob’s measurement outcome will be opposite to hers. Quantum cheating allows Alice to change her mind at the last minute without being caught by Bob, thus totally defeating the purpose of bit commitment.

Nonetheless, more sophisticated schemes for quantum bit commitment were proposed, and for a long time were believed to be secure. Eventually, the bubble burst and it was shown that the above quantum cheating strategy, which uses EPR nonlocality and delayed measurements, can be generalized to break all two-party quantum bit commitment schemes. ¹⁸ If Alice and Bob hold one of two pure quantum states that are indistinguishable to Bob, then Alice, acting unilaterally, can change one to the other. Therefore, the two basic requirements of bit commitment—that Bob does not know the bit and that Alice cannot change it—are fundamentally incompatible with quantum mechanics.

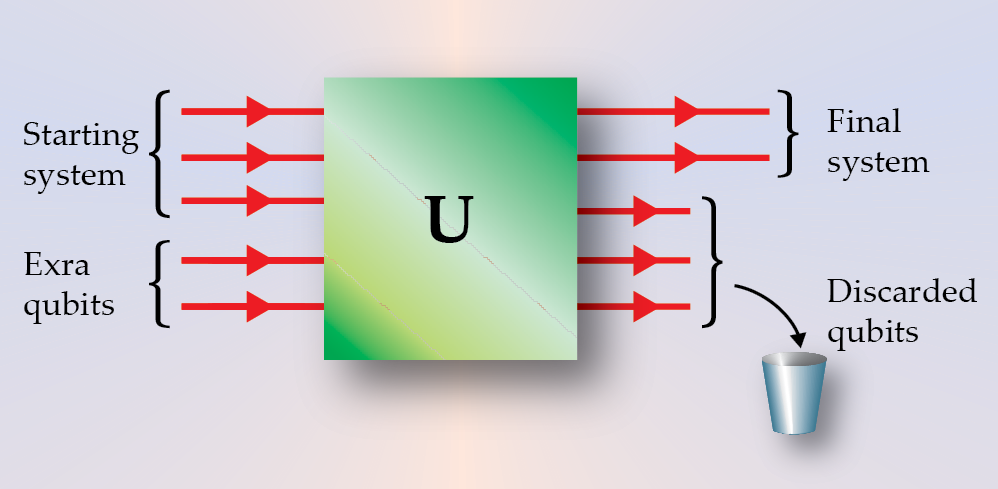
The strength of the proof lies in its generality. The idea is to treat the whole system as if it were quantum mechanical, extending the part that was originally quantum to include any dice, measuring devices, and classical computations that appear in the protocol. From this point of view, the original protocol is equivalent to a purely quantum one, with some of the output being thrown in the trash (see figure 4). Note that throwing something away can never help a cheater, so we might as well assume that the state shared by Alice and Bob is the pure quantum state that is completely determined by the protocol. That assumption substantially reduces the complexity of the problem. It is not difficult to show that when Alice and Bob hold a pure state, quantum bit commitment is impossible.

Figure 4.

Following the fall of quantum bit commitment, other important basic quantum cryptographic protocols have also been proven to be insecure by one of us (HKL), thus leaving the field in a shambles. What is left?

Some potential applications in cryptography are too similar to bit commitment and cannot be done at all quantum mechanically. Others have more modest goals and can be solved by quantum protocols. For instance, Lior Goldenberg, Lev Vaidman, and Stephen Wiesner of Tel Aviv University have proposed a method of “quantum gambling,” in which a cheater must pay a large fine if caught. The majority lie in a middle ground—we do not know whether they can be solved. The dating problem is an example. Many approaches to it tread too near bit commitment and are doomed to failure, but it’s possible there are others, as yet undiscovered, that do not.

Physics today, cryptology tomorrow

Quantum computers are still on the drawing boards, and quantum cryptographic systems are only prototypes. Still, there are a number of reasons for thinking about quantum cryptology today. Unlike other cryptosystems, the security of QKD is based on fundamental principles of quantum mechanics, rather than unproven computational assumptions. QKD eliminates the great threat of unanticipated advances in algorithms and hardware breaking a widely used cryptosystem. Small-scale QKD systems are well within the capabilities of today’s technology, and commercial systems could be available within a few years (although whether such systems are widely adopted depends on many nonacademic factors, including cost).

Furthermore, grappling with the problems posed by quantum protocols can give us insight into more general questions about quantum mechanical systems in many fields of physics. For instance, one reason it is hard to analyze protocols and attacks is that they frequently involve a combination of quantum and classical behaviors. In considering bit commitment, though, it was possible to replace classical parts of the protocol with a quantum description, an approach that is useful for many problems inside and outside the field of quantum cryptography. This fully quantum treatment is sometimes called the Church of the Larger Hilbert Space, following John Smolin of IBM. All quantum operations, including measurements, are unitary when considered as acting on a larger Hilbert space (figure 4).

Finally, quantum mechanics changes the world of cryptology, and it is important to know what the new terrain will look like to decide on cryptographic standards that may last for decades. In a world where quantum computers and communication are commonplace, today’s most widespread public key cryptosystems would no longer work; in the worst case, perhaps no public key cryptosystem will work. If so, symmetric cryptosystems and QKD would partially fill the gap, allowing secure communication. Unfortunately, digital signatures would fail as well, meaning important communications would need to be notarized by a trusted third party.

Of course, QKD and symmetric cryptosystems are not useful in situations in which Alice and Bob have never met. Solving this problem would probably require a quantum cryptographic center, which could verify the identity of both of them. The center would have to be known and trusted by both Alice and Bob.

Problems beyond secret communication and digital signatures are a mixed bag. Many, such as bit commitment and perhaps the dating problem, would be impossible, whereas others, such as quantum gambling, could be carried out with complete security.

This is just one of a number of possible futures. Perhaps some new or existing public key cryptosystems will survive quantum computation, or perhaps new public key systems will be developed that can only run on a quantum computer. Perhaps quantum computers will always remain difficult to build (we believe that this is unlikely), and public key cryptography will remain widespread, despite its potential flaws. Only time will tell who benefits more from quantum cryptology: the code-makers or the code-breakers.