Exotic chimera dynamics glimpsed in experiments

In Greek mythology, a chimera is a three-headed, fire-breathing monster—part lion, part goat, part serpent. In the parlance of nonlinear dynamics, the term “chimera state” refers to a similarly incongruent beast—a partly synchronized, partly incoherent system of coupled oscillators. It’s been shown, in theory at least, that chimera states can exist, but they’ve proved difficult to spot in the real world. Now they’ve made their laboratory debut in a pair of nearly simultaneous experiments—one led by Rajarshi Roy at the University of Maryland, College Park, ¹ the other by Kenneth Showalter at West Virginia University. ²

The odd couple

Oscillators, objects that exhibit cyclic behavior, are commonplace. They include AC circuits, fireflies, and neurons, to name just a few. When several oscillators are coupled, they often synchronize: Fireflies can flash in concert; cardiac pacemaker cells fire in unison, resulting in a regular heartbeat. Indeed, spontaneous synchronization occurs in any number of natural and artificial systems.

In the 1970s, mathematician Yoshiki Kuramoto began developing the formalism that would explain how synchronization can come about via global coupling. ³ Take fireflies, for example. The Kuramoto model assumes that each firefly is coupled to every other firefly in the group—that is, each firefly continually adjusts its own firing frequency and phase toward the mean frequency and phase of the group. The model admits two possible outcomes: Below some threshold coupling strength, the fireflies flash incoherently; above it, the group begins to synchronize.

One can also imagine a scenario in which each firefly sees just a fraction of the others or is coupled more strongly to nearby fireflies than to distant ones. As recently as a decade ago, that scenario—known as nonlocal coupling—had gone largely ignored. Theorists preferred to work on the more tractable problems of global coupling and of local coupling, in which each oscillator interacts only with its adjacent neighbors.

In 2002, however, Kuramoto and collaborator Dorjsuren Battogtokh discovered that nonlocal coupling could produce patterns that weren’t seen in globally or locally coupled systems. Their numerical simulations revealed one particularly puzzling behavior: Under certain conditions, oscillators organized into coexisting synchronous and asynchronous domains. Two years later Cornell University’s Steven Strogatz and student Daniel Abrams (now at Northwestern University) showed analytically that the new state—which they termed the chimera state—was long-lived and dynamically stable. ⁴

In Strogatz and Abrams’s model, as in Kuramoto and Battogtokh’s, the oscillators that make up the chimera state are identical and governed by identical coupling rules. There’s no way to predict a priori whether an oscillator will end up in a synchronous or asynchronous domain. On its face, the behavior resembles spontaneous symmetry breaking. But symmetry breaking generally occurs by way of a second-order phase transition. For instance, as a ferromagnetic melt cools below a critical temperature, the isotropic state becomes unstable, and spins must choose an alignment. As Strogatz and Abrams discovered, chimera states don’t require such a transition; they can form even when the uniform state is also stable.

Chimera states bear close resemblance to so-called bump states in neural networks, in which a subset of neurons fires in sync while others fire incoherently, and to unihemispheric sleep, the ability of some birds and dolphins to sleep with one half of their brain while the other half remains aware. The new experiments, however, mark the first time that physical systems have been conclusively demonstrated to host chimera states.

An optical chimera

The Maryland experiment grew out of a serendipitous encounter between Roy and Iryna Omelchenko of the Technical University of Berlin. Omelchenko, Eckehard Schöll, and coworkers had been developing a theoretical model of chimera states, and Roy figured that he and University of Maryland coworkers Aaron Hagerstrom and Thomas Murphy might be able to demonstrate the model in an optics experiment.

The Maryland group devised the experimental scheme shown in figure 1a. A polarizing beamsplitter filters linearly polarized light from an IR beam, and that light is then circularly polarized by a quarter-wave plate. A spatial light modulator (SLM), comprising a 512 × 512 array of liquid-crystal pixels, then reflects the beam and reshapes its wavefront. Each pixel i shifts the relative phase of the light’s horizontal and vertical polarization components by ϕ_i.

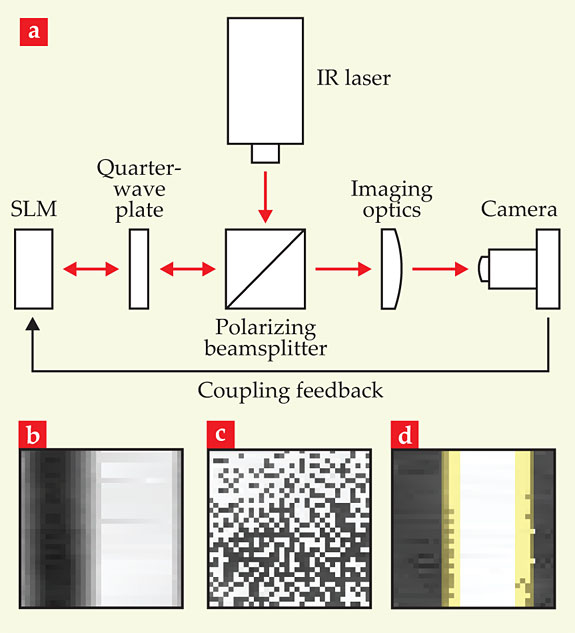
If ϕ = 0, reflected rays simply follow their original path in reverse: They are linearly polarized by the quarter-wave plate, filtered by the polarizing beamsplitter, and deflected back toward the laser source. If ϕ is nonzero, the reflected rays arrive at the beamsplitter with a polarization component that’s orthogonal to the filter angle. Thus some of the reflected light passes through, unfiltered, to a camera on the opposite side. The camera image that results comprises an array of pixels, with each pixel’s brightness related to the phase shift imposed by the corresponding pixel in the SLM.

To couple the pixels to one another, the researchers incorporated a computer-mediated feedback loop between the camera and the SLM. The effect of the feedback is to nudge the phase shift of each pixel toward the mean phase shift of its neighbors lying within a radius R; the precise magnitude of the nudge depends on the choice of coupling strength ϵ.

The camera images capture the subsequent evolution of the system’s dynamical state. For certain choices of R and ϵ, the apparatus yields a uniformly dark or bright screen, an indication that the pixels in the SLM share a coherent phase. Other combinations yield images of smoothly varying intensity, as shown in figure 1b. Still others produce randomly interspersed dark and bright pixels—evidence of spatial incoherence—as shown in figure 1c.

A small sliver of parameter space, however, gives rise to images like the one shown in figure 1d, in which uniformly dim and bright regions are separated by regions in which dim and bright pixels are interspersed. Those images indicate the emergence of a partially coherent, partially incoherent chimera state.

A chemical chimera

In the West Virginia experiment, Showalter and coworkers Mark Tinsley and Simbarashe Nkomo exploited an oscillating chemical reaction known as the Belousov–Zhabotinsky reaction (see Physics Today, April 2009, page 14 ). The researchers coated 40 microparticles with a ruthenium catalyst and immersed them in a cocktail of bromine compounds. In the reaction that ensues, the ruthenium catalyst is alternately oxidized and reduced, and each particle can be ascribed a phase that characterizes the reaction’s local progress. That phase can be monitored by charting the particle’s optical properties: When ruthenium is in its reduced state, the particles are nearly opaque; when the catalyst is oxidized, the particles become virtually transparent.

The researchers used a photosensitive version of the Belousov–Zhabotinsky reaction, which allowed them to manipulate—and couple—the particles’ phases by controlling each particle’s exposure to light. As shown in figure 2a, the team set up a camera to capture real-time images of the reacting particles. Based on each particle’s appearance, an algorithm calculates particle-specific optical feedback signals, which are then administered by an SLM projector.

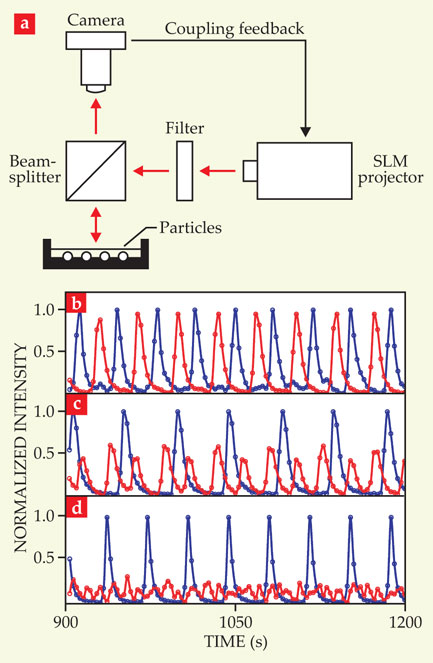
The feedback loop works to bring each particle in phase with the others according to a coupling strategy proposed by Strogatz and Abrams: The particles are split into two groups of equal size and, although every particle is coupled to every other particle, intragroup couplings are strongest.

In the experiment, one group of particles always synchronizes. But depending on the relative strengths of inter- and intragroup coupling, the second group may synchronize with the same frequency as the first, as shown in figure 2b; split into two synchronized subgroups—a so-called phase-cluster state—as shown in figure 2c; or re-main unsynchronized, as shown in figure 2d. The part-synchronous, part-asynchronous state is the chimera state.

New behavior

“The exciting thing about these experiments,” comments Abrams, “is that they aren’t simply confirmations of previous theoretical and numerical results. They show new, unexpected behaviors.” He cites the phase-cluster states, observed by the West Virginia team, which don’t appear in similar analytical and numerical models. Likewise, the two-dimensional systems studied by Roy and coworkers were previously unexplored terrain.

Erik Martens, a mathematician at the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany, is enthusiastic about the work, but he notes that “ideally, you’d like to be able to construct a chimera state that doesn’t rely on computational algorithms for the coupling. That might provide more insights into how chimera states might emerge in nature.”

Still, the experiments help to resolve at least one key question that has long surrounded chimera states: Can they survive amidst the noise of real-world environments? Abrams, for one, interprets the new findings as a convincing yes.