Entanglement gets scaled up in an optical frequency comb

The appeal of quantum computing is that by making use of quantum systems in highly entangled states, one can feasibly solve problems (such as factorizing large integers) that would take far too long on even the most powerful of classical computers. Still, useful quantum computation would require a register of some hundreds or thousands of quantum entities, such as two-level qubits or continuously valued qumodes. Scalability in the control over quantum information is thus an important research goal.

Toward that end, Olivier Pfister and colleagues at the University of Virginia have shown that in a single step, they can simultaneously manipulate at least 60 qumodes, entangling them in sets of four. ¹ Their experiment is a step toward implementation of a scheme called one-way quantum computing.

One way or the highway

The most familiar approach to quantum computing is much like classical computing: Start with a blank slate of unentangled qubits, manipulate them in a controlled way that depends on the problem to be solved, and make measurements to read out the answer at the end.

A one-way quantum computer, in contrast, starts with the qubits already in a particular highly entangled state called a cluster state. ² The computation is then performed by making a series of single-qubit measurements. The advantage is that the hardest part—constructing the entangled state—is all done in advance and is the same for every computation. The single-qubit measurements are comparatively easy.

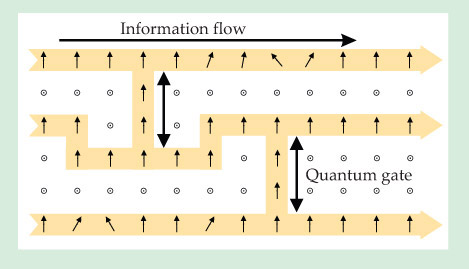
Basic elements of the scheme are illustrated in figure 1. The cluster state is a square lattice of qubits in which each nearest-neighbor pair is directly entangled. The qubits are measured sequentially, from left to right, in the directions shown by the black arrows. (The ⊙ symbols are arrows pointing out of the plane of the page.) A chain of in-plane measurements serves to either propagate the state of a qubit (vertical arrows) or rotate it (tilted arrows) along the chain. The conjunction of two chains forms a simple quantum gate, which can be combined to construct the quantum analogues of classical logic gates. The out-of-plane measurements serve to clean up the extraneous sites and keep the information chains separate.

One can also design a scheme for a one-way quantum computer based not on qubits but on continuously valued qumodes, such as squeezed optical modes. ³ A coherent light beam has an inherent quantum uncertainty in its electric field; in a squeezed optical state, the uncertainty in one part of the wave cycle is reduced at the expense of another. Two optical beams are entangled if their correlations—uncertainty in their sum or difference, for example—display the characteristics of a squeezed state.

To create entangled states of light, researchers typically use an optical parametric oscillator (OPO), a combination of an optical cavity and nonlinear crystals that split input photons into pairs of lower-energy output photons, subject to conservation of energy and momentum. The quantum fluctuations of the input, or pump, mode are transferred onto both of the output modes, which are thereby entangled.

Most efforts to entangle optical modes into a cluster state suitable for quantum computing involve building up the state bit by bit. Making a larger cluster state thus requires more hardware and effort. But, as Pfister and theorists Steven Flammia and Nicolas Menicucci determined, the equipment and effort might be greatly reduced by using an optical frequency comb—the equally spaced modes of an optical cavity—as the qumodes. ⁴ A suitably designed OPO could entangle many pairs of modes with a single pump mode, because there are many pairs of modes whose frequencies sum to the pump frequency. The researchers developed a scheme whereby a single OPO and a pump spectrum of 15 frequencies suffice to create the topological equivalent of an arbitrarily large cluster state. Pfister and his experimentalist colleagues have now taken the first step toward implementing the scheme in the lab.

Entangling qumodes

Flammia, Menicucci, and Pfister found that to create a cluster state with the desired topology it is necessary to use the y and z polarizations of a single frequency as separate qumodes. To address both polarizations, and to create entangling interactions between modes of different polarization, the OPO must be highly exotic, consisting of two distinct nonlinear crystals, one rotated with respect to the other.

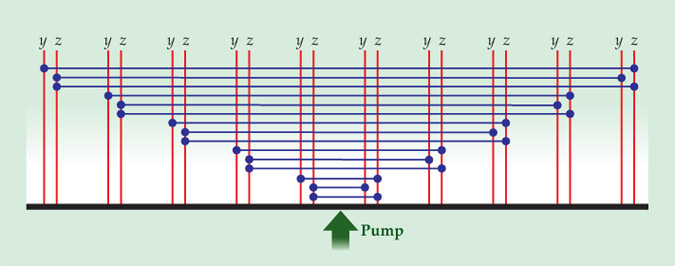
Getting the alignment of the crystals just right, and controlling the relative strengths of their nonlinear processes, was an experimental challenge, but Pfister and colleagues have now achieved their first success by entangling modes in groups of four. As shown in figure 2, that could be accomplished with a single pump frequency, since each cluster of four entangled modes comprises just two frequencies.

To test the entanglement, the researchers measured the noise level in the electric field as a function of phase for linear combinations of the entangled modes. To make the phase-specific measurements, they combined the frequency comb modes with a two-color local oscillator, a beam whose spectrum contained the two frequencies whose entanglement they wanted to check. They ran the check on 15 clusters of modes that they expected to have entangled, starting with the adjacent modes in the frequency comb, as shown in the left panel of figure 3, and ending with the widely spaced pair shown in the center panel. A noise level of 0 dB is the minimum level of quantum fluctuations of modes that are unsqueezed and unentangled; noise levels below 0 dB constitute entanglement.

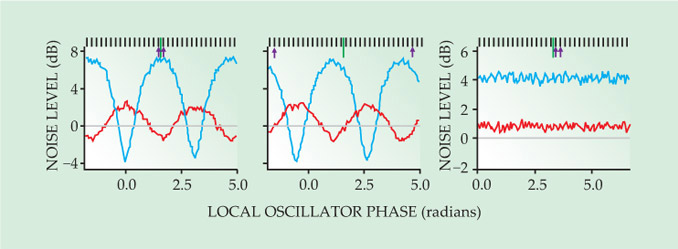
All the clusters the researchers checked were entangled, and to an almost identical degree. They could check only 15 clusters because of technical limitations in the local-oscillator frequencies they could produce; it’s likely that they actually entangled at least 45 four-mode clusters, and possibly as many as 150.

Equally important to the eventual formation of a large cluster state is to ensure that there is no entanglement between modes that shouldn’t be entangled. And indeed, that is what the researchers found, as shown in the rightmost panel of figure 3.

Connecting the four-qumode clusters into larger cluster states is mostly just a matter of adding more frequencies to the pump spectrum. But before the optical cluster state can be used for quantum computation, an additional challenge must be overcome. Simple electric-field measurements, as with the local oscillator, don’t work as the single-qumode measurements in a one-way quantum computing scheme. Instead, it’s necessary to count the mode’s photons with 100% efficiency. “Such measurements were unthinkable just a few years ago,” Pfister says, “but Sae Woo Nam’s group at NIST has made giant strides in that respect, and photon-number-resolving detection has now come of age.”