Custom shapes from swell gels
DOI: 10.1063/PT.3.1543
The curves and folds of a flower, the wrinkling of our skin, and the wavy edge of torn plastic are among the countless examples of patterns that emerge from the physics of thin elastic sheets. As cells grow nonuniformly in a petal, say, or as ripped plastic deforms along its edge, stresses build up. To accommodate the deformation and relieve the stress, the material has to either compress internally or bend. Both distortions cost energy, but which one Nature chooses depends directly on thickness: The thinner the sheet, the cheaper it is to buckle out of the plane.
For the past decade, researchers have been striving to translate that competition between compression and bending into practical strategies for controlling the shape of a thin film embedded in our three-dimensional world. The mechanism by which in-plane stresses actually break a sheet’s local symmetry is subtle, mathematically formidable, and not entirely understood. But fortunately, one can turn to differential geometry, which has long been deeply entwined with the theory of elasticity, to engineer structures (see the article by Michael Marder, Robert Deegan, and Eran Sharon in PHYSICS TODAY, February 2007, page 33
In 2007 Eran Sharon realized the theorem could be used as a shape-selecting principle, provided one could inscribe the required lateral stresses on a flat sheet to generate a new target metric. In response to those stresses, the sheet would ideally settle into an equilibrium configuration that, properly buckled, minimizes the elastic energy and realizes the new metric. As proof of principle, he and colleagues from the Hebrew University of Jerusalem demonstrated the idea, at least for axially symmetric shapes, using disks of temperature-sensitive polymer gels. 1
Now, University of Massachusetts Amherst researchers led by polymer scientist Ryan Hayward and physicist Christian Santangelo have generalized the idea into a lithographic method that can produce, at least in principle, a nearly arbitrary 3D shape. 2 What’s more, it’s inexpensive, easily reproducible, and potentially scalable—from areas under a square millimeter, as tested in the first implementations, to, says Hayward, areas of several square centimeters.
Designed response
The method starts with a thin (typically 10-μm) film of hydrogel, a cross-linked network of polymer chains. When cooled in a water bath to about 22 °C, the gel swells by absorbing water until the osmotic pressure balances the pressure exerted by the polymer chains. The extent of the swelling depends on the strength of the cross-linking, which, in turn, depends on the gel’s prior exposure to UV light. One can thus tune the shape shifting: The gel’s lightly exposed areas have weaker linking and can swell nearly four times as much as its heavily exposed ones—and do so in a few minutes’ time.
To pattern a polymer film with the exposures required for it to spontaneously adopt a shape consistent with a target metric, the Amherst team used a photomask made of an evenly spaced array of holes with varying diameters—a process akin to half-tone printing in a newspaper. Provided the polymer sheet wasn’t too thin, its elasticity turned out to be sufficient to locally smooth out the sharp contrast between highly cross-linked dots and the lightly cross-linked matrix.
The researchers tested the method by creating shapes, as shown in figure 1, that correspond to several axisymmetric metrics: a saddle, a cap, a dome, and a so-called Enneper minimal surface. Conveniently, they were able to adapt well-established formulas for the metrics from differential geometry; in each case they calculated the pattern of dots needed to produce the appropriate swelling factor Ω at each point on the lattice.

Figure 1. Originally flat sheets of polymer gel adopt a Gaussian curvature that is either positive (as with the dome and cap in the middle) or negative (as with the saddle and ruffled edges of the Enneper surface on the ends), depending on how they are patterned with UV light. The larger the red dots, the greater the UV exposure and the smaller the swelling. (Adapted from ref.

Producing the sphere shown in figure 2a turned out to be trickier. A number of conformal mappings of a sphere onto flat surfaces are known from the field of map projections. But to go beyond a hemisphere, the Amherst researchers had to use a nonaxisymmetric metric that would accommodate the gel’s limited ability to swell: Charles Sanders Peirce’s 1879 quincuncial projection. Even with it, they had to excise parts of the square where Ω falls below the experimentally accessible range.
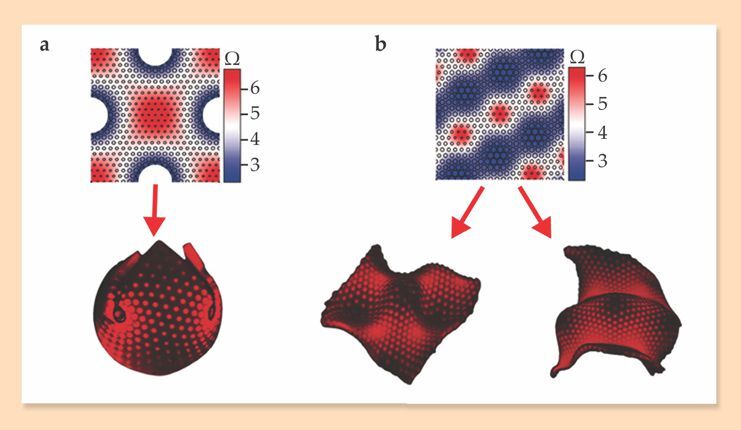
Figure 2. (a) This swelling pattern (top) illustrates the sizes of the mask holes required for a roughly 600-µm square sheet to warp into a spherical shell (bottom). The colors illustrate the range of the gel’s local swelling factor Ω. (b) A pattern designed to produce an egg carton (left) may inadvertently produce an entirely different shape (right) instead. The three local maxima in growth, lying along the diagonal, each represent a region of positive Gaussian curvature—either a peak or trough. But the buckling configurations, up or down, are nearly degenerate in energy. So even slight variations in parameters such as local thickness can lead to very different shapes. (Adapted from ref.
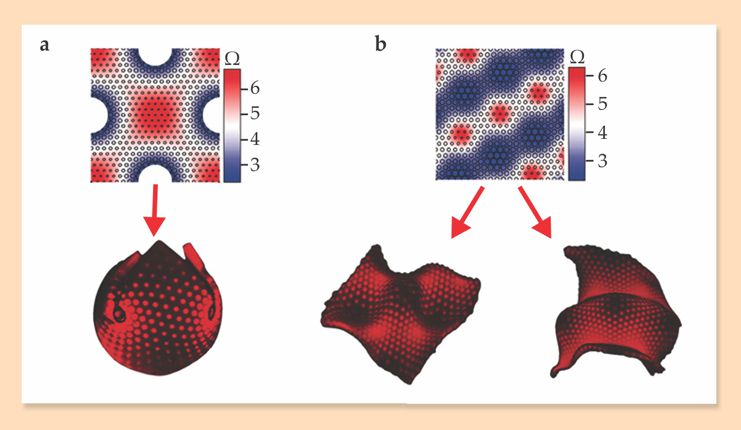
Nonetheless, the new method opens the door to shapes of arbitrary complexity. Initial efforts suggest that it’s sometimes not enough to find the swelling function that defines a particular metric. For instance, when the group patterned the gel into a corrugated surface, the sheets often failed to adopt the intended egg-carton shape, as suggested in figure 2b. Because of slight variations in film thickness, for example, or the existence of multiple shapes that are locally metastable, sheets can misfold. Indeed, very different shapes may emerge from nearly identical metrics.
The opposite is also true. Two shapes that look nearly identical may come from very different metrics, a fact that may bear on the best way to design certain kinds of objects. Applications in soft robotics, tunable optics, biomedicine, and elsewhere may come eventually. But for now, says Santangelo, “This is a toolkit for doing math with experiments.”
References
1. Y. Klein, E. Efrati, E. Sharon, Science 315, 1116 (2007). https://doi.org/10.1126/science.1135994
2. J. Kim et al., Science 335, 1201 (2012). https://doi.org/10.1126/science.1215309




