Circular polarization is made to order in the extreme UV

Birefringent materials, characterized by their direction-dependent indices of refraction, are powerful tools for manipulating light’s polarization. Held one way, a birefringent crystal serves as a polarization analyzer that separates a light beam into orthogonally polarized components—or puts those components back together again. Held another way, the crystal becomes a wave plate that retards one polarization component with respect to the other. As figure 1 shows, the sum of two suitably phased linearly polarized waves is circularly polarized. So with the right arrangement of birefringent components, one can engineer light with linear or circular polarization or any of the continuum of elliptical polarization states in between.

Figure 1.

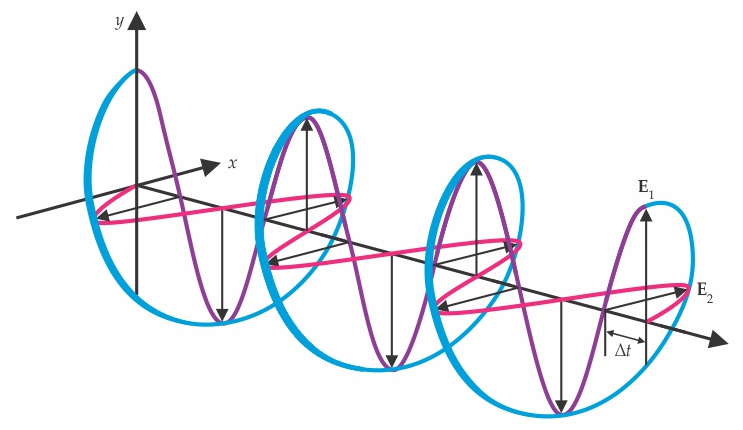
Circularly polarized light is important because of its capacity to distinguish between the mirror-image forms of molecules that are asymmetric, or chiral—a category that includes almost all biomolecules and many of the substances that interact with them (see Physics Today, July 2018, page 14 ). Chiral materials absorb right- and left-circularly polarized light in different amounts. By measuring that differential absorption, or circular dichroism, one can infer, among other things, which chiral form is present and in what quantity.

Now Nirit Dudovich of the Weizmann Institute of Science in Israel, her graduate student Doron Azoury, and their colleagues have demonstrated a new scheme for achieving full polarization control in the extreme UV (XUV), ¹ the electromagnetic regime with photon energies between 10 eV and about 100 eV. Circular polarization in the XUV, and in the next higher frequency band of soft x rays (photon energies up to 1 keV), can be used to study the magnetic structure of materials. But until recently, the requisite polarization control has been available only at large synchrotron facilities (see the article by Neville Smith, Physics Today, January 2001, page 29 ). Dudovich and colleagues’ tabletop scheme produces XUV pulses that are attoseconds in duration, so they have the potential to probe not only the structures of chiral materials but also their ultrafast dynamics (see Physics Today, January 2018, page 18 , and June 2018, page 20 ).

Not so impossible

Researchers who work in the attosecond regime generate their ultrashort XUV pulses using a process called recollision. (See the article by Henry Kapteyn, Margaret Murnane, and Ivan Christov, Physics Today, March 2005, page 39 .) An intense, linearly polarized IR pulse, with a photon energy of 1.6 eV or less, is focused on a target gas. As the electric field reaches peak value, it pulls electrons away from their parent atoms; the electrons then slam back into the atoms and produce a short burst of linearly polarized XUV photons. Each swing of the IR electric field produces a new burst; converted to frequency space, the train of XUV pulses corresponds to a ladder of high harmonics of the IR frequency.

But using a circularly polarized IR input doesn’t yield circularly polarized harmonics, or indeed any XUV emission at all: The electrons and parent atoms are driven apart and never recollide. It’s possible, it turns out, to produce circularly polarized high harmonics in the XUV and soft-x-ray regimes by superposing circularly polarized IR and visible light so that the net electric field oscillates in a trefoil pattern. ² But the polarization depends on the harmonic number, and the strong-field nature of the interaction makes the output polarization difficult to fully tune.

Dudovich and her colleagues use a different approach to polarization control that’s similar to the conventional birefringent-crystal scheme. With different portions of a single IR starting wave, they generate two copropagating linearly polarized XUV pulse trains. By independently controlling the electric field vectors E₁ and E₂ and the time delay Δt between the two waves, they can straightforwardly dial up any XUV polarization state.

The experimental setup is depicted in figure 2. An IR pulse, focused in the first of two XUV source gases, generates an XUV pulse train with electric field vector E₁. But not all of the incoming light has its frequency upconverted; much of it, especially around the edges of the beam where the intensity is lower, passes through the first source unchanged. That remaining IR radiation, focused into another XUV source, generates a second pulse train with electric field vector E₂.

Figure 2.

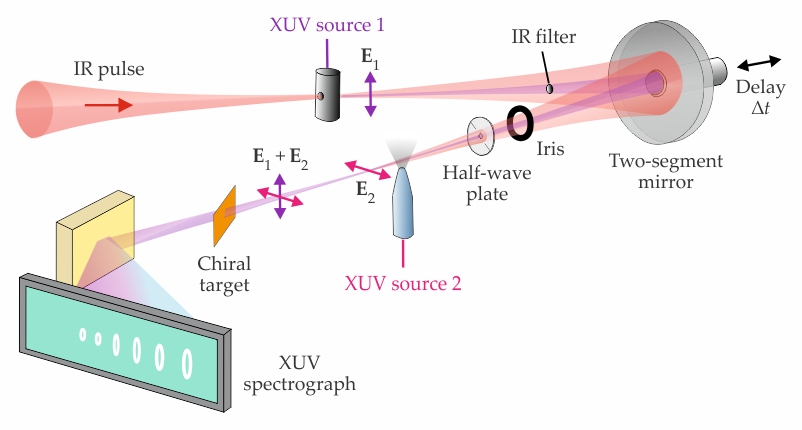
The optics components between the two XUV sources enable the researchers to control the properties of the two pulse trains. First, a filter blocks any residual IR from the center of the beam and allows the XUV pulse train in the middle to be manipulated separately from the IR in the outer annulus. A concentric two-segment mirror introduces a time delay Δt between the two components. An iris provides a way to control the magnitude of E₂ by trimming away the edges of the IR beam. And a half-wave plate, with a hole drilled in the middle to let the XUV pulses pass through, rotates the polarization of the IR beam and thus controls the direction of E₂.

Because XUV wavelengths are so short, getting the two XUV pulse trains to combine coherently into the desired elliptical polarization requires the whole setup to be extraordinarily stable. “Even with the core idea in hand, it isn’t at all obvious that the experiment is actually feasible,” says Emilio Pisanty of the Institute of Photonic Sciences in Barcelona, Spain. “If anyone had suggested this idea 10 years ago, they would have been laughed out of court for suggesting the impossible.”

Dudovich and colleagues got their first inkling that it might be possible two years ago, when during a routine calibration of an unrelated experiment they observed a hint of interference between XUV waves with a photon energy of 15 eV. “Motivated by our accidental discovery, we introduced substantial stability upgrades,” explains Azoury, “and finally were able to demonstrate interferometric optical control up to a photon energy of 60 eV.” Higher energies than that—the range of greatest interest for magnetism studies—will require greater stabilization than Dudovich’s group has so far achieved.

Locked in

The simplest approach to measuring circular dichroism entails separately quantifying the absorption of right- and left-circularly polarized light and then subtracting. It doesn’t always work in practice. Chiral effects in real-life samples are often small, and small differences between large measured quantities are prone to large uncertainties. A more sensitive detection method is to modulate the incident light’s polarization and look for a signal oscillation at the same frequency. Dudovich and colleagues’ new scheme makes that approach possible in the XUV: Modulating the polarization is as simple as scanning Δt by moving the center mirror a short distance at a controlled speed.

The advantages don’t end there. The scheme offers control over a degree of freedom that’s less easily accessible with real birefringent crystals: the angle between E₁ and E₂. In the setup shown in figure 2, the half-wave plate is positioned with its axis at a 45° angle to E₁; the IR polarization is thus rotated by twice that angle, or 90°, and E₁ and E₂ are orthogonal. By reorienting the half-wave plate, one can set the angle θ between the polarization vectors to any desired value.

That flexibility facilitates the lock-in detection of chiral signals. Figure 3 illustrates how it works. In panel 3a, E₁ and E₂ are parallel. Their sum always has the same linear polarization but varies in intensity with Δt as the components constructively and destructively interfere. The transmission through a chiral target is proportional to the incident intensity but gives no information about the target’s chiral structure.

Figure 3.

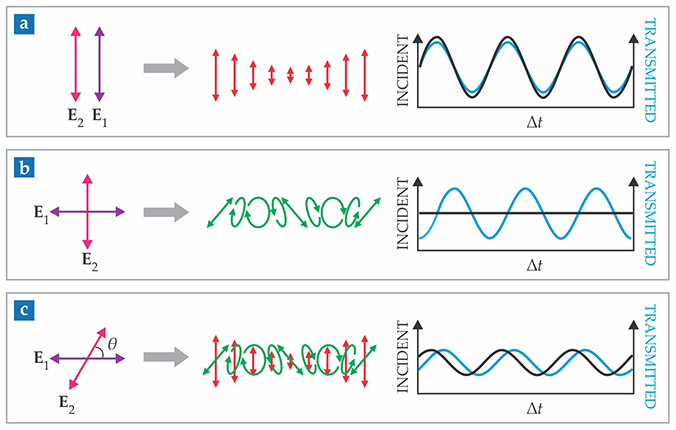
Panel 3b shows the case of θ = 90°. Scanning Δt leaves the intensity of the combined wave unchanged but modulates its polarization. Transmission through a chiral target also oscillates, and the magnitude of the chiral effect can be inferred from the oscillation amplitude. Panel 3c, which shows an intermediate θ, is effectively a superposition of panels 3a and 3b. Both the incident and transmitted intensities oscillate with Δt, and the chiral signal is encoded in the phase shift between them. Phases are less sensitive than amplitudes to intensity fluctuations in the incident wave, so they can be more accurately measured.

Because the scheme works in the time domain, it’s possible, at least in principle, to isolate a single circularly polarized attosecond pulse, whose frequencies span a broad XUV continuum. In contrast, the previous approach using a trefoil-evolving electric field is inherently limited to a series of discrete harmonics: Each pulse in isolation is linearly polarized, and only when a long train of pulses are taken together are the harmonics circularly polarized. Chiral effects in many materials manifest in spectral features as narrow as a fraction of an eV, so full spectral coverage is important. ³

“Most experiments to date have been looking at toy systems where the features are extremely broad and the exact wavelength is irrelevant,” says Allan Johnson of the Institute of Photonic Sciences. “This is probably the first time I’ve felt that circularly polarized harmonics could seriously make it out of attosecond labs and be taken up as a general tool.”