Charged polymers form unusual nanostructures

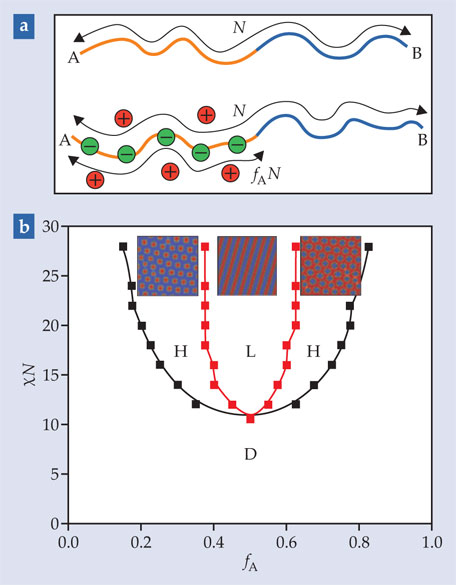
Diblock copolymers—made up of a chain of monomer A bound to a chain of monomer B, as shown in figure 1a—are of great theoretical and practical interest. When the A and B monomers are sufficiently immiscible, they can segregate into self-assembled periodic nanostructures such as alternating layers or hexagonally ordered rods. The morphology of those two-phase structures depends on the phase immiscibility, the relative lengths of the A and B chains, and other factors. Choosing the A and B phases with complementary properties enables a variety of applications. (See the article by Frank Bates and Glenn Fredrickson, Physics Today, February 1999, page 32 .)

For example, to make a solid-state electrolyte for a battery or fuel cell, one can optimize the A phase for ionic conductivity, with negative ions bound to the polymer chains balanced by unbound positive ions, and the B phase for mechanical stability. Numerous experiments, however, have shown that the theoretically derived phase diagram that predicts the nanophase morphology no longer applies when one of the phases is charged. ¹

Monica Olvera de la Cruz and colleagues at Northwestern University have developed a new theory that accurately describes the ion-rich A phase by accounting for correlations among the charged monomers and ions. ² Tuning the strength of those correlations, which depends, most importantly, on the dielectric constant of the A phase, can induce qualitative changes in the A phase’s morphology.

Ionic effects

The canonical phase diagram for neutral diblock copolymers, shown in figure 1b, illustrates how, as a function of the fraction f_A of A monomers and phase immiscibility χ, the polymers can be disordered or can form layered or hexagonal structures. The phase boundaries are derived from self-consistent field theory (SCFT), which is founded on the assumption that as the polymers move around, each one responds to the mean density of all the others—so instead of solving the many-body problem of all the polymers simultaneously, one need only look at the problem of a single polymer moving in an applied field. For neutral-polymer systems, that assumption seems to be good: SCFT has been successfully used for decades to describe various aspects of phase segregation in neutral polymers and copolymers.

Applying SCFT to a charged polymer system means assuming that each charge—whether free or bound to a polymer—feels the average electric field of all the other charges. Such a treatment results in a phase diagram of the same shape as the one in figure 1b, but shifted down by an amount proportional to the fraction of charged monomers in the A phase. ³ That is, the immiscibility χ is replaced by an effective immiscibility, and everything else is the same.

In general, though, ions in polymeric materials don’t behave like the structureless sea of charge that SCFT assumes. When the A phase’s ion concentration is low or its dielectric constant is high, charges are screened from each other, so they act almost independently, and SCFT is almost right. But as the charge fraction increases or the dielectric constant decreases, charges form correlated clusters, which exert local forces on the material and have the potential to influence its structure.

A useful theoretical treatment of charged diblock copolymers, then, requires that ion–ion interactions be treated explicitly without making the polymer calculations computationally intractable. Olvera de la Cruz and colleagues’ solution was to continue to describe the polymers with SCFT and to treat the ion clusters with so-called liquid-state theory, which has long been used to study fluids of strongly coupled ions. Postdoc Charles Sing, an expert in SCFT, worked with senior scientist Jos Zwanikken, an expert in liquid-state theory, to unite the two theories in a single computer code.

The result was a phase diagram that depends on four parameters: f_A and χ from the neutral polymer case; the ion concentration in the A phase; and Γ, a measure of the strength of charge correlations, inversely proportional to the A phase’s dielectric constant. Cross sections of that four-dimensional parameter space for particular values of the charge fraction and Γ can yield two-dimensional phase diagrams that are severely distorted from the neutral case.

Figure 2 shows one example. In a neutral system, the “inverse-hexagonal” phase, consisting of rods of monomer B in a sea of monomer A, occurs only when f_A > 0.5—that is, when the A block is longer than the B block. But at high enough values of the charge fraction and Γ, that phase is shifted to much lower values of f_A. Inverse-hexagonal phases in systems with low f_A have been experimentally observed before. ⁴ But until now, there’s been no complete map of the 4D parameter space to show under what conditions they might occur.

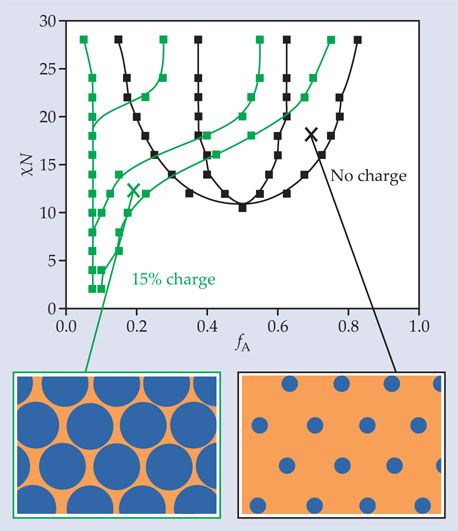
The ability to create inverse-hexagonal phases is potentially important for designing solid-state electrolytes because a continuously connected A phase allows ion transport in any direction. Even for applications in which conductivity isn’t important, access to different structures may prove useful, and tuning the charge fraction to change the morphology may be easier than tuning χ. “Beyond reproducing the curiosities of the existing literature,” says Olvera de la Cruz, “our theory allows block copolymer systems to be manipulated in a way that’s been explored in only a precursory manner. It’s now up to the experimenters to explore that manipulation for both batteries and other materials.”