Casimir forces between solids can be repulsive

The Casimir force, a result of zero-point electromagnetic fluctuations, is a quantum mechanical effect that can influence the mesoscopic and macroscopic worlds. It acts between any two objects, but it’s so weak that it has typically been considered little more than a theoretical curiosity. Usually, the interaction is attractive. But now, Harvard University’s Federico Capasso and his recently graduated student Jeremy Munday have observed a repulsive Casimir force—even weaker than the attractive version and with possible applications to nanoscale technology. ¹

The Casimir force is a close cousin of the van der Waals force between non-polar molecules or larger objects. When the ever-moving charges in one object create a momentary electric dipole, they can induce a dipole in a nearby object such that the two dipoles attract each other. In the van der Waals limit, the objects are close enough that the electric field propagates between them much faster than the charges can oscillate in either object. But in the Casimir regime, the objects are farther apart, the finite speed of light becomes important, and the dependence of the force on the objects’ separation is suitably modified.

Another way to look at the interaction is in terms of the zero-point energy of electromagnetic waves. In infinite free space, waves can have any frequency, but between two conducting plates, they’re limited to the frequencies that allow an integral number of half wavelengths to fit in the gap between the surfaces. The vacuum energy therefore depends on the plates’ positions, so the plates experience a force that turns out to be attractive.

Hendrik Casimir’s 1940s calculations (described by Steve Lamoreaux in Physics Today, February 2007, page 40 ) assumed that the plates were perfect conductors. ² Later on, Evgeny Lifshitz and colleagues generalized Casimir’s work to real materials—nonperfect conductors and dielectrics—and considered the case in which the plates were separated by a fluid, not a vacuum. ³ They found that repulsive forces should result from materials with a certain relationship among their frequency-dependent dielectric permittivities. When plates of a high-permittivity material and a low-permittivity material are separated by a fluid of intermediate permittivity, a larger momentary polarization is induced in the fluid than in the low-permittivity plate. The fluid is drawn to the high-permittivity plate more strongly than the two plates are drawn to each other, so there’s a net repulsion between the plates. Notes Capasso, “That’s not a rigorous explanation, but it’s one way to understand the phenomenon.”

Finding repulsion

Repulsive cases of the Casimir–Lifshitz force, as it’s now often called, are not uncommon. They can be found whenever a liquid completely wets a solid surface: The solid and the air or ambient vapor effectively repel each other, and the liquid spreads out to fill the gap. In a similar but more spectacular example, Casimir–Lifshitz repulsion is also responsible for liquid helium’s tendency to climb the walls of its container.

Combinations of materials that produce repulsive Casimir–Lifshitz forces between solid objects are harder to come by, but they’re not unknown. ⁴ Indeed, some have been tested already, such as gold and Teflon separated by cyclohexane, and repulsive forces have been observed. ⁵ But those forces were detected only at separations of a few nanometers or less: within the van der Waals limit, which in the gold-cyclohexane-Teflon case is determined by the plasma frequency of gold. And at such small length scales, the force can be complicated by surface roughness and the intervening liquid’s inhomogeneity—the arrangement and orientation of its individual molecules.

Capasso and Munday chose gold and silica as their solid materials. With the help of Adrian Parsegian (of the National Institutes of Health in Bethesda, Maryland), an expert on the chemical physics of van der Waals forces, they eliminated or accounted for many subtle effects that could interfere with their force measurement—and that might have been what prevented previous researchers from observing repulsive forces at a longer range. For example, any static charge trapped on the silica surface would induce an image charge in the gold and thereby produce an attraction. So Capasso and Munday checked that their ultrasonic cleaning procedure left no measurable surface charge on the silica.

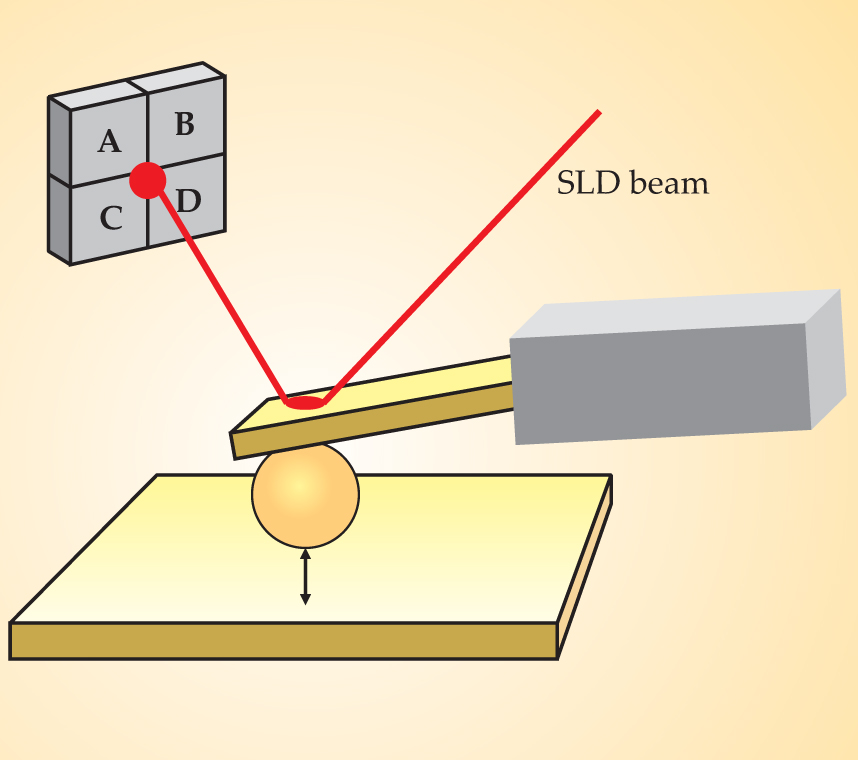
Using a standard method for measuring Casimir forces, as shown in figure 1, the researchers attached a 40-µm gold-coated sphere to an atomic force microscope cantilever. They then lowered the sphere over a surface of gold (for comparison) or silica and monitored any additional deflection of the cantilever using a split-quadrant photodetector and a light beam from a super-luminescent diode. (The sphere–plane configuration is a bit more complicated to analyze theoretically than Casimir’s original plane–plane conception, but it makes the experiment much easier, because keeping the planes exactly parallel is not a concern.) They first tried the experiment in ethanol, but ultimately changed to bromobenzene, a less polar substance that also satisfies the necessary permittivity relationship over a wide range of frequencies.

The results are shown in figure 2. As expected, for the gold–gold configuration in figure 2(a), the interaction was attractive: As the cantilever was lowered, the sphere was pulled toward the surface until it made contact, as indicated by the abrupt change in slope of the deflection curve. When the cantilever was retracted, the sphere stuck to the surface as the cantilever was raised an additional 10 nm—the attraction is stronger when the sphere and the surface are already in contact than when they’re not—and then was pulled loose.

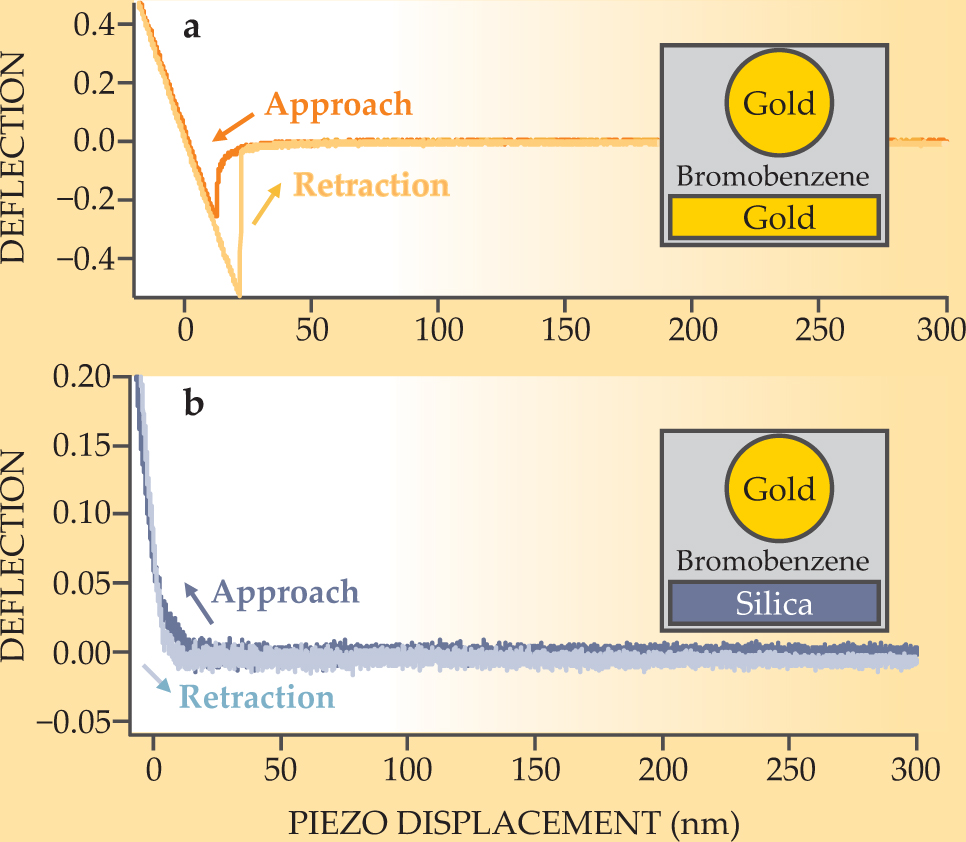
For the gold–silica combination in figure 2(b), the cantilever was deflected upward during both the approach and the retraction. To convert the cantilever deflection data into a force measurement, the researchers had to isolate the effect of the Casimir–Lifshitz force from that of the hydrodynamic force of the bromobenzene on the gold sphere. Because that drag force is proportional to the velocity of the sphere, its contribution could be determined by repeating the experiment at different speeds. With the drag force thus canceled out, Capasso and Munday were able to measure repulsive forces of tens of piconewtons for sphere–surface separations of up to 40 nm.

Levitation applications

From the beginning, Capasso’s interest in the Casimir–Lifshitz force was in part motivated by its relevance to microelectromechanical systems, or MEMS. If two parts of one of those tiny devices get too close to each other, they stick together and render the system inoperable. The phenomenon is called stiction, and it’s thought that the Casimir–Lifshitz force is responsible. Reducing or eliminating the attractive Casimir–Lifshitz force among MEMS components could alleviate the problem of stiction as MEMS are further miniaturized. And actually reversing the force into a repulsion allows the intriguing possibility of levitating one object above another. If a levitation gap can be achieved that’s larger than any surface roughness features (typically around 15 nm), it could allow the creation of very low-friction force sensors, bearings, or other devices.

Capasso also hopes that Casimir levitation will help him observe a quantum electrodynamical torque between optically anisotropic materials. By levitating one disk of birefringent material above another, he says, it should be possible to rotate the top disk with circularly polarized light and see that the disks’ principal optical axes tend to align when the light is removed. ⁴