An optical trap nudges a nanoparticle into its motional ground state

Macroscopic objects tend to behave classically rather than quantum mechanically—unless they can be cooled to ultralow temperatures. With a macroscopic quantum system, physicists could elucidate both the transition from classical to quantum and the causes of decoherence, including the role of gravity. Such systems would also have potential sensor applications for small forces (see Physics Today, October 2018, page 19 ).

A suite of laser-cooling techniques has successfully pushed the temperature of atomic gases down to within a fraction of a degree above absolute zero, where quantum mechanics dictates their behavior. But the gases are not in macroscopic superposition states. Another potential route to macroscopic quantum systems is quantum optomechanics, in which an optical cavity is paired with a mechanical resonator of dimensions up to hundreds of millimeters (see the article by Markus Aspelmeyer, Pierre Meystre, and Keith Schwab, Physics Today, July 2012, page 29 ). Although researchers have cooled those systems to their ground state mechanical modes, the research applications are limited because the resonator is attached to a support and can’t be manipulated as a single, isolated object.

Now Markus Aspelmeyer of the University of Vienna in Austria and his colleagues have demonstrated a strategy for an easily manipulated macroscopic quantum system. ¹ They cooled a nanoparticle to its ground state, as depicted in figure 1, through a cooling technique that pairs an optical trap with an optical cavity.

Figure 1.

From atoms to nanoparticles

Extending laser-cooling techniques to molecules and solids has proven tricky. The most common technique, Doppler cooling, irradiates the sample from all sides with laser light that is tuned slightly below the frequency of an atomic transition. When an atom moves in the opposite direction of a photon, the light is blueshifted into resonance and absorbed. The atom then slows down, reemits the light, and returns to its ground state.

Repeating that absorption and emission tens of thousands of times can cool a sample to temperatures as low as tens of microkelvins. But a molecule’s rotational and vibrational degrees of freedom split the energy levels. Therefore, when a molecule reemits light, it can get stuck in a state other than the ground state and actually gain energy in the process (see Physics Today, January 2010, page 9 ).

About 20 years ago, Helmut Ritsch and, independently, Vladan Vuletić and Steven Chu proposed a different method called cavity cooling. ² It relies on coherent scattering in an optical cavity irradiated by a laser, which doesn’t need to be tuned to an electronic transition. The cavity field traps the atom or molecule, and when the light in the cavity scatters off it, the particle is left in either a higher motional energy state, so-called Stokes scattering, or a lower motional energy state, anti-Stokes scattering. The driving laser is tuned such that the cavity enhances anti-Stokes scattering, and each photon scattered into the cavity lowers the energy of the particle one quantum of motion, or phonon, at a time.

In theory, that tactic should cool a nanoparticle to its motional ground state. As Uroš Delić finished his undergraduate thesis in preparation for grad school, he and Aspelmeyer were eager to try cavity cooling on a solid particle, an effort pursued by a few groups, including that of Lucas Novotny at ETH Zürich. But any effort to reduce the temperature below tens of millikelvin, or several hundred phonons, faces two hurdles. First, fluctuations in the laser’s phase cause cavity-field fluctuations that jostle the particle and heat it. Second, cooling the nanoparticle further than tens of millikelvin requires more photons—that is, the laser intensity needs to be increased. But a strong cavity field pulls the particle into one of the field’s antinodes, where the particle motion no longer interacts with the cavity field and thus isn’t cooled.

After an internship in Vuletić’s lab at MIT, Delić altered the cavity-cooling setup in Aspelmeyer’s lab to remove those obstacles. In their cooling scheme, shown in figure 2a, he and Aspelmeyer incorporated an optical trap that they detuned by Ω from the cavity’s resonant frequency ω_cav . The trap (green) holds the particle in a stable position in the cavity and provides photons for the cooling process; no driving laser, with its phase noise, is necessary. Because the photons come from the trap, the particle can be cooled at any position in the cavity. Positioning the trap in a cavity field node removes elastic scattering (dashed green arrows) to leave only Stokes and anti-Stokes scattering.

Figure 2.

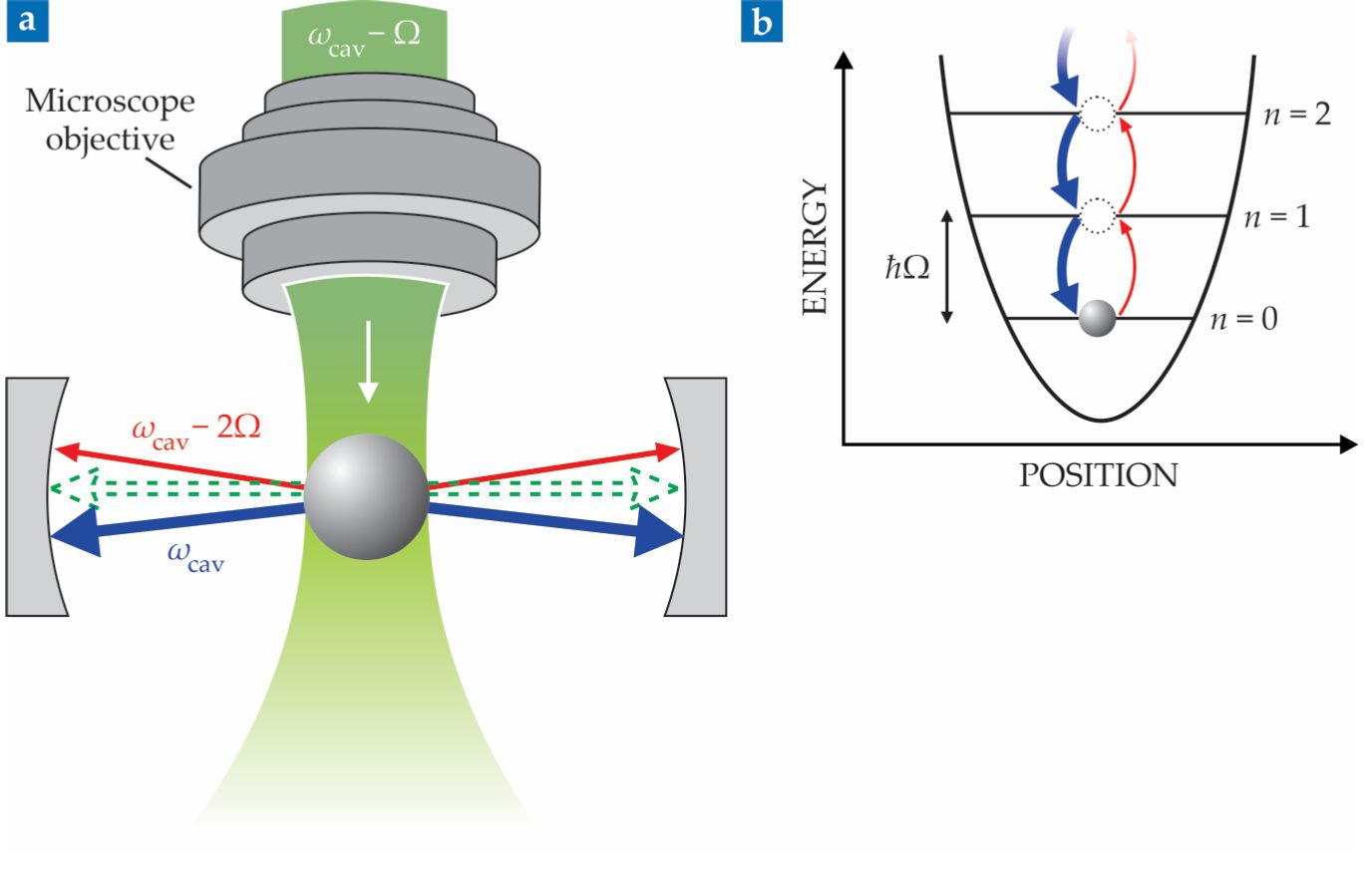
Otherwise, the process is similar to the usual cavity cooling: Photons from the trap scatter off the particle, and rather than enhancing Stokes scattering (smaller red arrows), the cavity enhances anti-Stokes scattering (blue arrows in figure 2b), which gradually lowers the particle’s energy. Aspelmeyer’s and Novotny’s teams both implemented cooling with an optical trap, ³ and they found it is much more efficient: It takes four to five orders of magnitude fewer photons than cavity cooling to reach the same temperature.

Fine tuning

The nanoparticle’s temperature is the sum of the phonons’ energies. To measure the number of phonons, Aspelmeyer and his team collect the scattered light and identify the frequency peaks from Stokes and anti-Stokes scattering. The evolving asymmetry of those peaks indicates the average number of phonons $\bar{n}$. The cavity enhancement leads to a much larger anti-Stokes peak when there are many phonons. But a particle in its ground state can’t reduce its energy further—that is, anti-Stokes scattering is no longer possible. As the temperature approaches that of the ground state, the anti-Stokes peak therefore shrinks, whereas the Stokes peak stays relatively constant.

In the experiment, the team members cooled a 143-nm-diameter silica nanoparticle down to its ground state, which corresponds to a temperature of about 12 µK. The lowest value of $\bar{n}$ they measured was 0.43; any value below 1.0 indicates the ground state. Previous cavity cooling studies reported nanoparticles with hundreds of phonons, and Novotny and his team reached four phonons using an optical tweezer with an active feedback loop. ⁴

To optimize the cooling, Aspelmeyer’s group members detuned the optical trap by different frequencies relative to the cavity resonance, as shown in figure 3. They found that detuning by about 315 kHz produced the minimum average number of phonons. But detuning by 380 kHz also dropped the particle to the ground state.

Figure 3.

Room for expansion

Now that Aspelmeyer has cooled a nanoparticle to its ground state, he says, “What I would really love to see is a wavepacket that is the size of the object.” In the current experiment, the nanoparticle’s wavepacket is localized to a few picometers. But a wavepacket as big as the particle itself would allow researchers to examine its properties in the macroscopic quantum regime.

Expansion of the wavepacket is possible by swapping the trap’s beam profile from a harmonic potential to a double well or any number of nonlinear potentials. Engineering particle dynamics quickly and on the fly through the beam profile is something the cold-atom and biophysics community has been doing successfully for years with optical tweezers. The particle stays trapped, and the potential landscapes evolve around it.

Another method to expand the wavepacket is turning off the optical trap and letting the particle fall. With the current setup, a freely falling wavepacket would have time to expand by only a factor of three before it decohered. Lowering the pressure to 10⁻¹¹ mbar and the surrounding temperature below 130 K would preserve coherence for long enough, about 10 ms, for the wavepacket to expand to a size on the order of the particle radius.

Aspelmeyer’s long-term vision is to apply his technique to particles that are large enough to produce a measurable gravitational field. In that regime, questions about how the gravitational field looks for an expanded wavepacket can be answered. But Aspelmeyer says those experiments are still a decade or two away.