A tiny swimmer generates rapid, far-reaching signals in water

In flocks of birds, schools of fish, and colonies of bacteria, individuals can interact in ways that benefit the group. Advantages conferred by working together may include better protection against predators, greater ease of foraging, and more efficient locomotion. Group behavior in many species arises from cascading signals transmitted by individuals. Understanding how signaling works across the natural world not only provides insights into biodiversity, but also helps engineers design groups of robots that autonomously coordinate movements in challenging environments.

Large aquatic organisms are well equipped for communication. Sensory tools including sight, sound, and smell offer possibilities for transmitting signals between distant neighbors. Microscopic swimmers lack complex sensory channels. For them, signaling may take the form of flows generated by swimming. An individual may sense the movement of fluid from a neighbor and adjust its behavior. (See the article by Eric Lauga and Raymond Goldstein, Physics Today, September 2012, page 30 .) But hydrodynamic signals generally decay with distance and only transmit information among individuals that are already close together. Some bacteria congregate into groups of 10⁸ cells per cubic centimeter to coordinate their movements via hydrodynamic signals. Active cellular communication within a fluid may also entail a single cell swimming to deliver a signal to another cell, so messages only travel as fast as the cell can swim.

In a pond in California’s Bay Area, single-celled Spirostomum ambiguum has found a way to generate eddies that travel orders of magnitude faster than the organism can swim. By observing the creature’s quirky movements, Arnold Mathijssen and Manu Prakash from Stanford University, along with Joshua Culver and Saad Bhamla of Georgia Tech, discovered a new form of rapid, long-range signaling between single-celled organisms. ¹

The ultrafast hero

The Baylands Nature Preserve in Palo Alto, the background in figure 1, has proven to be a reliable source of fast-moving microswimmers, ideal for the team’s ongoing investigation into single cells’ power output capacities. One day, on peering at the brackish waters through a hand-made, pocket-sized microscope, Prakash noticed a tiny creature that contracted its body so rapidly that it seemed to disappear.

Figure 1.

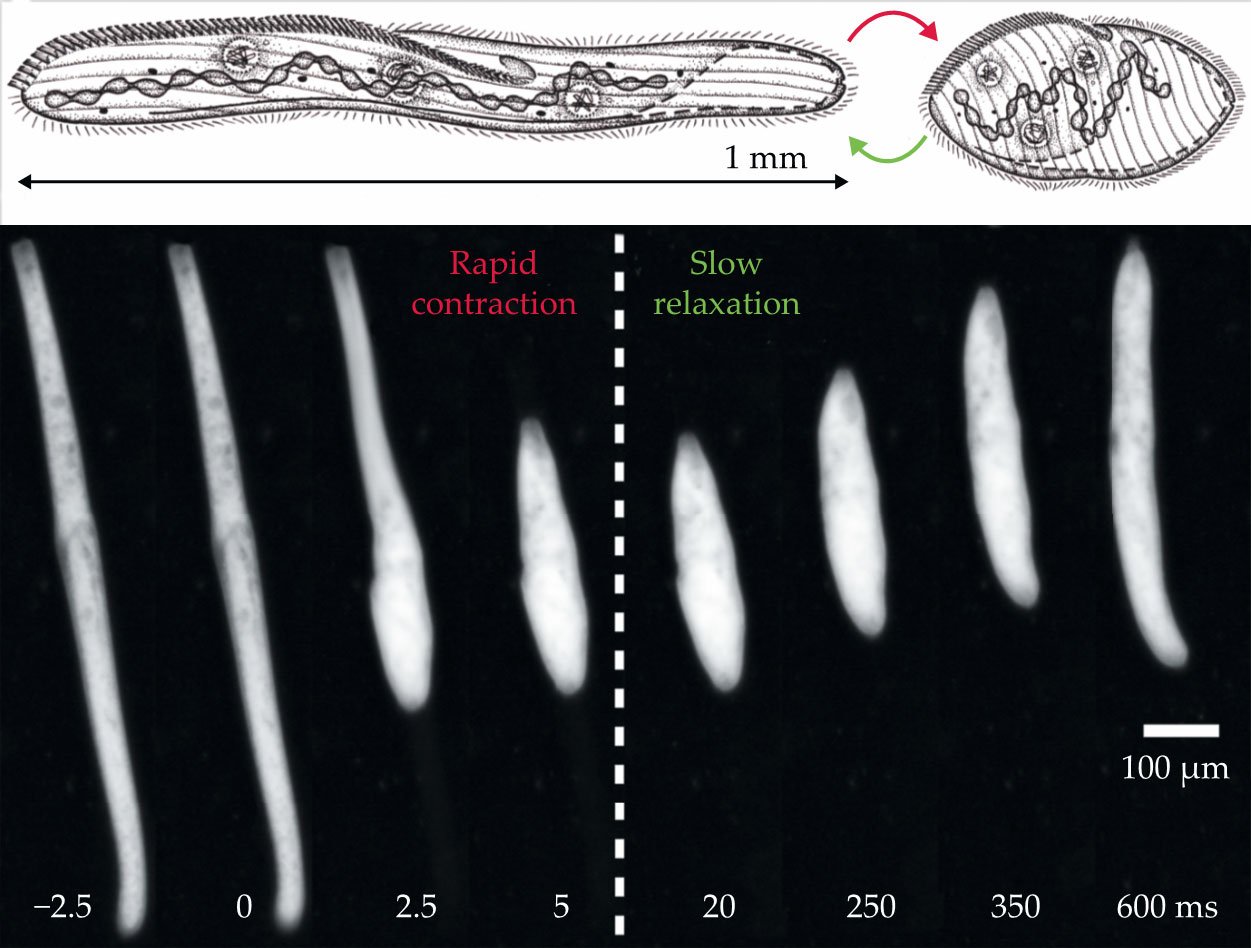
Prakash was not the first to notice Spirostomum ambiguum. The marsh-dwelling creature has attracted biologists’ attention ² since 1873. At 1 mm to 4 mm long, S. ambiguum is exceptionally large for a single-celled organism. It can shorten its body in an extremely rapid contraction and shrink to less than half its normal size in just 5 ms. After contracting, the organism relaxes to its full length over a leisurely 1 s, shown in figure 2. During contraction, the cell endures an acceleration 14 times the force of gravity (14g). An airplane that accelerates at more than 12g is illegal in some aerobatics races because of danger to the pilot.

Figure 2.

The Stanford researchers collected water samples containing S. ambiguum to investigate its extraordinary behavior. They wanted to find out why the creature evolved the ability to contract so rapidly and how it did so without damaging its internal structures. When Bhamla (formerly a postdoc in Prakash’s lab and now an assistant professor at Georgia Tech) started to grow cultures of the creature in the lab, he found a surprise. The cells assembled into clusters and appeared to contract together, sending a pulse of motion through the colony. “This was an exciting and serendipitous discovery,” Bhamla recalls.

Stirring things up

To learn more about S. ambiguum’s behavior, Mathijssen (a postdoc in Prakash’s lab) adapted a colleague’s earlier experiment designed to investigate how an individual cell senses the movement of water around it. He and Bhamla stimulated a single S. ambiguum with gentle electrical pulses that caused it to contract, and they used micron-scale plastic beads to visualize the resulting flow fields around it. By observing the beads with a high-speed video camera, they found that a single cell’s contraction generated a turbulent flow in the surrounding fluid.

The smaller a swimmer is, the more it has to accelerate to generate turbulence. ³ The characteristic flow around any swimmer is dictated by the relative importance of viscous and inertial forces on the fluid’s motion, a ratio described by the dimensionless Reynolds number Re. A large swimmer in water, like a human, swims at a high Reynolds number (Re ~ 10⁵). The viscous forces are negligible, and the swimmer’s motion easily churns up eddies. A tiny swimmer, like S. ambiguum, swims at a low Reynolds number (Re ~ 0.1). Viscous forces dominate, and the swimmer’s motion is unlikely to impart enough force to stir up the water. ⁴ But when S. ambiguum contracts, it accelerates enough to overcome the viscous effects of the water and generate a turbulent flow. In those milliseconds, the Reynolds number surges to 50.

To investigate what advantage generating a turbulent flow provides S. ambiguum, Mathijssen and Bhamla first sought to identify the mechanism that triggers the creature’s contraction. Zoologists had posited that an individual S. ambiguum contracts when it senses a change in its surroundings, perhaps the presence of a freshwater flatworm or other predator. The Stanford researchers designed an experiment that mimicked the sucking motion of a predator’s filter-feeding action. They suctioned liquid out of a small hole in a pair of slides containing a single S. ambiguum in water. As the suction drew the cell closer to the hole, its body became stretched. The cell contracted when it reached a critical strain threshold.

The strain required to trigger contraction matched the threshold for opening ion channels commonly found on a cell’s outer membrane. ⁵ Once the channels are open, ions can enter the cell and engage filaments that make the cell contract—a common situation in other organisms, though biologists have not directly observed it in S. ambiguum.

An aquatic game of telephone

The observation that fluid flow triggers the cell’s contraction suggested that S. ambiguum can both generate and read hydrodynamic signals. Prakash says, “That was the ‘aha’ moment!” The team’s calculations showed that the turbulent flow produced by a contracting cell could generate a contraction-inducing strain in a neighbor up to a millimeter away.

To test the theory that S. ambiguum relies on hydrodynamic flows for communication, Mathijssen and grad student Culver investigated cells gathered in close proximity. If a cell felt an impulsive, turbulent flow, it would contract and generate its own turbulent flow, which would in turn cause other cells to contract. A hydrodynamic wave propagated through clustered cells at 0.25 m/s, hundreds of times faster than the cells’ normal swimming speed of 0.2 mm/s. Figure 3 shows a wave of contractions propagating through a colony of cells.

Figure 3.

Mathijssen proposed that a critical population density of cells allows the hydrodynamic signal to propagate throughout the colony. Below that density, the signal does not reach the entire network. Percolation theory—how information spreads throughout a network based on size, shape, and orientation of interacting nodes—suggests that at about 2 individuals per square millimeter, the signal propagates in a fractal path and quickly reaches the edge of the colony. Below that density, the signal dies out. Above it, the signal spreads radially from the first cell but travels at a slower velocity.

The authors proposed a possible functionality for the colony’s collective contraction. When subjected to mechanical or electrical stimulation, ⁶ S. ambiguum releases toxins from pockets fixed to the cell membrane. The researchers found that the organism releases the toxin at the exact moment that it contracts. The vortex flow generated by contraction transports the toxin rapidly into the surrounding medium, faster than the toxin can diffuse on its own.

The results suggest that coordinated contractions may help the colony avoid danger. Flows generated by a large predator may prompt an individual to contract and signal its neighbors to do so as well. Synchronized toxin release may help the colony deter multicellular predators like the flatworm Stenostomum sphagnetorum, which learns to avoid the elusive prey.