A powerful quantum chemical method tackles a protein

The fundamentals of theoretical chemistry are straightforward. A molecule’s electrons and atomic nuclei interact via a Coulomb potential. Nuclei can usually be treated as stationary classical particles, and electrons can often be assumed to be nonrelativistic. Solving the Schrödinger equation thus yields a molecule’s electronic structure and energy, from which one can derive reaction energies, spectroscopic properties, and other aspects of chemical behavior.

But the many-electron Schrödinger equation is too difficult to solve exactly. Computational chemists must develop simplifications that sacrifice some accuracy for the sake of efficiency. One approach, suitable for especially large or dynamic systems, is to treat just part of the molecule quantum mechanically and to simulate the rest classically. For their pioneering work on those quantum–classical hybrid models, Martin Karplus, Michael Levitt, and Arieh Warshel were awarded the 2013 Nobel Prize in Chemistry, which will be covered in detail in the December issue of Physics Today.

Even when the entire system must be treated quantum mechanically, some approximations can still be made. (See the article by Martin Head-Gordon and Emilio Artacho, Physics Today, April 2008, page 58 .) One favorite approximation, coupled-cluster theory, is regarded as the gold standard for computational chemistry: It can compute relative energies to within 0.04 eV—accurate enough for most purposes—using just a tiny fraction of the computing time required for an exact solution. ¹ But for large molecules, standard coupled-cluster theory is still far too computationally intense; one must typically resort to less accurate methods.

Frank Neese and colleagues at the Max Planck Institute for Chemical Energy Conversion have now developed an approach to coupled-cluster theory that reduces the difficulty of the calculation by a factor of 10⁶ or more, while sacrificing little accuracy. ^{2 , 3} With it, they can compute coupled-cluster energies of molecules with several hundred atoms in a matter of days or weeks. Standard coupled-cluster calculations on the same molecules would take many thousands or even millions of years.

Hartree–Fock

The simplest useful computational chemistry method, and the one on which many others are based, is the Hartree–Fock method. In Hartree–Fock’s predecessor, the Hartree method, the N-electron wavefunction Ψ is approximated as the direct product of N single-electron wavefunctions, or orbitals, φ_i: Ψ(x₁, x₂, … x_N) = φ₁(x₁)φ₂(x₂) … φ_N(x_N), where x_i is the spatial position of the ith electron. The molecular orbitals φ_i are solved self-consistently: Each electron feels the electric field of all the other electrons, averaged over their respective wavefunctions. In modern implementations of the Hartree and other methods, the φ_i are written as linear combinations of a finite, predetermined set of basis functions, usually based on atomic orbitals. One aims to choose a basis that is large enough to be reasonably complete.

The Hartree method accounts for electron–electron repulsion in a rudimentary way. But in the true N-electron wavefunction, the electron positions are correlated in a way that can never be reproduced by the product of N single-electron wavefunctions. For one thing, electrons are identical fermions, no two of which can be in the same place at the same time. The Hartree–Fock method improves on the Hartree method by antisymmetrizing the wavefunction to account for the electrons’ Fermi statistics. For a two-electron system, the Hartree–Fock wavefunction is proportional to φ₁(x₁)φ₂(x₂) − φ₂(x₁)φ₁(x₂), and so on for larger systems; the overall form is known as a Slater determinant.

But that’s not good enough. Hartree–Fock still neglects the correlations that arise from Coulomb repulsion, and thus its predictions are often qualitatively incorrect. Recovering that remaining electron correlation—and more specifically, the correlation energy, defined as the difference between the exact energy and the best Hartree–Fock energy—is a major goal of computational methods such as those described below.

Coupled cluster

One way to improve on Hartree–Fock is to write the wavefunction as a linear combination of the Hartree–Fock, or “reference,” Slater determinant and similar Slater determinants with one or more of the electrons promoted into higher-energy orbitals, as shown in figure 1. Within that space of linear combinations, one then optimizes the coefficient of each Slater determinant to find the lowest-energy eigenstate of the molecular Hamiltonian.

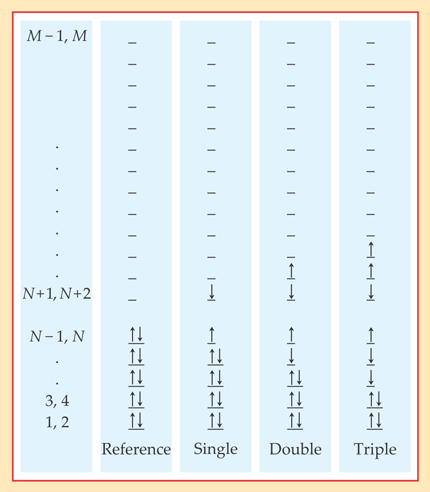
Because the excited orbitals, like the Hartree orbitals, are linear combinations of a finite number of basis functions, their total number M is finite. So in principle it’s possible to consider all M!/N!(M − N)! of the possible excited Slater determinants. That approach, called the full configuration interaction (CI) method, gives the exact solution within the constraints of the original basis set. But its computational intensity grows exponentially with N, so it’s not practical for any but the very smallest systems.

Coupled-cluster theory approximates the full CI method by reducing the number of coefficients to be optimized. For example, in CCSD (for “coupled-cluster singles doubles”), only the one- and two-electron excitations have their own coefficients. The coupled-cluster wavefunction is no longer a simple linear combination of its constituent Slater determinants, so higher-order excitations aren’t left out; instead, they’re expressed in terms of one- and two-electron excitations. That approach treats two-electron correlations exactly and scales in intensity like N⁶, but it’s not quite accurate enough for chemical purposes. Adding a perturbative correction for triple excitations yields CCSD(T), which achieves chemical accuracy with N⁷ scaling.

That’s far better than the exponential scaling of the full CI. But CCSD(T) is still too slow to use on molecules with more than about a dozen atoms. And even as computers get faster and more powerful, it will take a 128-fold increase in speed to allow just a twofold increase in system size.

Linear scaling

There should be a way to do better. Electron correlation has long been recognized to be local: The correlations in one part of a molecule don’t significantly depend on those in another. It ought, therefore, to be possible to break up a molecule into segments and calculate the correlation energy of each—with the overall calculation scaling linearly, like N. But how to implement such a calculation is far from obvious.

Rather than chopping up the molecule in real space, Neese and colleagues approach the problem by compressing information in orbital space. In 2009 they turned to the decades-old concept of pair natural orbitals (PNOs): For each electron pair, one transforms the space of excited molecular orbitals so as to capture that pair’s contribution to the correlation energy in as few orbitals as possible.

By truncating the wavefunction expansion to include only those PNOs that are expected to significantly contribute, Neese and colleagues drastically reduced the complexity of a coupled-cluster calculation. ⁴ But calculating all of the PNOs took time. In the end, the PNO-based methods were a big improvement over standard coupled-cluster methods, but their scaling was nowhere near linear.

Over the past two years, Neese had his postdoc Christoph Riplinger (now at Princeton University) look for a faster method for calculating the PNOs. Inspired by Hans-Joachim Werner and colleagues’ success ⁵ in representing excited orbitals as sums of local projected atomic orbitals ⁶ (PAOs), Riplinger developed a way to expand the PNOs in terms of PAOs. “Getting the integral transformations to scale linearly was an incredibly difficult bookkeeping problem,” explains Neese. “Christoph was able to look far enough ahead into the calculation to figure out which integral is needed when and where—and why.”

Furthermore, Neese developed an efficient way of prescreening electron pairs to exclude those whose excitations don’t significantly contribute to the correlation at all, thereby reducing the complexity of the calculation by as much as 90%. Technically, any process that considers electrons two at a time must scale at least like N². But the prescreening was a small enough part of the whole calculation that the overall method scales almost like N.

Earlier this year Riplinger and Neese presented their nearly linear method for CCSD, ² which they’ve dubbed “domain-based local PNO-CCSD.” And now they and their colleagues have applied the same methods to the perturbative triples correction, resulting in DLPNO-CCSD(T). ³

Large molecules

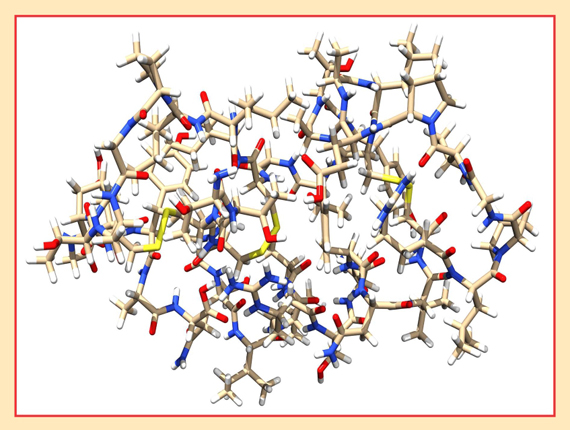
Even with all the approximations and truncations made by DLPNO-CCSD(T), the researchers found that it still captures more than 99.8% of the standard CCSD(T) correlation energy for a test set of medium-sized organic molecules. And they were able to calculate coupled-cluster energies for far larger molecules than had ever been possible before, including the linear hydrocarbon C₁₅₀H₃₀₂ and the 644-atom protein crambin, shown in figure 2. “I was remembering that a few years back, Filipp Furche and John Perdew presented a calculation on the crambin molecule using RI-DFT,” says Neese, referring to resolution of the identity density-functional theory, the most efficient DFT method. ⁷ “That was a spectacular calculation in 2006.” By working with the three-dimensional electron density rather than the 3N-dimensional N-electron wavefunction, DFT has a natural efficiency advantage over wavefunction methods, so it’s often the approach of choice for studying large molecules. But its accuracy has yet to rival that of CCSD(T).

Neese and colleagues are continuing to work toward making their DLPNO-based coupled-cluster methods as useful as possible for users’ calculations. For example, they hope to develop a code to treat molecules such as ozone, which aren’t easily studied with coupled-cluster theory because they have unpaired electrons and aren’t well approximated by a single reference state. They plan to make all their methods available to users via their software package ORCA.