A powerful interferometer works by holding, not dropping, its atoms

Photons and atoms are both described by a wavefunction, whose phase defines a natural ruler that can be used for measuring fields and forces. But when made ultracold, atoms can offer far greater precision. They also have gravitational signals imprinted on their interference pattern, which can resolve changes in Earth’s gravity to one part in 10¹¹. That’s sensitive enough to detect such features as oil wells, caves, and tunnels; changes in the local water table; and glacial melting. (See the article by Markus Arndt, Physics Today, May 2014, page 30 .)

Conventional atom interferometers measure gravity by throwing atoms upward and watching them fall. Light pulses tuned to particular resonance frequencies in the atoms serve as beamsplitters and mirrors. The pulses deliver momentum kicks that split the atoms into two wavepackets, send them along separate paths, and then recombine them. At a detection port, the matter waves interfere according to the phase difference between the kicked and unkicked wavepackets—the two arms of the interferometer.

But that approach has two related limitations. An atomic fountain takes up a lot of space—the atoms are launched to a height of several meters in a vacuum. Even with such heights, the duration of the atoms’ free fall, which determines the interferometer’s sensitivity, lasts only a few seconds. In 2013 Stanford University’s Mark Kasevich and collaborators reached a milestone, obtaining 2.3 seconds of interrogation time using a 10-meter fountain. ¹ Work is now underway to build fountains measuring up to 300 m. But their sensitivity to vibrations, exacerbated by the increased height, requires elaborate inertial stabilization.

Holger Müller and his group (shown in figure 1) at the University of California, Berkeley, have now demonstrated an alternative method ² that extends the interrogation time to as long as 20 seconds—the longest coherence time ever obtained for a spatially separated quantum superposition. The achievement came from holding the two wavepackets in an optical lattice after the matter waves were split and separated by light pulses. Without the lattice to hold the atoms against gravity, interrogating them for that long in free fall would require a vacuum system a half kilometer tall.

Figure 1.

The Berkeley system takes just 1 meter of vertical space in the researchers’ lab. The compact geometry makes it attractive for a mobile atomic gravimeter that can take data in the field. Indeed, Müller already has a project planned to place the system on a drone.

An optical lattice in an optical cavity

A schematic of the new interferometer is shown in figure 2. To make a gravity measurement, the researchers launch a cloud of cesium atoms chilled to 300 nK upward a few millimeters into the center of an optical cavity. As in conventional interferometers, the atoms can be steered in free fall by using Raman transitions: Two counterpropagating laser beams, whose frequency difference corresponds to a hyperfine transition, irradiate the atoms and transfer momentum to them, with each pulse’s intensity tuned to kick the atoms with 50% probability.

Figure 2.

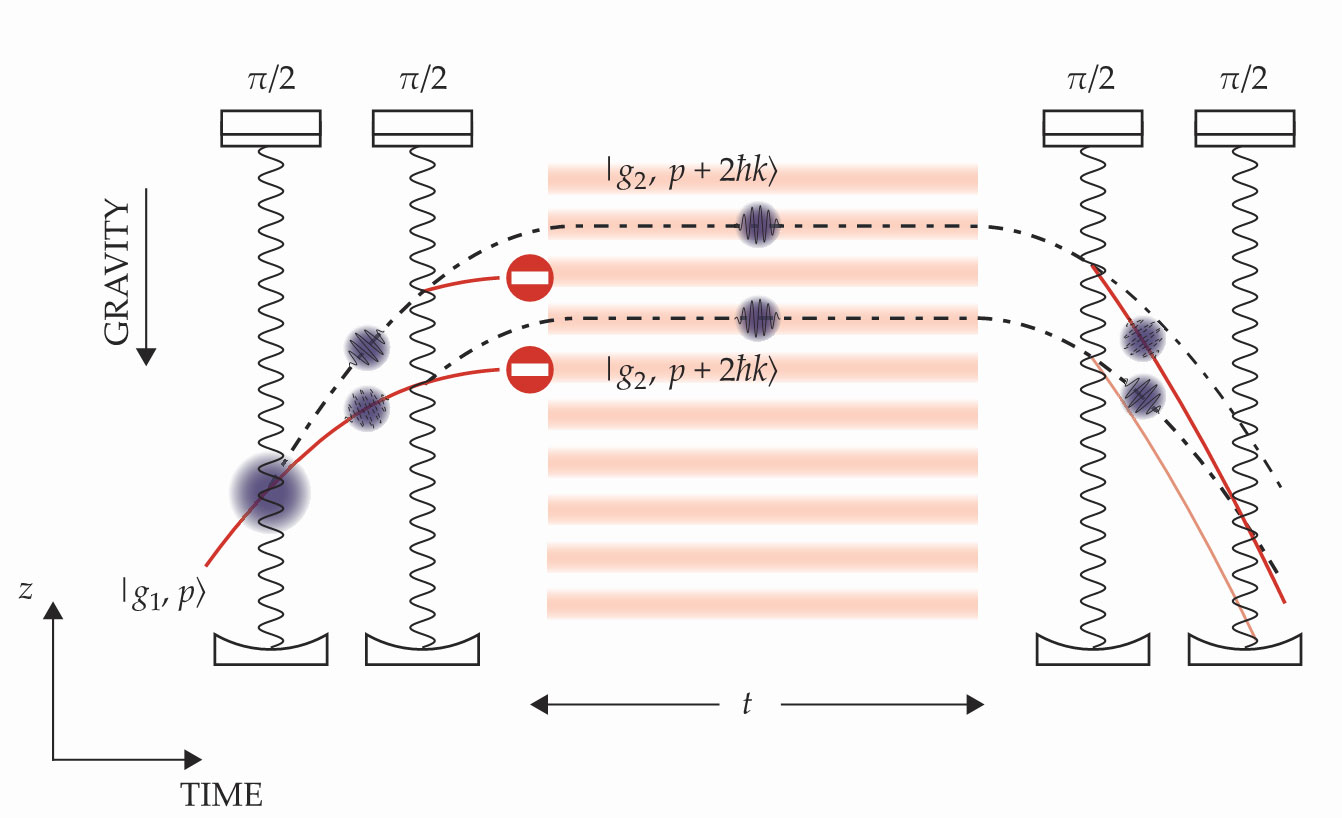
Four of those π/2 pulses accompany the atom cloud through the interferometer. The first pulse places each Cs atom into a coherent superposition of two states—one that receives a momentum kick and one that doesn’t. The two clouds form localized partial wavepackets traveling along distinct trajectories at different momenta, and the two trajectories form the upper and lower arms of the interferometer.

The second pulse provides another kick, designed to rematch the wavepackets’ momenta as they continue rising. At their apex, an optical lattice is turned on to suspend the wavepackets in vacuum. In the lattice, only the two wavepackets’ different heights and thus potential-energy difference in the gravitational field distinguish them. After a time t, a second pair of π/2 pulses steers the wavepackets so that they can interfere according to the phase difference accumulated between the upper and lower arms.

Placing a vertical optical lattice inside an atom interferometer isn’t new. Yannick Bidel, now at the French aerospace lab ONERA, and coworkers built nearly the same configuration in 2012. So did Guglielmo Tino and his group four years later at the University of Florence. In both cases the optical lattice trapped the clouds of cold atoms, but imperfections in the free-space laser beams limited the interrogation times to just 0.1 seconds and 1.0 second, respectively. ³

What makes the experiment so challenging—and the newly achieved 20-second hold time so astonishing—is that the trapping potential must be strong enough to overcome gravity but gentle enough to preserve the atoms’ de Broglie–wave phase. Says NSF program director Alex Cronin, “Before this demonstration, I was skeptical that an atom interferometer could ever work with traps turning on and off in the middle of it.” The trap has to grab the spatially separated components of each atom’s wavefunction without ever changing its quantum state. “Catching matter waves midflight without scrambling their coherence is an exquisite example of quantum mechanical engineering,” he says.

Even at 300 nK, the atoms shake in the antinodes of the standing waves that hold them. To minimize the light scattering and avoid exciting any atoms above the ground state, the researchers detuned the frequency of their trapping lasers to 866 nm, far from any of the atoms’ transition frequencies. Even so, a realistic laser beam can never generate an optical lattice with perfect translational invariance. To solve that problem they incorporated a key feature in their setup—an optical cavity that bounds the optical lattice between two highly reflective mirrors.

The marriage between atom interferometry and cavity optics was made four years ago by Müller, his then postdoc Paul Hamilton (now at UCLA), and his current postdoc Matt Jaffe ⁴ (see Physics Today, April 2015, page 12 ), and the cavity’s presence is paramount for achieving long coherence times. For one thing, the cavity mirrors spatially filter the trapping light because only the fundamental Gaussian mode of the cavity is resonant with it. The hundred or so reflections between the mirrors reinforce that mode and improve the uniformity of the optical traps. They also suppress the effect of laser speckle, mirror dust, and any other inhomogeneities in the laser’s wavefront.

What’s more, the reflections enhance the power of laser light in the cavity by some 40-fold. Years earlier the enhancement led to the group’s discovery that gravity measurements could be made at a precision comparable to that of conventional atom interferometers but with far less power—milliwatts instead of watts. The lower power demand helps keep the system compact and reduces stray light generated at external lenses and mirrors that could otherwise distort the lattice sites.

Toward state of the art

Being able to sustain the coherence of the wavepackets for long times confers another advantage to the new interferometer: vibration suppression. Whereas atomic fountains measure the wavepackets’ phase at just three positions—at the beginning of their trajectory, at their apex, and when they interfere—the Berkeley interferometer integrates the phase continuously as long as the atoms are suspended in the lattice.

The longer the hold time, the more the vibrations average out. The 20 seconds that Müller achieved reduces the interferometer’s phase sensitivity to vibrations by up to four orders of magnitude. He was surprised to discover that as the lattice hold times kept increasing, his team stopped needing any vibration isolation.

Despite its advantages, the new device still falls short of state-of-the-art atom interferometers. In the Berkeley group’s proof-of-principle demonstration, the gravitational potential-energy difference from just 4 µm of vertical separation generates 1.6 megaradians of phase accumulated in the two arms. But there’s room to improve that performance. An interferometer’s precision increases with both longer hold times and larger wavepacket separations.

The 4 µm separation between the arms was achieved using the momentum kick from just a single two-photon Raman transition. In a separate experiment, Müller and coworkers have demonstrated laser pulses strong enough to generate 10-photon momentum kicks and almost 9 mm of separation. No fundamental barrier limits increasing the separation and hold times, but maintaining the coherence of such large spatial superpositions remains a huge technical challenge.

The compact nature of the new interferometer makes it ideal for measuring short-ranged interactions, such as Casimir forces and those hypothesized to be responsible for dark energy. And the different nature of the new approach—holding atoms to probe the potential-energy difference rather than dropping them to measure accelerations—has Müller particularly intrigued.

Measuring the phase of atoms from different gravitational potentials but in a gravitational-force-free setting—for example, inside a spherical shell of uniform mass—would be tantamount to observing the gravitational analogue of the Aharonov–Bohm effect. The experiment, which Müller proposed with the University of Vienna’s Anton Zeilinger in 2012, would constitute the first demonstration of a force-free gravitational redshift. ⁵ It would also provide a new measurement of Newton’s constant G, the least accurately known fundamental constant in nature.