A new upper limit on the electron’s electric dipole moment

Shortly after the 1957 discovery that mirror symmetry (conservation of parity P) is violated in the weak interactions, Edward Purcell and Norman Ramsey devised an experiment to look for a nonzero electric dipole moment (EDM) in the neutron—which P conservation would have forbidden. They found none, but they were able to set an upper limit of 5 × 10⁻²⁰e·cm on its magnitude—impressively small with the available technology.

That null result would have come as a relief to theorists of the day. Though P conservation had been overthrown, it was believed that the combination CP was still a good symmetry operation (C being the replacement of particles by their antiparticles). That is, particles were presumed always to behave like their antiparticles viewed in a mirror. And CP conservation itself forbids an EDM for any elementary particle.

Seven years later, however, CP conservation was found to be violated in the decay of neutral K mesons. The standard model of particle physics that developed over the next 20 years incorporates a mechanism for CP violation, and indeed it predicts a nonzero EDM for the electron. But its predicted magnitude, less than 10⁻³⁸e·cm, is far too small to detect by any technique in the foreseeable future.

And yet, a dozen experimental teams worldwide are currently searching for the electron’s EDM. That’s because the standard model is manifestly incomplete, and most of the leading candidate theories for new physics beyond its purview predict electron EDMs just big enough to detect with current frontier techniques. Furthermore, new CP-violating mechanisms are needed to explain the cosmic matter–antimatter imbalance (see the article by Helen Quinn in PHYSICS TODAY, February 2003, page 30 ). Some experimenters argue that the search for the electron’s EDM might be the fastest road to the new physics.

An electron EDM vector d_e would manifest itself as a tiny energy split 2d_eE between states in which the electron’s spin (which must be colinear with d_e) is parallel and antiparallel to an applied electric field E. But one can’t simply expose a free electron to an electric field; the field would sweep it away. That’s why the experimenters look at unpaired electrons inside neutral atoms or molecules subjected to an external field.

The new upper limit

No one has as yet found evidence of a nonzero d_e. Until this year, the tightest upper limit had been reported in 2002 by Eugene Commins’s group at the University of California, Berkeley. ¹ Using a beam of thallium atoms, they found that d_e does not exceed 2 × 10⁻²⁷e·cm. That limit already began to encroach on the parameter space of a popular theoretical candidate, the minimal supersymmetric model. But the Berkeley experiment is now seen as the high-water mark of the atomic-beam technique. Systematic uncertainties inherent in that technique have led experimenters to seek alternative ways of searching for d_e.

Now Edward Hinds’s group at Imperial College London, using a beam of cold polar molecules, has achieved the first improvement on the Berkeley upper limit.² The new limit of 1 × 10⁻²⁷e·cm thus far only doubles the sensitivity of the old experiment, but it’s regarded as the proof-of-principle demonstration of a demanding technology that experimenters have been struggling with for a decade. The IC team’s result is still limited by statistical noise rather than systematics.

In atoms and molecules with heavy nuclei, a relativistic effect of polarization in an applied electric field E can subject an unpaired electron to a much stronger effective field E_eff in the same direction. That amplification is particularly strong in polar diatomic molecules like ytterbium fluoride, the species chosen by the IC team. In the experiment, an applied field of 10 kV/cm subjects the molecule’s lone unpaired electron to an E_eff a million times stronger. Even so, the team faces the exacting task of looking for an EDM energy split of a few attoelectron volts (10⁻¹⁸ eV). And the aggressive chemical reactivity of suitable molecules like YbF restricts the experiment to much lower beam densities than one can get with atomic beams.

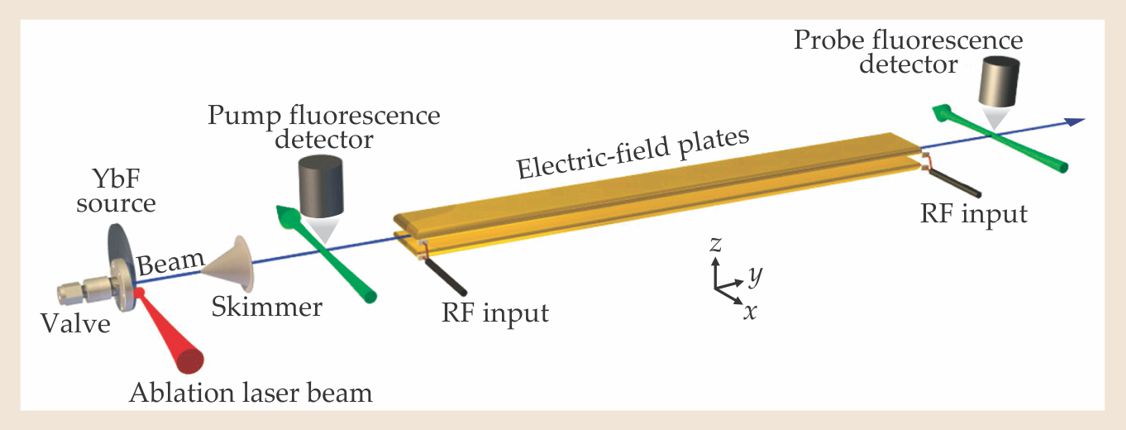
Hinds and company seek to detect the EDM energy split by observing quantum interference between hyperfine levels of the YbF molecule’s ground state. The Yb nucleus being spinless, the spin-1⁄2 fluorine nucleus combines with the molecule’s unpaired electron spin to form hyperfine states of total spin F = 0 and 1, separated by about a microelectron volt. In the absence of external electric or magnetic fields, the three orientational substates of the F = 1 state are degenerate. But in the IC experiment, the beam runs between field plates that subject it to E and B fields normal to the plates (see figure 1). Either field can be reversed at will.

In those external fields, the up and down spin substates F_z = +1 and –1 are separated in energy by

ΔH = 2(μ_BB ∓ d_eE_eff),

depending on the sign of E · B. In the familiar first (Zeeman splitting) term, μ_B is the Bohr magneton. Even with the experiment’s submilligauss B field (painstakingly shielded from the geomagnetic and stray fields), the Zeeman term is overwhelmingly larger than the putative second (EDM) term the team hopes eventually to discern. So their strategy is constantly to reverse either field at random and search for correlations between small, noisy fluctuations and the sign of E · B.

A quantum interferometer

The interferometer is the pulsed-molecular-beam setup shown in figure 1. Every 40 milliseconds, Yb atoms laser-ablated from a solid source encounter a pulse of fluoride gas to form some YbF. Those molecules, entrained in argon carrier gas that has been cooled to 3 K by free expansion through a valve, form an almost monoenergetic YbF beam. At that point, the YbF population is an incoherent mix of the F = 0 and 1 hyperfine levels.

Before the YbF pulse enters the 75-cm-long region between the field plates that will subject it to the E and B fields, it’s hit with a “pump” laser pulse tuned to excite all the F = 1 molecules and thus effectively leave behind a pure F = 0 beam to initialize the interferometry. But the discarded F = 1 population also serves a purpose; the strength of its fluorescence signal as it de-excites provides a normalizing measure of the initial YbF population, which varies from pulse to pulse.

As the pulsed beam enters the field region between the plates, it’s irradiated with an RF pulse whose frequency and duration are precisely chosen to raise the molecules from the hyperfine state ∣F,F_z〉 = ∣0,0〉 to the coherent initial superposition state

∣ψ_i〉 = (∣1,+1〉 + ∣1,–1〉)/√2.

Then, as the molecules traverse the field region, the resultant energy difference between the wavefunction’s up and down components creates a growing phase difference θ(t) = tΔH/ℏ between them, where t is the travel time through the fields.

If, for example, θ is an odd multiple of π at the end of the field region, the hyperfine state will have evolved into (∣1,+1〉 − ∣1,–1〉)/√2, orthogonal to ∣ψ_i〉. Whatever the final state ∣ψ_f〉 at the downstream end, it encounters a second RF pulse identical to the first one. The second pulse, however, sends the ∣ψ_i〉 component of ∣ψ_f〉—but only that component—back down to ∣0,0〉.

So the population of molecules emerging from the field plates with F = 0 is proportional to ∣〈ψ_i∣ψ_f〉∣² = cos²(θ/2). Finally that population fraction, which depends ever so slightly on d_e, is measured by subjecting the emerging bunch to a “probe” laser beam tuned to excite only F = 0 molecules to fluorescence, and then normalizing that fluorescence signal to the pump fluorescence signal.

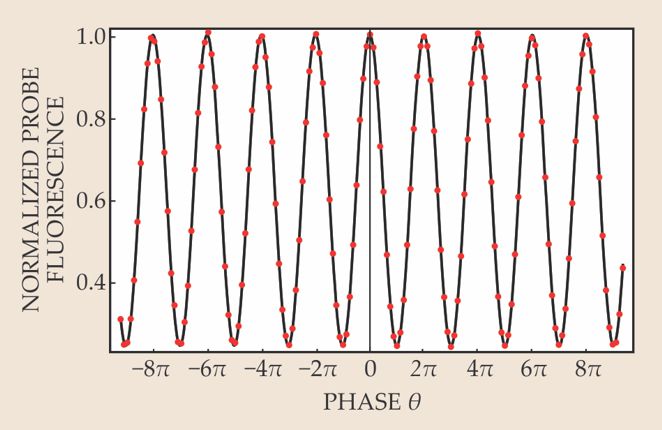
Figure 2 shows the interference pattern imposed on the normalized fluorescence signal by scanning B in 45-µG steps, while E is held fixed at about 10 kV/cm. In the EDM search, B is mostly set in the vicinity of ±136 µG, where the central interference fringe is steepest and therefore most sensitive to small EDM-induced shifts when fields are reversed. The fields are generally reversed randomly from pulse to pulse by computer-controlled switches. But additionally, the RF, high-voltage, and magnet-coil cables are manually reversed every few days to ferret out systematic errors.

Implications of a null result

The IC team’s published d_e limit is based on 25 million pulses. To derive a d_e from apparent correlations between fluorescence signals and field directions, the team had to invoke a relativistic molecular-physics calculation of E_eff in YbF as a function of the applied E. Figure 3 shows separately the d_e values measured with each of the experiment’s eight different cabling arrangements. Clearly, they’re all consistent with each other and with d_e = 0.

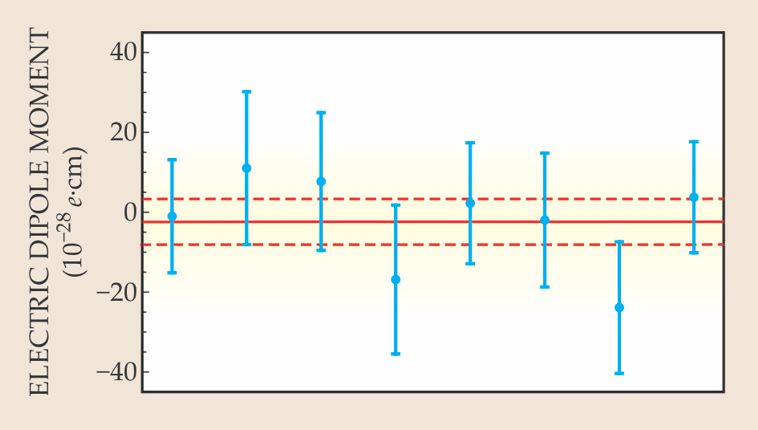
The overall result, d_e = (−2.4 ± 5.9) × 10⁻²⁸ e·cm, with the uncertainty dominated by statistics, translates into a 90%-confidence limit of 1.05 × 10⁻²⁷e·cm on the moment’s magnitude. A statistically significant negative d_e would mean that the electron’s spin is antiparallel to its electric dipole moment.

As Hinds and company continue their quest for a nonzero d_e, they’re introducing a truly cryogenic beam source rather than continuing to rely on free-expansion cooling. “By increasing the beam’s travel time and its intensity,” says Hinds, “the colder source should increase our sensitivity by an order of magnitude within a few years.”

Other groups are developing experiments with molecules whose more complex energy-level schemes should make it easier to distinguish true EDM signals from magnetic artifacts. And some groups are revisiting heavy atoms. But nowadays the idea is to immobilize them in optical lattices so as to avoid spurious magnetic effects due to weakly polarized atoms speeding across the applied electric field—effects that capped the sensitivity of atomic-beam searches a decade ago.

The big accelerators are searching—thus far without a sighting—for the heavy supersymmetric (SUSY) particles predicted by the most popular extensions of the standard model. The lightest of them shouldn’t be much heavier than 1 TeV if supersymmetry is to serve its principal purpose of reconciling the observed sub-TeV energy scale of electroweak-symmetry breaking with the 10¹⁶-TeV Planck scale.

For the minimal supersymmetric model, however, the new d_e limit already precludes SUSY particles lighter than 4 TeV—unless the model’s free CP-violating parameter is improbably small. “So by looking for an attoelectron-volt energy splitting in a cold-molecule laboratory,” says Hinds, “we’re learning something about nature on the teraelectron-volt scale.”